Skip to main content
SpringerLink
Log in

Direct Operational Vector Scheme for First-Kind Nonlinear Volterra Integral Equations and Its Convergence Analysis

  • Published:
Mediterranean Journal of Mathematics Aims and scope Submit manuscript

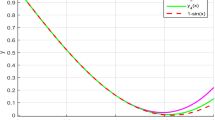
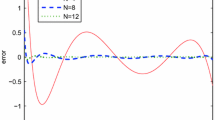
Abstract

In the current paper, an efficient direct numerical scheme is developed to approximate the solution of nonlinear Volterra integral equations of the first kind. This computational method is based upon operational matrices and vectors which eventually lead to the sparsity of the coefficients matrix of the obtained system. For this purpose, the operational vector for hybrid block pulse functions and Chebyshev polynomials is constructed. Hybrid functions are powerful tools to approximate functions locally, and capable to adjust the orders of block-pulse functions and Chebyshev polynomials to achieve highly accurate numerical solutions. Its simple structure to implement, low computational cost and perfect approximate solutions are the major points of the presented method. The convergence analysis of the numerical approach under the \(L^2\)-norm is completely studied. Finally, numerical experiments indicate that the proposed approach is effective and powerful to deal with smooth and non-smooth solutions and verify the obtained theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Atkinson, K.E.: The numerical solution of integral equations of the second kind. Cambridge University Press, New York (1997)

    Book  Google Scholar 

  2. Atkinson, K., Han, W.: Theoretical numerical analysis, third ed., vol. 39 of Texts in Applied Mathematics. Springer, Dordrecht, A functional analysis framework (2009)

  3. Babolian, E., Masouri, Z.: Direct method to solve Volterra integral equation of the first kind using operational matrix with block-pulse functions. J. Comput. Appl. Math. 220, 51–57 (2008)

    Article  MathSciNet  Google Scholar 

  4. Babolian, E., Salimi Shamloo, A.: Numerical solution of Volterra integral and integro-differential equation of convolution type by using operational matrices of piecewise constant orthogonal functions. J. Comput. Appl. Math. 214, 495–508 (2008)

    Article  MathSciNet  Google Scholar 

  5. Babolian, E., Maleknejad, K., Mordad, M., Rahimi, B.: A numerical method for solving Fredholm-Volterra integral equations in two-dimensional spaces using block pulse functions and an operational matrix. J. Comput. Appl. Math. 235(14), 3965–3971 (2011)

    Article  MathSciNet  Google Scholar 

  6. Bartoshevich, M.A.: On one heat conduction problem. Inz-Fiz Zh 28(2), 340–345 (1975)

    MathSciNet  Google Scholar 

  7. Bieniasz, L.K.: Modeling electro-analytical experiments by the integral equation method. Springer, Berlin Heidelberg (2015)

    MATH  Google Scholar 

  8. Bojarski, B.: Taylor expansions and Sobolev spaces. Bull. Georg. Natl. Acad. Sci 5(2), (2011)

  9. Brezis, H.: Functional analysis. Sobolev spaces and partial differential equations, Springer Science Business Media (2010)

  10. Brunner, H.: Collocation methods for Volterra integral and related functional differential equations. Cambridge University Press, London (2004)

    Book  Google Scholar 

  11. Brunner, H.: The solution of Volterra integral equations of the first kind by piecewise polynomials. J. Inst. Math. Appl. 12, 295–302 (1973)

    Article  MathSciNet  Google Scholar 

  12. Canuto, C., Hussaini, M.Y., Quarteroni, A., Zang, T.A.: Spectral Methods on Fluid Dynamics. Springer-Verlag, New York (1988)

    Book  Google Scholar 

  13. Conte, D., Paternoster, B.: Multistep collocation methods for Volterra integral equations. J. Appl. Numer. Math. 59, 1721–1736 (2009)

    Article  MathSciNet  Google Scholar 

  14. Cavaliere, P., Cianchi, A.: Classical and approximate Taylor expansions of weakly differentiable functions. Ann. Acad. Sci. Fenn. Math. 39(2), 527–544 (2014)

    Article  MathSciNet  Google Scholar 

  15. Datta, KB., Mohan, BM.: Orthogonal functions in systems and control. World Sci Publishing Co (1995)

  16. Deimling, K.: Nonlinear Volterra integral equations of the first kind. Nonlinear Anal. 25, 951–957 (1995)

    Article  MathSciNet  Google Scholar 

  17. Ding, H.J., Wang, H.M., Chen, W.Q.: Analytical solution for the electrostatic dynamics of a non-homoge-neous spherically isotropic piezoelectric hollow sphere. Arch. Appl. Mech. 73, 49–62 (2003)

    Article  Google Scholar 

  18. Guru Sekar, RC., Murugesan, K.: STWS approach for Hammerstein system of non-linear Volterra integral equations of the second kind. J. Comput. Math. 1–14 (2016)

  19. Hackbusch, W.: Integral Equations: Theory and Numerical Treatment, second ed., vol. 68 of Guides to Applied Mathematics and Mechanics. B. G. Teubner, Stuttgart (1997)

  20. Hatamzadeh-Varmazyar, S., Masouri, Z., Babolian, E.: Numerical method for solving arbitrary linear differential equations using a set of orthogonal basis functions and operational matrix. J. Appl. Math. Model 40, 233–253 (2016)

    Article  MathSciNet  Google Scholar 

  21. Jiang, Z., Schoufelberger, W., Thoma, M., Wyner, A.: Block pulse functions and their applications in control systems. Springer-Verlag, New York (1992)

    Book  Google Scholar 

  22. Khan, N., Hashmi, M.S., Iqbal, S., Mahmood, T.: Optimal homotopy asymptotic method for solving Volterra integral equation of first kind. Alex. Eng. J. 53, 751–755 (2014)

    Article  Google Scholar 

  23. Ma, Y., Huang, J., Wang, C.: Sinc Nyström method for a class of nonlinear Volterra integral equations of the first kind. Adv. Differ. Equ. 1, 151 (2016)

    Article  Google Scholar 

  24. Maleknejad, K., Dehbozorgi, R.: Adaptive numerical approach based upon Chebyshev operational vector for nonlinear Volterra integral equations and its convergence analysis. J. Comput. Appl. Math. 344, 356–366 (2018)

    Article  MathSciNet  Google Scholar 

  25. Maleknejad, K., Saeedipoor, E.: Hybrid function method and convergence analysis for two-dimensional nonlinear integral equations. J. Comput. Appl. Math. 322, 96–108 (2017)

    Article  MathSciNet  Google Scholar 

  26. Maleknejad, K., Mollapourasl, R., Alizadeh, M.: Numerical solution of Volterra type integral equation of the first kind with wavelet basis. Appl. Math. Comput. 194(2), 400–405 (2007)

    MathSciNet  MATH  Google Scholar 

  27. Maleknejad, K., Rahimi, B.: Modification of block pulse functions and their application to solve numerically Volterra integral equation of the first kind. Commun. Nonlinear Sci. Numer. Simul. 16(6), 2469–2477 (2011)

    Article  MathSciNet  Google Scholar 

  28. Maleknejad, K., Hashemizadeh, E., Ezzati, R.: A new approach to the numerical solution of Volterra integral equations by using Bernstein’s approximation. Commun. Nonlinear Sci. Numer. Simul. 16(2), 647–655 (2011)

    Article  MathSciNet  Google Scholar 

  29. Masouri, Z., Babolian, E., Hatamzadeh-Varmazyar, S.: An expansion-iterative method for numerically solving Volterra integral equation of the first kind. Comput. Math. Appl. 59(4), 1491–1499 (2010)

    Article  MathSciNet  Google Scholar 

  30. Nedaiasl, K., Dehbozorgi, R., Maleknejad, K.: hp-version collocation method for a class of nonlinear Volterra integral equations of the first kind. Appl. Numer. Math. 150, 452–477 (2020)

    Article  MathSciNet  Google Scholar 

  31. Singh, I., Kumar, S.: Haar wavelet method for some nonlinear Volterra integral equations of the first kind. J. Comput. Appl. Math. 292, 541–552 (2016)

    Article  MathSciNet  Google Scholar 

  32. Tikhonov, A.N., Arsenin, V.Y.: Solutions of ill-posed problems. Winston, Washington DC (1977)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics, Iran University of Science and Technology, Narmak, Tehran, 16844, Iran

    Raziyeh Dehbozorgi & Khosrow Maleknejad

Authors
  1. Raziyeh Dehbozorgi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Khosrow Maleknejad
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Raziyeh Dehbozorgi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dehbozorgi, R., Maleknejad, K. Direct Operational Vector Scheme for First-Kind Nonlinear Volterra Integral Equations and Its Convergence Analysis. Mediterr. J. Math. 18, 31 (2021). https://doi.org/10.1007/s00009-020-01686-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00009-020-01686-1

Keywords

Mathematics Subject Classification

Search

Navigation