Abstract
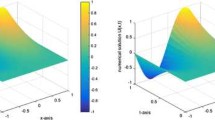
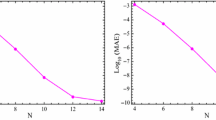
In this paper, we introduce a numerical method for solving time-fractional order telegraph equation. The method depends basically on an expansion of approximated solution in a series of Sinc function and shifted Legendre polynomials. The fractional derivative is expressed in the Caputo definition of fractional derivatives. The expansion coefficients are then determined by reducing the time-fractional order telegraph equation with its boundary and initial conditions to a system of algebraic equations for these coefficients. This system can be solved numerically using the Newton’s iteration method. Several numerical examples are introduced to demonstrate the reliability and effectiveness of the introduced method.
Similar content being viewed by others
References
Babolian E., Eftekhari A., Saadatmandi A.: A Sinc-Galerkin technique for the numerical solution of a class of singular boundary value problems. Comput. Appl. Math. 34, 45–63 (2015)
Bhrawy, A.H., Al-Shomrani, M.M.: A shifted Legendre spectral method for fractional-order multi-point boundary value problems. Adv. Differ. Equ. 2012 (2012) (article 8)
Biazar J., Ebrahimi H., Ayati Z.: An approximation to the solution of telegraph equation by variational iteration method. Numer. Methods Partial Differ. Equ. 25(4), 779–801 (2009)
Cascaval R.C., Eckstein E.C., Frota L., Goldstein J.A.: Fractional telegraph equations. J. Math. Anal. Appl. 276, 145–159 (2002)
Chen J., Liu F., Anh V.: Analytical solution for the time-fractional telegraph equation by the method of separating variables. J. Math. Anal. Appl. 338(2), 1364–1377 (2008)
Dalir M., Bashour M.: Applications of fractional calculus. Appl. Math. Sci. 4, 1021–1032 (2010)
Debnath L.: Nonlinear Partial Differential Equations for Scientists and Engineers. Birkhäuser, Boston (1997)
Dehghan M., Lakestani M.: The use of Chebyshev cardinal functions for solution of the second-order one-dimensional telegraph equation. Numer. Methods Partial Differ. Equ. 25, 931–7938 (2009)
Das S., Vishal K., Gupta P.K., Yildirim A.: An approximate analytical solution of time-fractional telegraph equation. Appl. Math. Comput. 217(18), 7405–7411 (2011)
Del-Castillo-Negrete D., Carreras B.A., Lynch V.E.: Front dynamics in reaction–diffusion systems with LTvy flights: a fractional diffusion approach. Phys. Rev. Lett. 91(1), 18301–18304 (2003)
Garg M., Sharmah A.: Solution of space-time fractional telegraph equation by adomian decomposition method. J. Inequal. Special Funct. 2(1), 1–7 (2011)
Gorenflo R., Mainardi F., Moretti D., Pagnini G., Paradisi P.: Discrete random walk models for space-time fractional diffusion. Chem. Phys. 284, 521–541 (2002)
Hayat U., Mohyud-Din S.T.: Homotopy perturbation technique for time-fractional telegraph equations. Int. J. Mod. Theor. Phys. 2(1), 33–41 (2013)
Heydari M.H., Hooshmandasl M.R., Mohammadi F.: Two-dimensional Legendre wavelets for solving time-fractional telegraph equation. Adv. Appl. Math. Mech. 6(2), 247–260 (2014)
Hosseini V.R., Chen W., Avazzadeh Z.: Numerical solution of fractional telegraph equation by using radial basis functions. Eng. Anal. Bound. Elem. 38, 31–39 (2014)
Kaya D.: A new approach to the telegraph equation: An application of the decomposition method. Bull. Inst. Math. Acad. Sin. 28(1), 51–57 (2000)
Kilbas A.A., Srivastava H.M., Trujillo J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, San Diego (2006)
Lund J., Bowers K.L.: Sinc Methods for Quadrature and Differential Equations. SIAM, Philadelphia (1992)
Mainardi F., Paradisi P.: Fractional diffusive waves. J. Comput. Acoust. 9(4), 1417–1436 (2001)
Mao, Z., Xiao, A., Yu, Z., Shi, L.: Sinc-Chebyshev collocation method for a class of fractional diffusion-wave equations. Sci. World J. 2014 (article ID 143983)(2014)
Miller K. S., Ross B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)
Nagy A.M., Sweilam N.H.: An efficient method for solving fractional HodgkinHuxley model. Phys. Lett. A. 378, 1980–1984 (2014)
Podlubny I.: Fractional Differential Equations. Academic Press, New York (1999)
Roussy G., Pearcy J.A.: Foundations and Industrial Applications of Microwaves and Radio Frequency Fields. Wiley, New York (1995)
Saadatmandi A., Dehghan M., Azizi M.R.: The Sinc-Legendre collocation method for a class of fractional convection–diffusion equations with variable coefficients. Commun. Nonlinear Sci. Numer. Simul. 17(11), 4125–4136 (2012)
Sokolov I.M., Klafter J., Blumen A.: Ballistic versus diffusive pair-dispersion in the Richardson regime. Phys. Rev. E. 61(3), 2717–2722 (2000)
Stenger, F.: Handbook of Sinc Numerical Methods. Chapman & Hall/CRC Numerical Analysis and Scientific Computing, CRC Press, Boca Raton (2011)
Sweilam N.H., Nagy A.M.: Numerical solution of fractional wave equation using Crank–Nicholson method. World Appl. Sci. J. (WASJ) 13, 71–75 (2011)
Sweilam N.H., Nagy A.M., El-Sayed A.A.: Second kind shifted Chebyshev polynomials for solving space fractional order diffusion equation. Chaos Solitons Fractals 73, 141–147 (2015)
Sweilam N.H., Nagy A.M., El-Sayed A.A.: On the numerical solution of space fractional order diffusion equation via shifted Chebyshev polynomials of the third kind. J. King Saud Univ. Sci. 28(1), 41–47 (2016)
Szabo T.L., Wu J.: A model for longitudinal and shear wave propagation in viscoelastic media. J. Acoust. Soc. Am. 107(5), 2437–2446 (2000)
Yildirim A.: He’s homotopy perturbation method for solving the space- and time-fractional telegraph equations. Int. J. Comput. Math. 87, 2998–3006 (2010)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sweilam, N.H., Nagy, A.M. & El-Sayed, A.A. Solving Time-Fractional Order Telegraph Equation Via Sinc–Legendre Collocation Method. Mediterr. J. Math. 13, 5119–5133 (2016). https://doi.org/10.1007/s00009-016-0796-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00009-016-0796-3