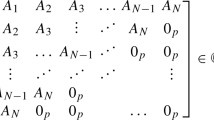Skip to main content
SpringerLink
Log in

An Extension of the Geronimus Transformation for Orthogonal Matrix Polynomials on the Real Line

  • Published:
Mediterranean Journal of Mathematics Aims and scope Submit manuscript

Abstract

We consider matrix polynomials orthogonal with respect to a sesquilinear form \({\langle{\cdot,\cdot}\rangle_W}\), such that

$$ \langle{P(t)W(t),Q(t)W(t)}_{W}\rangle=\int_{\mathfrak{I}}P(t){\rm d} \mu Q(t)^{T}, \quad P,Q \in \mathbb{P}^{p\times p}[t], $$

where \({\mu}\) is a symmetric, positive definite matrix of measures supported in some infinite subset \({\mathfrak{I}}\) of the real line, and W(t) is a matrix polynomial of degree N. We deduce the integral representation of such sesquilinear forms in such a way that a Sobolev-type inner product appears. We obtain a connection formula between the sequences of matrix polynomials orthogonal with respect to \({\mu}\) and \({\langle{\cdot,\cdot}\rangle_W}\), as well as a relation between the corresponding block Jacobi and Hessenberg type matrices.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Akhiezer, N.I.: Classical Moment Problem and Related Questions in Analysis. Oliver & Boyd, Edinburgh (1965)

  2. Álvarez-Fernández, C., Ariznabarreta, G., García-Ardila, J. C., Mañas, M., Marcellán, F.: Christoffel transformations for matrix orthogonal polynomials in the real line and the non-Abelian 2D Toda lattice hierarchy. Int. Math. Res. Not. (2016). doi:10.1093/imrn/rnw027

  3. Álvarez-Fernández, C., Ariznabarreta, G., García-Ardila, J. C., Mañas, M., Marcellán, F.: Transformation theory and Christoffel formulas for matrix biorthogonal polynomials on the real line. arXiv:1605.04617 [math.CA]

  4. Andrews, G. E., Askey, R., Roy, R.: Special Functions. Cambridge Univ. Press, Cambridge (1999)

  5. Aptekarev, A.I., Nikishin, E.M.: The scattering problem for a discrete Sturm– Liouville operator. Math. USSR Sb. 49, 325355 (1984)

  6. Ariznabarreta, G., Mañas, M.: Darboux transformations for multivariate orthogonal polynomials. arXiv preprint: arXiv:1503.04786

  7. Cantero M.J., Marcellán F., Moral L., Velázquez L.: Darboux transformations for CMV matrices. Adv. Math. 208, 122–206 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  8. Castro M.M., Grünbaum F.A.: Orthogonal matrix polynomials satisfying first order differential equations: a collection of instructive examples. J. Nonlinear Math. Phys. 12(2), 63–76 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  9. Chihara, T. S.: An Introduction to Orthogonal Polynomials. In : Mathematics and its Applications Series, vol. 13. Gordon and Breach Science Publishers, New York-London-Paris (1978)

  10. Cooke, R.G.: Infinite Matrices and Sequence Spaces. Macmillan & Co., Ltd., London (1950)

  11. Choque Rivero A.E., Garza L.E.: Moment perturbation of matrix polynomials. Integral Transform. Spec. Funct. 26, 177–191 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  12. Damanik D., Pushnitski A., Simon B.: The analytic theory of matrix orthogonal polynomials. Surv. Approx. Theory 4, 1–85 (2008)

    MathSciNet  MATH  Google Scholar 

  13. Derevyagin M., García-Ardila J.C., Marcellán F.: Multiple Geronimus transformations. Linear Algebra Appl 454, 158–183 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  14. Derevyagin M., Marcellán F.: A note on the Geronimus transformation and Sobolev orthogonal polynomials. Numer. Algorithms 67, 271–287 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  15. Durán A.J.: Markov’s theorem for orthogonal matrix polynomials. J. Math. 48, 1180–1195 (1996)

    MathSciNet  MATH  Google Scholar 

  16. Durán A.J.: Ratio asymptotic for orthogonal matrix polynomials. J. Approx. Theory 100, 304–344 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  17. Durán A.J., Grünbaum F.A.: Orthogonal matrix polynomials, scalar-type Rodrigues’ formulas and Pearson equations. J. Approx. Theory 134, 267–280 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  18. Durán A.J., Grünbaum FA: A survey on orthogonal matrix polynomials satisfying second order differential equations. J. Comput. Appl. Math. 178, 169–190 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  19. Durán, A.J., López-Rodríguez, P.: Orthogonal matrix polynomials: Zeros and Blumenthal’s theorem. J. Approx. Theory 84, 96–118 (1996)

  20. Durán A.J., Van Assche W.: Orthogonal matrix polynomials and higher-order recurrence relations. Linear Algebra Appl. 219, 261–280 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  21. Gelfand I., Gelfand S., Retakh V., Wilson RL: Quasideterminants. Adv. Math. 193, 56–141 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  22. Gohberg, I., Lancaster, P., Rodman, L.: Matrix Polynomials. Computer Science and Applied Mathematics. Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York-London (1982)

  23. Grünbaum, F.A.: The Darboux process and a noncommutative bispectral problem: some explorations and challenges. In: Geometric aspects of analysis and mechanics, vol. 292, Progr. Math, pp. 161–177. BirkhSuser/Springer, New York (2011)

  24. Grünbaum F.A., Haine L.: Bispectral Darboux transformations: an extension of the Krall polynomials. Int. Math. Res. Not. 8, 359–392 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  25. Grünbaum F.A., Yakimov M.: Discrete bispectral Darboux transformations from Jacobi operators. Pac. J. Math. 204, 395–431 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  26. Horn, R.A., Johnson, C.R.: Matrix Analysis, Second edn. Cambridge University Press, Cambridge (2013)

  27. Lang, S.: Algebra, Third edn. Springer-Verlag, New York (2005)

  28. Markus, A.S.: Introduction to the spectral theory of polynomials operator pencil. Translated from the Russian by H. H. McFaden. Translation edited by Ben Silver. With an appendix by M. V. Keldysh. Translations of Mathematical Monographs, vol. 71. Am. Math. Soc., Providence, RI (1988)

  29. Miranian L.: Matrix valued orthogonal polynomials on the real line: some extensions of the classical theory. J. Phys. A 38, 5731–5749 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  30. Rowen, L.: Ring Theory, vol. I. Academic Press, San Diego (1988)

  31. Sinap A., Van Assche W.: Polynomial interpolation and Gaussian quadrature for matrix-valued functions. Linear Algebra Appl. 207, 71–114 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  32. Sinap A., Van Assche W.: Orthogonal matrix polynomials and applications. J. Comput. Appl. Math. 66, 27–52 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  33. Zhedanov, A.: Rational spectral transformations and orthogonal polynomials. J. Comput. Appl. Math. 85, 67–86 (1997)

Download references

Author information

Authors and Affiliations

  1. Departamento de Matemáticas, Universidad Carlos III de Madrid, Avenida Universidad 30, Leganés, Spain

    Juan Carlos García-Ardila & Francisco Marcellán

  2. Facultad de Ciencias, Universidad de Colima, Bernal Díaz del Castillo 340, Colima, Mexico

    Luis E. Garza

  3. Instituto de Ciencias Matemáticas (ICMAT), C/ Nicolás Cabrera, 13-15, Campus de Cantoblanco UAM, 28049, Madrid, Spain

    Francisco Marcellán

Authors
  1. Juan Carlos García-Ardila
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Luis E. Garza
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Francisco Marcellán
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Luis E. Garza.

Additional information

The work of Luis E. Garza was supported by Conacyt (México), Grant 156668. The work of Juan Carlos García-Ardila and Francisco Marcellán has been supported by Dirección General de Investigación, Científica y Técnica , Ministerio de Economía y Competitividad of Spain, Grant MTM2015-65888-C4-2-P.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

García-Ardila, J.C., Garza, L.E. & Marcellán, F. An Extension of the Geronimus Transformation for Orthogonal Matrix Polynomials on the Real Line. Mediterr. J. Math. 13, 5009–5032 (2016). https://doi.org/10.1007/s00009-016-0789-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00009-016-0789-2

Mathematics Subject Classification

Keywords

Search

Navigation