Skip to main content
SpringerLink
Log in

Fractional Calculus on Fractal Interpolation for a Sequence of Data with Countable Iterated Function System

  • Published:
Mediterranean Journal of Mathematics Aims and scope Submit manuscript

Abstract

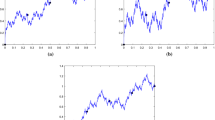
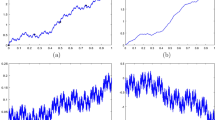
In recent years, the concept of fractal analysis is the best nonlinear tool towards understanding the complexities in nature. Especially, fractal interpolation has flexibility for approximation of nonlinear data obtained from the engineering and scientific experiments. Random fractals and attractors of some iterated function systems are more appropriate examples of the continuous everywhere and nowhere differentiable (highly irregular) functions, hence fractional calculus is a mathematical operator which best suits for analyzing such a function. The present study deals the existence of fractal interpolation function (FIF) for a sequence of data \({\{(x_n,y_n):n\geq 2\}}\) with countable iterated function system, where \({x_n}\) is a monotone and bounded sequence, \({y_n}\) is a bounded sequence. The integer order integral of FIF for sequence of data is revealed if the value of the integral is known at the initial endpoint or final endpoint. Besides, Riemann–Liouville fractional calculus of fractal interpolation function had been investigated with numerical examples for analyzing the results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Mandelbrot B.B.: The Fractal Geometry of Nature. W.H. Freeman and Company, New York (1983)

    MATH  Google Scholar 

  2. Hutchinson J.E.: Fractals and self-similarity. Indiana Univ. Math. J. 30, 313–747 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  3. Barnsley M.F.: Fractals Everywhere. 2nd edn. Academic Press, USA (1993)

    MATH  Google Scholar 

  4. Barnsley M.F.: Fractal functions and interpolation. Constr. Approx. 2, 303–329 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  5. Barnsley M.F., Harrington A.N.: The calculus of fractal interpolation functions. J. Approx. Theory 57, 14–34 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  6. Viswanathan P., Chand A.K.B., Navascues M.A.: Fractal perturbation preserving fundamental shapes: bounds on the scale factors. J. Math. Anal. Appl. 419, 804–817 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chand A.K.B., Kapoor G.P.: Hidden variable bivariate fractal interpolation surfaces. Fractals 11(3), 277–288 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  8. Secelean N.A.: The fractal interpolation for countable systems of data, Beograd University, Publikacije. Electrotehn. Fak. ser. Matematika 14, 11–19 (2003)

    MathSciNet  MATH  Google Scholar 

  9. Secelean N.A.: The existence of the attractor of countable iterated function systems. Mediterr. J. Math. 9, 61–79 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  10. Uthayakumar R., Gowrisankar A.: Fractals in product fuzzy metric space, fractals, wavelets, and their applications. Springer Proc. Math. Stat. 92, 157–164 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  11. Uthayakumar R., Gowrisankar A.: Generation of fractals via self-similar group of Kannan iterated function system. Appl. Math. Inf. Sci. 9(6), 3245–3250 (2015)

    MathSciNet  Google Scholar 

  12. Massopust, P.R.: Fractal functions. In: Fractal Surfaces and Wavelets. Academic Press, Orlando (1994)

  13. Amo E.D., Carrillo M.D., Sanchez J.F.: PCF self-similar sets and fractal interpolation. Math. Comput. Simul. 92, 28–39 (2013)

    Article  MathSciNet  Google Scholar 

  14. Navascues N.A.: Fractal approximation. Complex Anal. Oper. Theory 4, 953–974 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  15. Miller K.S., Ross B.: An introduction to the fractional calculus and fractional differential equations. Wiley, New York (1993)

    MATH  Google Scholar 

  16. Ross B.: Fractional Calculus and its Applications, Berlin. Springer, Heidelberg (1975)

    Book  Google Scholar 

  17. Tatom F.B.: The relationship between fractional calculus and fractal. Fractals 3(1), 217–229 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  18. Liang Y.S., Su W.Y.: The relationship between the fractal dimensions of a type of fractal functions and the order of their fractional calculus. Chaos Solitons Fractals 34, 682–692 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  19. Ruan H.-J., Su W.-Y., Yao K.: Box dimension and fractional integral of linear fractal interpolation functions. J. Approx. Theory 161, 187–197 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  20. Secelean N.A.: Approximation of the attractor of a countable iterated function system. Gen. Math. 17(3), 221–231 (2009)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, The Gandhigram Rural Institute, Deemed University, Gandhigram, Dindigul, Tamil Nadu, 624 302, India

    A. Gowrisankar & R. Uthayakumar

Authors
  1. A. Gowrisankar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Uthayakumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Gowrisankar.

Additional information

The research work has been supported by University Grants Commission, Government of India, New Delhi, India, under the scheme of UGC-MRP with Grant No.: F.No. 42-21/2013 (SR)/dated 12.03.2013.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gowrisankar, A., Uthayakumar, R. Fractional Calculus on Fractal Interpolation for a Sequence of Data with Countable Iterated Function System. Mediterr. J. Math. 13, 3887–3906 (2016). https://doi.org/10.1007/s00009-016-0720-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00009-016-0720-x

Mathematics Subject Classification

Keywords

Search

Navigation