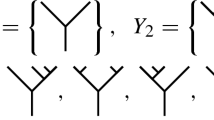Skip to main content
SpringerLink
Log in

Posetted Trees and Baker-Campbell-Hausdorff Product

  • Published:
Mediterranean Journal of Mathematics Aims and scope Submit manuscript

Abstract

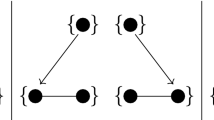
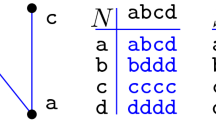
In this paper, we use some typical tools of algebraic operads and homotopy transfer theory, in order to give a simple and elementary combinatorial description of the Baker-Campbell-Hausdorff formula. More precisely, we exploit the usual operadic notion of planar rooted trees, enriched with the notion of subroots, and we define a posetted tree as a planar rooted tree endowed with a monotone labelling of leaves, with elements in a partially ordered set. The main result of this paper is an explicit expression of the Baker-Campbell-Hausdorff product as a sum of iterated brackets over an indexing set of posetted binary trees.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. H. Baker, Alternants and continuous groups, Proc. London Math. Soc. 3 (1905), no. 2, 24-47.

  2. E. Burgunder, Eulerian idempotent and Kashiwara-Vergne conjecture, Ann. Inst. Fourier (Grenoble) 58 (2008), no. 4, 1153-1184.

  3. J. Campbell, On a law of combination of operators, Proc. London Math. Soc. 28 (1897), no. 1, 381-390; 29 (1898), 14-32.

  4. F. Casas and A. Murua, An efficient algorithm for computing the Baker-Campbell-Hausdorff series and some of its applications series, J. Math. Phys. 50 (2009), 033513, 23pp.

    Google Scholar 

  5. J. J. Duistermaat and J. A. C. Kolk, Lie Groups, Springer Universitext (2000).

  6. E. Dynkin, Calculation of the coefficients of the Campbell-Hausdorff formula, Dokl. Akad. Nauk. 57 (1947), 323-326. An English translation may be found in: E. B. Dynkin, A. A. Yushkevich, G. M. Seitz, A. L. Onishchik (Eds.), Selected Papers of E. B. Dynkin with Commentary, American Mathematical Society/International Press, Providence, R.I./Cambridge, Mass., (2000).

  7. Fiorenza D., Manetti M.: L ∞-structures on mapping cones, Algebra & Number Theory 1, 301–330 (2007) arXiv:math/0601312

    Article  MathSciNet  MATH  Google Scholar 

  8. Fiorenza D., Manetti M., Martinengo E.: Cosimplicial DGLAs in deformation theory, Communications in Algebra 40, 2243–2260 (2012) arXiv:0803.0399v1

    Article  MathSciNet  MATH  Google Scholar 

  9. B. C. Hall, Lie Groups, Lie Algebras, and representations. An elementary introduction, Graduate Texts in Mathematics 222, Springer-Verlag, New York Berlin, (2003).

  10. Hausdorff F.: Die symbolische Exponentialformel in der Gruppentheorie, Ber. Verh. Saechs. Akad. Wiss., Leipzig, Math. Phys. Kl. 58, 19–48 (1906)

    Google Scholar 

  11. Kathotia V.: Kontsevich universal formula for quantization and the Campbell-Baker-Hausdorff formula, Internat. J. Math. 11, 523–551 (2000) arXiv:math/9811174v2

    MathSciNet  MATH  Google Scholar 

  12. Kontsevich M.: Deformation quantization of Poisson manifolds, I, Letters in Mathematical Physics 66, 157–216 (2003) arXiv:q-alg/9709040

    Article  MathSciNet  MATH  Google Scholar 

  13. J-L. Loday, Série de Hausdorff, idempotents eulériens et algèbres de Hopf, Exposition. Math. 12 (1994), no. 2, 165-178.

  14. J.-L. Loday and B. Vallette, Algebraic Operads, Grundlehren der mathematischen Wissenschaften 346, Springer-Verlag (2012).

  15. Manetti M.: A relative version of the ordinary perturbation lemma, Rend. Mat. Appl. 30(7), 221–238 (2010) arXiv:1002.0683

    MathSciNet  MATH  Google Scholar 

  16. M. Markl, S. Shnider and J. Stasheff, Operads in algebra, topology and physics, Mathematical Surveys and Monographs 96, American Mathematical Society, Providence, RI, (2002).

  17. Mielnik B., Plebańsky J.: Combinatorial approach to Baker-Campbell-Hausdorff exponents, Ann. Inst. H. Poincaré Sect. A (N.S.) 12, 215–254 (1970)

    MATH  Google Scholar 

  18. A. Murua, The Hopf algebra of rooted trees, free Lie algebras, and Lie series, Found. Comp. Math. 6 (2006), no. 4, 387-426.

  19. O. Ore, Theory of graphs, Colloquium publications 38, American Mathematical Society, Providence, RI, (1962).

  20. Oteo J.: The Baker-Campbell-Hausdorff formula and nested commutator identities, J. Math. Phys. 32, 419–424 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  21. Ranjan D., Pontelli E., Gupta G.: Data structures for order-sensitive predicates in parallel nondeterministic system, Acta Informatica 37, 21–43 (2000)

    Article  MATH  Google Scholar 

  22. Reinsch M.W.: A simple expression for the terms in the Baker-Campbell-Hausdorff series J. Math. Phys. 41, 2434–2442 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  23. C. Reutenauer, Theorem of Poincaré-Birkhoff-Witt, logarithm and symmetric group representations of degrees equal to Stirling numbers, Combinatoire énumérative (Montreal, Que., 1985 Quebec, Que., 1985), 267-284, Lecture Notes in Math. 1234, Springer, Berlin, 1986.

  24. Torossian C.: Sur la formule combinatoire de Kashiwara-Vergne, J. Lie Theory 12, 597–616 (2002)

    MathSciNet  MATH  Google Scholar 

  25. Weyrauch M., Scholz D.: Computing the Baker-Campbell-Hausdorff series and the Zassenhaus product, Computer Physics Communications 180, 1558–1565 (2009)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Matematica, Università degli Studi di Bari, Via E. Orabona 4, I-70125, Bari, Italy

    Donatella Iacono

  2. Dipartimento di Matematica “Guido Castelnuovo”, Università degli Studi di Roma La Sapienza, P.le Aldo Moro 5, I-00185, Roma, Italy

    Marco Manetti

Authors
  1. Donatella Iacono
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marco Manetti
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Donatella Iacono.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Iacono, D., Manetti, M. Posetted Trees and Baker-Campbell-Hausdorff Product. Mediterr. J. Math. 10, 611–623 (2013). https://doi.org/10.1007/s00009-012-0235-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00009-012-0235-z

2010 Mathematics Subject Classification

Keywords

Search

Navigation