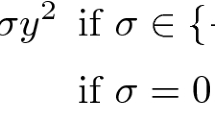Produit d’inversions elliptiques ou hyperboliques

Abstract.

Let x and y be orthogonal coordinates of a point M (u = ax + iby or ax + ɛ by) of a plane where as x′ and y′ are orthogonal coordinates of a point M′(V = ax′ + iby′ or ax′ + ɛ by′) inverse of M in the elliptic hyperbolic inversion $u\bar v = k{\text{ or }}(u - \alpha )(\bar v - \alpha ) = k'$ (k and k′ positive) $\bar v$ designating the conjugate of v while i and ɛ are Clifford numbers such that i ² = −1 and ɛ² = 1 (a and b are real). O is the origin of axises. Ox is the axis of inversions. We study particularly the product of two inversions.