Introduction

Dom Paul Bellot (1876–1944) was an influential French Benedictine monk and architect in the first half of the twentieth century. He made strong and powerful religious architecture arguing that architecture should be both useful and beautiful. Rejecting the modernist view of form following function, Dom Bellot’s philosophy was that if something was functional, it must also surpass our every day expectations and delight the senses and the mind.

Le beau consiste dans une juste proportion des choses, c’ est-à-dire une disposition, un ordre interne qui est pour l’ esprit, qui contemple derrière les impressions sensibles, harmonie et clarité. (Bellot 1948, p. 101; Willis 1994).

According to Dom Bellot, true beauty lies in the right proportion of things, an internal order of the spirit, which acts on our senses, with harmony and clarity [translation by the author].

Dom Bellot also wrote: “L’apprentissage de la vie monastique, fort heureusement, me permit de me livrer vraiment à la réflexion, de me dégager de la fascination des forms anciennes et de découvrir, pour mon profit, l’âme même de la tradition, son courant vital, et, en lui, les principes perdurables de l’art et du gout”. [The monastic life, fortunately, enabled me to reflect on and to clear my fascination for ancient forms and discover, for my benefit, the soul of tradition, its vital power, and in it, the sustaining principles of art and style (translation by the author)] (Bellot 1948, p. 43; Willis 1994).

This paper considers the question: which generating principle of architectural proportion did Dom Bellot exactly found? Did he—as Golden Section believer—really build up his geometrical schemes according to this irrational ratio 1.618034(φ)? This paper wants to prove that his discoveries of the Golden Section are actually based on the rational ratios 5:3 (1.666…), 4:3 (1.333…) and 1:2.

An additional component of this review is the geometrical study of the chapel of the former Augustinian College in Eindhoven. This study was carried out from the perspective of an architect-designer. This study is based on the conditions indicated in the paper Under Siege: The Golden Mean in Architecture by M. J. Ostwald. This paper says that proportional analysis should only be undertaken where there is clear, visible evidence that the architect was aware of the Golden Mean (Ostwald 2002). This study would also refers to the paper Contra Divinam Proportionem. (Frascari et al. 1998) which says that during antiquity ratios were used to manifest incommensurable entities. These approximations were judged perfectly acceptable.

Biography

The life of Dom Bellot is described in detail in the introduction of the book Propos d’un Bâtisseur du bon Dieu (Bellot 1948, 13–25), and in Dom Bellot Moine-Architecte 1876–1944 (Culot et al. 1996, pp. 29–79) (Fig. 1).

Fig. 1
figure 1

Dom Paul Bellot. In August 1928, Bellot left Oosterhout and continued his practice at l’Abbey Saint-Paul de Wisques, in France. He also worked on the launch of “l’Arche”, a group of French artists and architects (also the Perret brothers) who came together in 1919 to make a Christian art reform in France. [Guéné 2000; Pouls 2002]

Full size image

Paul Bellot was the eldest son of an architect-surveyor, who was an admirer of the French architect and theorist, Viollet-le-Duc (1959). From 1894 to 1900 he studied architecture at the Ecole des Beaux-Arts, in Paris. In 1902 he joined the Benedictine community in Solesmes. He had to live according to the rules of St. Benedict (ca. 480–547). This community was forced to leave France by the anti-clerical laws of 1901. Dom Paul Bellot built new abbeys in England (Quarr Abbey) and in the Netherlands (St-Paulus Abby Oosterhout). From 1921 to 1928 he had his own architectural practice in Oosterhout. He designed monastic buildings in France, the Netherlands and Belgium. In September 1927, Hans Van der Laan, a young Dutch architect, entered this Benedictine community. His introduction to Dom Bellot can be traced as the catalyst that led him to the discovery of the plastic number (Van der Laan 1949, 1960; Remery 2010, pp. 53–54). In August 1928, Bellot left Oosterhout and continued his practice at l’Abbey Saint-Paul de Wisques, in France. He also worked on the launch of “l’Arche”, a group of French artists and architects (including the Perret brothers) who came together in 1919 to make a Christian art reform in France. (Guéné 2000; Pouls 2002). In 1934 Dom Bellot travelled to Canada to give a series of architecture lectures. He was trapped in Canada by the outbreak of the Second World War. He continued working there until his death.

Method

Literature Review

Considering the literature that deals with the work and the proportional system of Dom Bellot, two features can be identified. On the one hand, in most of the literature about Dom Bellot, there are no details given about his proportionality. If anything is mentioned, it is mostly about the Golden Section.

On the other hand, the information provided by Dom Bellot is extensive and diverse. He expressed his thoughts in publications, through lectures and via correspondence. Despite this, it is remarkable that he kept his proportional system quite secret and out of the public eye. This paper is one of the few examples where his proportional system is investigated.

Dom Bellot published the book Une Oeuvre d’Architecture Moderne in the autumn of 1927 (Bellot 1927; Culot et al. 1996, p. 54) (Fig. 2). This book presents the first seven buildings of his practice in Oosterhout. His first realised works are: Sint-Paulus Abdij at Oosterhout; Quarr Abbey on the Isle of Wight (UK); the church, rectory and school at Noordhoek; the sisters’ kindergarten and convent at Bavel; the Augustinian college and chapel at Eindhoven; the church at Heerlen; and the cemetery chapel at Bloemendaal. In the introduction to this book written by Henri Charlier, the Pythagorean triangle is said to be a basic form used by Dom Bellot. This is a numerical and geometrical system, and not an approximate and irrational Golden Mean system. Henri Charlier wrote:

Fig. 2
figure 2

Cover of Une Oeuvre d’Architecture Moderne by Dom Bellot

Full size image

Toutes les grandes architectures du passé ont usé de systèmes semblables. Les Egyptiens avaient réuni les principales proportions dont ils usaient en un triangle rectangle dont les côtés étaient égaux à 3,4,5. …Dom Bellot a ainsi en tête certaines proportions qui ont pour origine un rapport du triangle égyptien, mais beaucoup plus riche de proportions heureuses. Nous ne nous étendrons point là-dessus, le monde modern galvaudant tout ce qu’on lui livre (Bellot 1927, p. 12).

All great architectures of the past have used similar systems. The Egyptians got their main proportions out of the triangle with sides equal to 3,4,5. …

Dom Bellot also has in mind some proportions that are caused by a report of the Egyptian triangle, but much more rich of happy proportions. We keep quiet about this, the modern world abused all the things that you deliver her (Bellot 1927).

After Dom Bellot’s death, the book Propos d’un Bâtisseur du bon Dieu was published (Bellot 1948) (Fig. 3). The book is a collection of the lectures given by Dom Bellot in Canada, in 1934. The general theme of his lectures was innovation according to true tradition (innover selon la juste tradition, Bellot 1948). He divides his lectures into aesthetic and technical questions:

Fig. 3
figure 3

Cover of Propos d’un Bâtisseur du bon Dieu by Dom Bellot

Full size image

  • Aesthetic questions: The revival of art and good taste; the conditions for a true style; the conditions for timeless beauty; the ideal and the asceticism of Christian art; Formalism and rationalist architecture in their relationship with beauty.

  • Technical questions: Primacy of form on light and colour; proportion; overview: genesis of forms; colour.

In his lecture on proportions Dom Bellot explains that the Benedictines gave him the book Zur Ästhetik der Beuroner Schule (Lenz 1865; Erens 1910). This thin book was written by Dom Desiderius Lenz, a member of the Benedictine Abbey of Beuron in Germany. Lenz believed that real art is equal to order, as an abstraction of nature. In 1910, he also received a book at Quarr Abbey in England, written by Dom Odilo Wolff, an Austrian Benedictine (Wolff 1887). In Wolff’s view, the hexagon made of two equilateral triangles of 60° (the star of David) governed the art of the ancient world (Fig. 4). Dom Bellot built the church of Quarr Abbey upon this principle from Wolff (Bellot 1948, p. 109). Dom Bellot slightly adapted the hexagram by Wolff and came to his mysterious set-square (Fig. 7), as an initiator of all types of harmonies (Bellot 1948, pp. 110–111).

Fig. 4
figure 4

According to Wolff, figure in the book Bouwkundige Compositie by architect Jan Stuyt (1933)

Full size image

A third source of information is Le Centre des Archives Nationales du Monde du Travail (CAMT) in Roubaix. There the private archive of Dom Bellot can be found, donated by the Benedictines from l’Abbeye Saint Paul de Wisques in 2003. The archive is a treasure-trove of information about the life and the work of Dom Bellot (Hottin 2003) which has never been investigated. Also stored in the CAMT are studies about St Thomas Aquinas, relating to beauty. Dom Bellot writes: “St Thomas Aquinas embodies the doctrines of Plato, Aristotle and Augustine, that tell us that order is essential to beauty” (Bellot 1948, p. 61, note 5). In the archive one can find Dom Bellot’s studies in 1918 of The Dictionnaire and Entretiens, written by Viollet-le-Duc (1854, 1860), and Histoire de l’Architecture by Choisy (1899), a French art historian and engineer. The latter helped him to put the ideas of Viollet-le-Duc into practice (Culot et al. 1996).

Fourth on the list of information sources is the journal L’Arche. Dom Bellot was on its administrative review committee (Simmins 1997). Books about this renewal in art are Nouvelles Théories by Maurice Denis (1922), and Art et Scolastique by Jacques Maritain (1920). Finally the last source of information given by Dom Bellot is the personal correspondence between him and Dom Côté in Canada (Bellot 1933–1937), along with the correspondence with the young Canadian architects Dufresne and Courchesne, in the CAMT. Dom Bellot also wrote an article about the works of his Dutch collaborator and architect Van de Leur (Bellot 1935).

The second part of this literature review covers studies dealing with the body of work of Dom Bellot. In France, a good reference book is Dom Bellot, Moine-Architecte (Culot et al. 1996). In Canada, Tardif-Painchaud (1978) published Dom Bellot et l’Architecture Religious au Quebec. In the Netherlands, Ard Lukassen and Anton Lukassen (2014) created a website about Dom Bellot. However, in all of these publications, there are no details given about the proportionality in his work. One can also find a number of publications about the buildings created by Dom Bellot including Quarr Abbey (Abbott 2004) and the majestic Abbey Saint-Benoît-du-Lac in Canada (Langlois 2008; Bergeron et al. 1997).

It was no easy task to locate publications that consider proportionality in his architecture. One example is the thesis by Willis (1994) which comments on the lectures given by Dom Bellot. Next, Simmins (1997) published his study Dom Bellot: Towards a Theory of Architecture were he observed that a triangulated crossing system based on the Golden Section can be gleaned from the drawings of Dom Bellot. Simmins also observed that from these starting points, a number of specific ratios could be developed, not limited to the Golden Section, but also including root rectangles and their fractional equivalents. Simmins also mentioned the relationship to the term dynamic symmetry developed by the American Hambridge (Hambridge 1920), and that similar sentiments are expressed in the works of French scholars of the period (Ghyka 1931). And third, an article about Joseph Philippe, Bellot’s main collaborator in France, was published by Wintrebert (2007). According to this article, Philippe was inspired by the works of Ghyka (1931). Dom Bellot taught his disciple his method and this was the reason that Philippe used Bellot’s unusual 58° 17′ and 31°43′ angled triangle (Fig. 7). From Lukassen and Lukassen (2014) it is possible to discover that Henk Charles Van de Leur, Bellot main collaborator in The Netherlands also used this unusual set square. The present paper is virtually the first and only publication that shows that Dom Bellot actually used a triangulated crossing system based on the Golden Ratio.

Research on Site

Measurements and geometrical studies of the chapel in Eindhoven were made in situ. In the spring of 2012, the author worked as an architect on an exhibition in this chapel. The atmosphere of the chapel and the movement of going up the stairs to the chapel had a sensitising effect on the research. Out of this fascination the present paper was developed. The author visited the chapel several times, and measurements were taken. These dimensions were then compared with drawings from the archive.

Results Part I: Theory

Shapes used by Dom Bellot

Following a careful study of Dom Bellot texts and drawings we can conclude that he invented and used his own proportional system to create architectural spaces. Starting from very simple shapes he successfully links all the elements into one, harmonious whole. The shapes he employs the most are the Golden Triangle, the Pythagorean triangle, the square, and the so-called Egyptian triangle. Each of these are described hereafter.

The Golden Triangle

The Golden Ratio

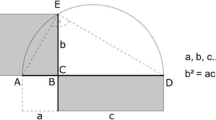
The “Golden Ratio” or phi (φ) was defined by Euclid in his treatise The Elements. He said: “A straight line AB is said to have been cut in extreme AC and mean ratio CB when, as the whole line is to the greater segment, so is the greater to the less.”

To express this proportion mathematically, we say: AB/AC = AC/CB, which gives (x + 1)/x = x/1, or x2 − x − 1 = 0, x = (1 + √5)/2 = 1.618034(φ) (see Figs. 5, 6).

Fig. 5
figure 5

Two graphical ways to draw the Golden Section. Drawing Dom Bellot. © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey Saint-Paul de Wisques

Full size image
Fig. 6
figure 6

Drawing by the author

Full size image

Dom Bellot gives two ways to express the Golden Ratio in a graphical way, depicted in Fig. 5; the first is to take a square of ratio 1:1 (ACGF), and to find the mid-point of one of the perpendicular sides. Then using the opposite perpendicular side, make a sloping line from its top corner F to dissect the opposite side. Continue the line out of the square and extend it until it meets where the baseline should be (point B)—as the aim is to form a triangle (GAB). The baseline of the square will then need to be extended to meet the point of the new sloping line (AB); the baseline of the square AC will be extend with his mean ratio CB.

The other way to show the Golden Ratio is to take two squares to make a rectangle where the height equals 1 and lower line equals 2. Let us call this lower line AB. We then draw a diagonal from the topmost right corner to A, in order to dissect the rectangle. We have a triangle. We place the compass point on the topmost right corner and the pencil at B, then swing an arc to the diagonal. Then, taking A as the new compass point, we swing an arc with the pencil to dissect the line AB, matching the arc of this new arc with the edge of first arc, exactly. The new dissection made on the line AB is called C. When measured, AB/AC = AC/CB, the result is φ.

Dom Bellot’s Mysterious Set Square, the Golden Triangle

It is certain that Dom Bellot used a set square unlike the standard right-angled set-square of 30° by 60°. His set square remained secret for the duration of his lifetime (Wintrebert 2007). Figure 7 shows that his set square was a triangle of 90° with opposing angles of 58°17′ and 31°43′. These two alternative triangle angles gives sides with the Golden Ratio relation; DP is the extreme ratio and DF is the mean ratio. This set square was a way to divide a surface according to the Golden Ratio.

Fig. 7
figure 7

The mysterious set square (PDF). Drawing by Dom Bellot. © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey St-Paul de Wisques

Full size image

To arrive at Bellot set square, the instructions are as follows (depicted in Fig. 8). As before, start with two squares where the height is equal to 1 and the lower line is equal to 2. He calls this lower line DP. He draws a diagonal from the top right hand corner to D, making a triangle. Using the top right corner as the compass point place the pencil tip at P and draw an arc to dissect the diagonal line (of the triangle) that has just been drawn. This intercept is called S. Draw a diagonal line from P to S, and extend it, well past the rectangle. Then extend the perpendicular of the rectangle (at the left hand side) and this will give you the Golden Triangle. The smaller angle is 31°43′ described by Dom Bellot as 1/φ. The other angle 58°17′ is described by Dom Bellot as φ.

Fig. 8
figure 8

Drawing by the author

Full size image

This set square is the starting point of Bellot practical application of dividing. That is, that the whole unit should be divided in ratios of the same type.

Dom Bellot’s Basic Ratios

Dom Bellot used his Golden Set square in relation to the ratio 1:2.

Figure 10, drawn by Dom Bellot, gives a combination of two squares and the Golden Rectangle. He starts from two squares to make a rectangle, with the height/width ratio 1:2. He dissects this 1:2 rectangle using the 1/φ angle of his Golden Set square. Where the diagonal dissects the top line, a new perpendicular is drawn vertically to meet the lower line. This gives a new base line which Dom Bellot re-names “1.000”. We will call this his first Basic Ratio (see Fig. 10).

From this point Dom Bellot draws a perpendicular to the diagonal of the Golden Rectangle. This gives a smaller Golden Rectangle with the same ratio as the original Golden Rectangle. This construction is also called the reciprocal rectangle in art literature. This construction is also used by Le Corbusier as l’angle droit, or the right angle (Bartlett et al. 2013; Huylebrouck 2014) (see Fig. 9).

Fig. 9
figure 9

A golden rectangle can be subdivided in a square and a rectangle proportional to the original rectangle. This right-angle construction was also used by Le Corbusier. Drawing by the author

Full size image

Proportionally, Dom Bellot re-names the base line of the original 1:2 rectangle as “1.237”. This gives his second Basic Ratio (see Fig. 10). To come to a third base line length, it seems that he works with the mirrored set square with slope 1/φ. This line cuts the extend base line in a point slightly further than the double square ratio 1:2. This gives his third Basic Ratio. Dom Bellot called this line “1.431”. The pencil lines in Fig. 10 give birth to a large number of ratios.

Fig. 10
figure 10

The basic ratios. Drawing by Dom Bellot. © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey Saint-Paul de Wisques

Full size image

What are these Basic Ratios given by Dom Bellot? How do we have to look at them?

If we analyse Fig. 10, his second Basic Ratio actually should be 2/φ = 1.236 and not 1.237 (see Fig. 12).

Dom Bellot also used his Golden Set square in relation to the circle and the rectangle √5, see Fig. 11.

Fig. 11
figure 11

Golden set square in relation to the circle and the pentagon. Drawing by Dom Bellot. © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey Saint-Paul de Wisques

Full size image

He gives ADx2.236 = DC = rectangle √5 = ABCD.

In this way his second Basic Ratio actually also can be found as √5 − 1 = 1.236.

If Dom Bellot mirrored the set square with slope 1/φ to come to his third Basic Ratio, then this ratio should be 1.447 instead of 1.431. This can be calculated as follows:

In Fig. 12 one can see two Golden Triangles, a big and a small one. The relationship between the two lengths of these triangles are proportionally the same or:

$$\begin{array}{llll}\, &1 - {\text{y}}/{\text{y}}/\varphi = {\text{y}}/\varphi /{\text{y}} = {\text{short leg}}/{\text{long leg}} \hfill \\ &1 - {\text{y}} = {\text{y}}/\varphi^{ 2} \hfill \\ &{\text{Y}} = \varphi^{ 2} /\varphi^{ 2} + 1 = \varphi + 1/\varphi + 2\hfill \\ &2 {\text{y}} = 2\varphi + 2/\varphi + 2 \approx 1. 4 4 7. \hfill \\ \end{array}$$
Fig. 12
figure 12

Drawing by the author

Full size image

Is Dom Bellot making a mistake? Or does he want to achieve something else?

How Dom Bellot used these Basic Ratios

In the archives of CAMT, one can find the composition of a bell tower (Fig. 13) drawn by Dom Bellot. Dom Bellot shows the use of his mysterious set square in this drawing, starting at the base and flipping upwards the height of the column three times. He started from the ratio 1.618 to determine the surfaces. He took the width of the tower column equal to a = 5.50. Then he calculated the height of his Golden Triangle d = 5.50 × 1.618. The height of the column is made up of three Golden Triangles or 3xd. He also used the Basic Ratio 1.236. This ratio is visible in the transition of the tower column to the roof, c = a/1.236.

Fig. 13
figure 13

Composition bell tower. Drawing by Dom Bellot. © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey St-Paul de Wisques

Full size image

He actually gives a fourth basic ratio namely 1.157. He determined b = a/1.157. This gives him two times the wall thickness by a − b. This new ratio can be found out of his basic ratios given in Fig. 10: 1.431/1.237 = 1.157. Dom Bellot used rectangular tracing to split up the figure into modules and simple ratios. He starts doubling the length or the width of the shapes. This creates a lot of freedom to make up a complex composition. In the composition of the weathercock one can see the use of l’angle droit, or the right angle construction.

The Right-Angled Triangle 3-4-5

This triangle, also called the Pythagorean triangle was already used in ancient times. A right-angled triangle with sides 3 and 4, gives a diagonal of 5. Dom Bellot corresponded with his brother, who lived in Spain and was also an architect, about his design system. In 1919, after the First World War, he received a letter from his brother in Oosterhout. In the annex of that letter one can find two sketches, shown in Figs. 14 and 15. Figure 14 gives a 3-4-5 triangle linked to the Golden Triangle (PDF) and the Egyptian triangle (E). In Fig. 14, the baseline of the Pythagorean triangle is divided in measure of 4 units (which can also be expressed as 8 × ½ measures). In this drawing the baseline is cut according to the Golden Section, or coupe d’or, into a larger section (GM = grand major) and smaller section (PM = petit major). The baseline is also divided into two parts, 5 and 3, which gives virtually the same result. Note that the points do not exactly coincide with the Golden Section, since 5/3 = 1.666 is significantly larger than φ.

Fig. 14
figure 14

The golden triangle (PDF, in red) in combination with the triangle of Pythagoras (Py) and the Egyptian triangle (E). Drawing in letter to Dom Bellot 1919 © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey Saint-Paul de Wisques

Full size image
Fig. 15
figure 15

Egyptian triangle (in blue) in combination with the triangle of Pythagoras (Py) (in red) and the Golden Triangle (black line PDF). Drawing in letter to Dom Bellot 1919 © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey Saint-Paul de Wisques

Full size image

The Egyptian Triangle

A third basic form is the Egyptian triangle. This triangle has a total base measuring eight units and a height of five units (Fig. 15). This triangle is also described by Viollet-Le-Duc (1854). The Dutch architect Berlage also constructed his Egyptian triangle on the basis of the ratio height: base = 5, 8 (Bax 2005). In 1909 Dom Bellot visited Amsterdam with Jan Stuyt (1868–1934), a former student of Joseph Cuypers (1861–1941). The façades of the Amsterdam Exchange (build by Berlage 1898–1904) are based on this Egyptian triangle. (Culot et al. 1996, pp. 37–41). In the late nineteenth and early twentieth centuries there was a wide diffusion in Holland of theosophy, for which the geometric was the essence of the real.

Figure 15 gives the second sketch that Dom Bellot received in a letter from his brother in 1919. In this drawing the Egyptian triangle is connected with the Pythagorean triangle. The hypotenuse with size 5 of the triangle of Pythagoras (drawn in red) is equal to the height of 5 units of the Egyptian triangle. Also the Golden Triangle (PDF) is drawn in the Egyptian triangle (E) These triangles were easy to distribute in modules.

As a remark on the use of the Egyptian triangle in Art, we make a reference to Herodotus (484?–425 BC). He noted that half the base is said to be the Golden Ratio of the slant height of the Egyptian triangle. (Figure 16) Or √φ:1 = 1.272… so 5:4 = 1.25 is a decent approximation.

Fig. 16
figure 16

Egyptian triangle and the relation with the golden mean

Full size image

The Square and the Double Square

A fourth basic shape is the square. The combination of a square and the square rotated by 45°, which gives an octagon, is another favourite form of Bellot (Fig. 17). If one divides the baseline and the height of the square into 10 parts (10 = 3 + 4 + 3), one can see the ratio 3-4-5 (red). In history the ratio 10:7 is used as a rational approximation of √2 (Fig. 18).

Fig. 17
figure 17

Square and rotated square by the author

Full size image
Fig. 18
figure 18

Rotated square producing a very close approximation to the ratio 3:4, drawing by the author

Full size image

In the private archive of Dom Bellot one can find a first draft of the cemetery chapel St. Adalbert (1922–1924) in Bloemendaal (Fig. 19). In this design Dom Bellot used a square and a square rotated by 45°. Dom Bellot divided the baseline of the square into 16 parts and the height of the square into 10 parts; one can see little rectangles with the Golden Ratio (green) (Fig. 20).

Fig. 19
figure 19

First draft of the cemetery chapel at Bloemendaal by Dom Bellot. © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey St-Paul de Wisques

Full size image
Fig. 20
figure 20

Analysis by the author

Full size image

The Construction of the Arch

Dom Bellot developed different arch forms. He wanted to create a sense of movement from one form to another, by way of his arches. The arch in fact connects all of the parts, to result in unity. Examples of his arch forms can be seen in Fig. 21, the interior of the chapel of the Augustinian college at Eindhoven. How did he build up this arch and the form of this dome?

Fig. 21
figure 21

The chapel of the Augustinian college at Eindhoven. Photo: author

Full size image

First the arch of the chapel is constructed out of a Golden Rectangle as given in Fig. 22. Dom Bellot made this arch by means of five starting points. He started with a Golden Rectangle. Then he draws a half circle in the Golden Rectangle with the centre point in the middle of the upper line of the rectangle. From the lowest point of this half circle one can draw a circle with radius the distance to the lower line of the Golden Rectangle. One can draw a second circle with the same radius in the middle point of the baseline. The combination of these two circles and two lines with a slope of angle 1/φ or 31°43′ gives two starting points on the baseline. The intersection of the two circles gives the next two starting points for the arch. From the intersection of the circles one can draw another two lines with slope φ or 58°17′. The intercept of these lines gives the fifth starting point (Figs. 22, 23).

Fig. 22
figure 22

Arch drawn in a golden Rectangle. Drawing by Dom Bellot. © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey St-Paul de Wisques

Full size image
Fig. 23
figure 23

Drawing by the author

Full size image

Secondly, the form of the dome is made out of a double square as shown in Fig. 24. He started with a ratio 1:2 under the spring line of the arch. The baseline of this rectangle can be seen as his first basic ratio 1.000. He draws the arc by means of five points: C and C′ are given by 1.236, the second basic ratio seen in Fig. 10. These are the endpoints of another 1:2 ratio. The starting points D and D′ are found by the points of intersection of the diagonals of the double square and single squares. The upper point E is found by drawing a line with an angle of 45° from D or D′ to the middle (Fig. 24). We will find this construction returns in the case study of the chapel (Fig. 25).

Fig. 24
figure 24

Arch drawn out of the double square. © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey St-Paul de Wisques

Full size image
Fig. 25
figure 25

Drawing by the author

Full size image

Results Part II: Analysis of the College and Chapel of the Augustinian Fathers at Eindhoven

In this section we will look at the proportional relationships in a case study of the chapel of the former Augustinian College built by Dom Bellot in 1922–1925. The Dutch architects Van de Leur and the young Pierre Cuypers junior were his assistants (Culot et al. 1996, pp. 85–86). The chapel is situated in the city centre of Eindhoven in The Netherlands (Fig. 26).

Fig. 26
figure 26

The Gymnasium Augustinianum along the Kanaalstraat and the chapel along the river de Dommel in Eindhoven © Bellot (1927) image 76

Full size image

Analysis of the Staircase of the Chapel

Figure 27 shows the ground plans of the staircase to the chapel. The width of the chapel is measured out, one can see 99 + 55 + 726 + 55 + 99 = 1034.

Fig. 27
figure 27

Ground plan of the staircase hall and entrance of the chapel in Eindhoven. Drawing Dom Bellot © ANMT Roubaix fonds Dom Bellot, property of: l’Abbey Saint-Paul de Wisques

Full size image

We can actually see the use of his Golden Section angle of almost 60° in combination with triangular tracing in his design of the cross-section of the staircase to the chapel. The pencil lines show the use of this Golden Section angle to build up the diverse arches (Fig. 28).

Fig. 28
figure 28

Ground plan of the staircase hall and entrance of the chapel in Eindhoven. Drawing Dom Bellot © ANMT Roubaix fonds Dom Bellot, property of: l’Abbey Saint-Paul de Wisques

Full size image

Analysis of the Plan of the Chapel

Figure 29 shows the ground plan of the chapel. The nave consists of three squares in succession; the staircase is a nine-square configuration.

Fig. 29
figure 29

Ground plan of the chapel in Eindhoven. Drawing Dom Bellot © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey Saint-Paul de Wisques

Full size image

Analysis of the Stained-Glass Window of the Chapel

In the stained-glass window can be seen an octagon created by the square rotated by 45° (Fig. 30). The baseline of this square is equal to 407 cm, and can be seen as the progression 3 × 132 (12 headers or 12 × 11). The total stained-glass window can be seen as a rectangle with a close relation to the ratio 3:4. The width of the stained-glass window is equal to 407 and the height is equal to 537.5 = 4 × 131.25 (21 courses) + 2 courses (12.5).

Fig. 30
figure 30

Cross section of the chapel showing the stained glass window of the chapel. Drawing by Dom Bellot. © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey St-Paul de Wisques

Full size image

Analysis of the Arches of the Chapel

In this cross-section of the chapel, one can also see the construction of the arch (Fig. 31). Dom Bellot starts from a Golden Rectangle with a width of 704 cm and a height of 437.5 cm. The graphical construction is the same as that given in Figs. 22 and 23.

Fig. 31
figure 31

Cross section of the chapel showing the construction of the arch. The construction is the same as given in Figs. 22 and 23. Drawing by the author in a drawing by Dom Bellot. © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey St-Paul de Wisques

Full size image

In the cross-section of the chapel one can see the construction of the dome (Fig. 32). Dom Bellot starts from the width of 704 cm. The two first starting points can be found by increasing this length by the Basic Ratio 1.236: 704 × 1.236 = 870.144. This gives a size of 870 as the baseline from a double square with the height of 435 cm. The diagonals of those squares give the other three starting points, as given in Figs. 24 and 25 (Fig. 33).

Fig. 32
figure 32

Cross section of the chapel showing the construction of the dome. The construction is the same as given in Figs. 24 and 25. Drawing by the author in a drawing by Dom Bellot. © CAMT Roubaix fonds Dom Bellot, property of: l’Abbey St-Paul de Wisques

Full size image
Fig. 33
figure 33

View of the chapel. © Bellot (1927–1928)

Full size image

Discussion

The proportional system of Dom Bellot was linked to his personal philosophy and his theology. Anchored in the Golden Section, his system was a way to achieve beauty and order of the highest, holiest and most harmonious order. This state in turn gives peace and unity. He wrote:“Le beau consiste dans une juste proportion des choses, c’est-à-dire une disposition, un ordre interne qui est pour l’ esprit, qui contemple derrière les impressions sensibles, harmonie et clarité.” [True beauty lies in the right proportions of things, as an internal order of the spirit, which enters our minds through our senses, with harmony and clarity (Bellot 1948, p. 101; Willis 1994)].

For Dom Bellot, proportion is the introduction of a common measure. This can be done geometrically or mathematically, but always in a logical, and spiritual or intellectual way. He also makes a distinction between proportions and dimensions. Dimensions—length, height or width—are simple sizes. Proportions are relative links between the parts, according to a certain law. The word “proportion” does not indicate repeating fixed laws, always the same but, on the contrary, using variable relationships to obtain a harmonious scale. He refers to the growth of plants and animals. According to Dom Bellot, God made everything with weights and measures, and beauty. We are therefore obliged to build in harmony with this creation (Bellot 1948, p. 103; Willis 1994).

In 1927 and 1928, Dom Bellot and Dom Van der Laan lived together in the Benedictine community in Oosterhout in the Netherlands. After the death of Dom Bellot, Dom Van der Laan wrote an article on Dom Bellot (Van der Laan 1949–1950). It is curious that Dom Bellot after his departure from Oosterhout didn’t maintain a relationship with Dom Van der Laan. Maybe because Dom Van der Laan treats the plastic number measures not as rational approximations tending towards an irrational Golden Mean limit, but as finite numerical values. During the rest of his life Dom Bellot warned his pupils against using his systems mechanically. He loathed the thought of younger architects thinking that they could simply apply the systems without careful judgment and careful nuance. Those views are all conveyed in his lectures to younger architects in Quebec, and in letters to Dom Côté in particular (Bellot 1933–1937). Dom Côté was a Canadian priest who learned the use of the Golden Section from Dom Bellot (Simmins 1997). This may explain why Dom Bellot makes no direct reference to Dom Hans Van der Laan. The influence of Dom Bellot on Dom Van der Laan is a topic that needs further investigation. In the book Dom Hans Van der Laan, Modern Primitive, Padovan (1994) quotes Van der Laan about the discovery of the plastic number. In the appendix A of this book Padovan quotes Van der Laan about the ratio 1:2 as a source of the plastic number, and in the appendix B Padovan investigates the parallels between the plastic number and the modulor. The influence of Dom Bellot on Le Corbusier, through August Perret or the Parisian avant-garde is another topic that needs further investigation.

Other research questions are: What is the meaning of form and proportion in the works of Dom Bellot? What is the meaning of the arch in the works of Dom Bellot? What is the geometrical construction and the evolution of this arch? Can they be compared to the arches made by Gaudi?

Conclusion

Dom Bellot created his own proportional system out of a variety of traditions ranging from Viollet-le-Duc to Berlage and other Dutch counterparts working at the turn of the twentieth century, and still others from the ancient traditions of the medieval masons, and the theories of Pythagoras.

Dom Bellot used a triangulated crossing system based on his Golden Set-square. He related this Golden Ratio with the ratios 1:2 and 4:3. Dom Bellot treats his Golden Set-square and the additive plastic relationships as rational approximations tending towards an irrational Golden Mean limit. He used this system to build up harmonious proportions so that the whole unit could be divided in smaller ratios for the same type. In this way he wanted to create a true and pure kind of beauty of the type that is seen in nature. Dom Bellot saw his system as a means to express his faith in the metaphysical world.