Impact of N on the Stacking Fault Energy and Phase Stability of FCC CrMnFeCoNi: An Ab Initio Study

Abstract

Interstitial alloying has become an important pillar in tuning and improving the materials properties of high-entropy alloys, e.g., enabling interstitial solid-solution hardening and for tuning the stacking fault energies. In this work we performed ab initio calculations to evaluate the impact of interstitial alloying with nitrogen on the fcc–hcp phase stability for the prototypical CrMnFeCoNi alloy. The N solution energies are broadly distributed and reveal a clear correlation with the local environments. We show that N addition stabilizes the fcc phase of CrMnFeCoNi and increases the stacking fault energy.

1 Introduction

High-entropy alloys (HEAs) or complex concentrated alloys (CCAs) based on 3d transition metals have attracted enormous attention, particularly due to their outstanding mechanical properties. The equiatomic CrMnFeCoNi alloy, often referred to as Cantor alloy,[1] shows a remarkable combination of strength and ductility.[2,3,4,5] In addition to modifying the composition via substitutional alloying,[6,7,8,9,10,11,12,13,14,15,16,17,18] interstitial alloying with, e.g., C or N turned out to be promising to further tune the materials properties. The impact of interstitial C atoms in HEAs has been investigated in several previous experimental studies.[10,16,19,20,21,22,23,24,25,26,27] For CrMnFeCoNi, the addition of C atoms increases the yield and ultimate strengths[19,23,25] while also impacting ductility. Enhanced yield and ultimate strengths are also found for interstitial-alloyed $\hbox {Cr}_{0.1}$ $\hbox {Mn}_{0.3}$ $\hbox {Fe}_{0.5}$ $\hbox {Co}_{0.1}$[10] and $\hbox {Cr}_{0.1}$ $\hbox {Mn}_{0.4}$ $\hbox {Fe}_{0.4}$ $\hbox {Co}_{0.1}$[24] without a critical reduction of ductility. For MnFeCoNi alloyed with Al, even the improvements of both strength and ductility are observed when adding C.[28] A recent experimental study[29] revealed that N-alloyed CrFeCoNi with a bimodal grain structure shows also improved strength and ductility, overcoming their trade-off relation. This all highlights the potential of interstitial alloying for improving the materials properties of 3d-transition-metal HEAs.

An important quantity which can be sensitive to the interstitial alloying elements and which is linked to the mechanical properties is the stacking-fault energy (SFE), which is also directly related to the face-centered cubic (fcc) and the hexagonal close-packed (hcp) phase stability. The SFEs of fcc austenitic steels, particularly of high-Mn steels, have empirically been known to correlate with their deformation behaviors.[30,31,32,33,34] SFEs for 3d-transition-element-based HEAs have been also experimentally measured[8,17,26,35,36,37,38] and computed based on ab initio simulations.[39,40,41,42,43,44,45,46,47,48,49,50,51] The impact of interstitial C alloying on SFEs of HEAs has also been addressed in experimental studies[10,16,19,20,24,25,26] as well as by a few ab initio simulations.[28,52]

Whereas for steels several works on the impact of N on the SFEs have been carried out,[53,54,55,56,57] similar studies for HEAs are rare. In particular for interstitial N the impact on the phase stability of HEAs such as for, e.g., fcc CrMnFeCoNi, is still not well understood. It is the main scope of the present work to explore the impact of N for this prototypical HEA.

A challenge for disordered alloys is that, unlike for pure metals and ordered alloys, each interstitial site can display a different local chemical environment and revealing thus a different solution energy depending on the specific local environment. Such local features are usually intractable by experimental techniques. A computational alternative for accurately studying the impact of interstitial alloying from an atomistic viewpoint are ab initio calculations. For interstitial alloying with C, a few ab initio calculations for CrMnFeCoNi-based HEAs have been reported recently.[28,52] A significant dependence of the C solution energies on the local chemical environments has been found, with variations being much larger as compared to typical thermal activation energies.[28,52] For interstitial N alloying, however, similar detailed studies regarding the impact on the phase stability and the SFE for the protypical fcc CrMnFeCoNi HEA are still lacking.

In the present study, we utilize ab initio calculations to close the previous simulation gap and investigate the impact of interstitial N atoms on the fcc–hcp phase stability and SFE for CrMnFeCoNi, similar as previously performed for C[52]. Both the fcc and the hcp phases of CrMnFeCoNi are modeled based on the supercell approach to evaluate the SFE. Solution energies of interstitial N atoms are computed for both phases and a large number of interstitial sites is considered to explore the dependence on the local environments around N atoms.

2 Computational Details

2.1 Supercell Models Without Interstitial N

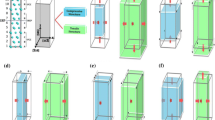
The CrMnFeCoNi HEA was modeled based on the supercell approach. To compute the SFE we considered the fcc and the hcp crystal structures (see Sect. 2.4 for details). To improve the computational accuracy, 54-atom fcc and hcp supercells are modeled with identical supercell shapes as shown in Fig. 1(a). The fcc unit cell is represented along the $\langle 111 \rangle$ direction as the third axis and displays the “ABCABC” stacking of the close-packed $\{ 111 \}$ layers, while the hcp unit cell has a “ABABAB” stacking of the close-packed $\{ 0001 \}$ layers. These supercells have six layers, and each layer consists of nine atoms. Ideal mixing of the elements in the five-component CrMnFeCoNi alloy was approximated utilizing the special quasirandom structure (SQS) technique.[58] For this purpose, the first and second neighbor pair correlation functions were optimized to be close to the ideal mixing state, i.e., the ideal random solid solution. In practice we constructed first two five-component SQS configurations, one for the fcc and the other for the hcp geometry. Then, for each SQS, $5! = 120$ supercell models can be obtained by permuting the order of the five elements. Note that the 54-atom SQS models have a composition ratio of 11:11:11:11:10, where one element is slightly deficient. For the interstitial N calculations (Sect. 2.2), 25 models from the set were selected, always 5 deficient in one of the 5 constituents, to obtain a fair representation of the equiatomic alloy. In the selected 25 models, 1350 octahedral and 324 tetrahedral sites for each phase were computed.

We previously evaluated the performance of 54-atom supercell models for the SFE of CrMnFeCoNi employing 120 configurations both for the fcc and for the hcp phases.[52] The computed SFE was similar to that reported in another previous computational study.[45] Moreover, a recent computational study[59] demonstrated for the case of FeNi that the mean SFE can be derived using a finite supercell as long as the statistical sampling is large enough.

2.2 Solution Energies of Interstitial Atoms

To compute solution energies for interstitial N, both octahedral and tetrahedral sites, which are surrounded by six and four atoms in the first nearest-neighbor (1NN) shell, respectively, were considered. Note that the octahedral and the tetrahedral sites in the fcc phase are from a geometric viewpoint very similar to those in the hcp phases, as visualized in Fig. 1(b). The solution energies $\varDelta E_\mathrm {sol}$ of N atoms in the dilute limit were computed as

$$\begin{aligned} \varDelta E_\mathrm {sol}&= E (\mathrm {alloy} + \mathrm {N}) - \left[ E (\mathrm {alloy}) + \frac{1}{2} E (\mathrm {N}_2)\right] , \end{aligned}$$

(1)

where $E (\mathrm {alloy} + \mathrm {N})$ and $E (\text {alloy})$ are the total energies of the alloys per simulation cell with and without an additional interstitial N atom, respectively, and $E (\mathrm {N}_2)$ is the energy of a $\hbox {N}_2$ molecule (cf. “Appendix).

As mentioned above, the interstitial sites in the considered disordered alloy reveal different local environments which results in different, local-environment dependent solution energies. Instead of a single value, the solution energy of N in a disordered alloy can therefore be described as a “density of states” (DOS) that satisfies¹

$$\begin{aligned} \int _{- \infty }^{\infty } n (\epsilon )\, d \epsilon&= N_\mathrm {site}, \end{aligned}$$

(2)

where $N_\mathrm {site}$ is the number of available interstitial sites, and $\epsilon = \varDelta E_\mathrm {sol}$.

The impact of $N_X$ interstitial atoms of the element X on the Helmholtz energy, $\varDelta F_\mathrm {sol}$, can be written as a function of temperature, T, as well as $N_X$, and can be separated as

$$\begin{aligned} \varDelta F_\mathrm {sol}(T, N_X) = \varDelta U_\mathrm {sol}(T, N_X) - T \varDelta S_\mathrm {sol}(T, N_X), \end{aligned}$$

(3)

where $\varDelta U_\mathrm {sol}(T, N_X)$ and $\varDelta S_\mathrm {sol}(T, N_X)$ are the contributions of the interstitial atoms to the internal energy and to the entropy, respectively.

To compute $\varDelta F_\mathrm {sol}$, the following two thermodynamic limits were considered[52]:

• 1. Ideal quenching condition: Interstitial atoms are assumed to occupy the interstitial sites fully randomly irrespective of their solution energies $\varDelta E_\mathrm {sol}$. This could be realized by, e.g., rapid quenching from high temperatures in which the interstitial atoms are “frozen” in their randomly distributed high-temperature state.

• 2. Ideal annealing condition: Interstitial atoms are assumed to occupy the interstitial sites according to the canonical ensemble for $\varDelta E_\mathrm {sol}$. This corresponds to the situation in which the disordered alloy is annealed for a sufficiently long time so that the interstitial atoms can diffuse into the thermodynamically favorable interstitial sites at a given temperature. Note that the alloy itself is still assumed to be ideally disordered.

In both the conditions, it is assumed that one interstitial site can be occupied by at most one interstitial atom and that there are no interactions between the interstitial atoms (dilute limit approximation).

In the ideal quenching condition, $\varDelta U_\mathrm {sol}(T, N_X)$ is written using the average solution energy $\overline{\varDelta E_\mathrm {sol}}$ over all interstitial sites as

$$\begin{aligned} \varDelta U_\mathrm {sol}(T, N_X)&= N_X \left( \frac{1}{N_\mathrm {site}} \int _{- \infty }^{\infty } n (\epsilon )\, \epsilon \, d \epsilon \right) \nonumber \\&= N_X \, \overline{\varDelta E_\mathrm {sol}}. \end{aligned}$$

(4)

Note that $\overline{\varDelta E_\mathrm {sol}}$ is independent of T and $N_X$. Further, since each interstitial atom is now assumed to be pinned to a certain interstitial site, $\varDelta S_\mathrm {sol}(T, N_X) = 0$. Thus, $\varDelta F_\mathrm {sol}(T, N_X)$ in the ideal quenching condition is given by

$$\begin{aligned} \varDelta F_\mathrm {sol}= N_X \, \overline{\varDelta E_\mathrm {sol}}. \end{aligned}$$

(5)

In the ideal annealing condition, an interstitial site is occupied with the probability given by the Fermi–Dirac distribution

$$\begin{aligned} f (\epsilon ; T, \mu )&= \left[ \exp \left( \dfrac{\epsilon - \mu }{k_\mathrm {B}T}\right) + 1 \right] ^{-1}, \end{aligned}$$

(6)

where $k_\mathrm {B}$ is the Boltzmann constant. The chemical potential $\mu = \mu (T, N_X)$ of the interstitial element in the alloy is determined for given T and $N_X$ to satisfy

$$\begin{aligned} \int _{- \infty }^{\infty } n (\epsilon )\, f (\epsilon ; T, \mu )\, d \epsilon&= N_X. \end{aligned}$$

(7)

Once $\mu (T, N_X)$ is self-consistently determined from Eqs 6 and 7, $\varDelta U_\mathrm {sol}(T, N_X)$ and $\varDelta S_\mathrm {sol}(T, N_X)$ are computed as

$$\begin{aligned} \varDelta U_\mathrm {sol}(T, N_X) = \int _{- \infty }^{\infty } n (\epsilon )\, f (\epsilon ; T, \mu )\, \epsilon \, d \epsilon , \end{aligned}$$

(8)

$$\begin{aligned} \varDelta S_\mathrm {sol}(T, N_X) = k_\mathrm {B}\int _{- \infty }^{\infty } n (\epsilon )\, s (\epsilon ; T, \mu )\, d \epsilon , \end{aligned}$$

(9)

$$\begin{aligned} s (\epsilon ; T, \mu ) = -\left[ f \ln f + (1 - f) \ln (1 - f) \right] , \end{aligned}$$

(10)

where $f = f (\epsilon ; T, \mu )$ ². Note for the ideal annealing condition, the alloy itself may also reveal, e.g., short-range order (SRO) and thus a different distribution of atoms as compared to the random solid solution. Consideration of these effects are beyond the present scope.

Thus obtained $\varDelta F_\mathrm {sol}$ was used to compute the impact of N atoms on the SFE, i.e., $\varDelta$SFE (cf. Sect. 2.4). Note that both in the high-temperature limit ($T \rightarrow \infty$) and in the high-concentration limit ($N_X \rightarrow N_\mathrm {site}$) in the ideal annealing condition, the $\varDelta$SFE equals to that in the ideal quenching condition.[52]

2.3 Local Environments Around Interstitial Atoms

To analyze the relation between $\varDelta E_\mathrm {sol}$ and the 1NN local environment around an interstitial N atom, we employed linear regressions of $\varDelta E_\mathrm {sol}$ based on the local valence-electron concentration (VEC), computed as the average of valence electron numbers over the six and the four atoms in the 1NN shell of an interstitial atom for octahedral and tetrahedral sites, respectively. The valence electron numbers of Cr, Mn, Fe, Co, and Ni were taken as 6, 7, 8, 9, and 10, respectively.

2.4 Stacking-Fault Energy (SFE)

In the present study, the SFE of fcc CrMnFeCoNi was computed based on the first-order axial Ising model (AIM1)[63] as

$$\begin{aligned} \text {SFE}&\approx \frac{2 (F^\text {hcp} - F^\text {fcc})}{A}, \end{aligned}$$

(11)

where $F^{\alpha }$ denotes the Helmholtz energy per simulation cell of the phase $\alpha$, A denotes the total areas of the close-packing layers in the simulation cell. This approximation may be intuitively understood because the fcc stacking faults locally have the same layer stacking as the hcp phase.

Under the AIM1 (Eq 11), the impact of $N_X$ interstitial atoms of the element X in the simulation cell on the SFE is computed as

$$\begin{aligned} \varDelta \text {SFE}&\approx \frac{2 \left( \varDelta F_\mathrm {sol}^\mathrm {hcp} - \varDelta F_\mathrm {sol}^\mathrm {fcc}\right) }{A}. \end{aligned}$$

(12)

where $\varDelta F_\mathrm {sol}^{\alpha }$ is the total contribution of the interstitial atoms to the Helmholtz energy of the phase $\alpha$. Note that in Eq 12, $N_X$ must be the same between the fcc and the hcp phases, i.e., no segregation of interstitial atoms on stacking faults is considered.

2.5 Electronic-Structure Calculations

The plane-wave basis projector augmented wave (PAW) method[64] was employed in the framework of density functional theory (DFT) within the GGA of the Perdew-Burke-Ernzerhof (PBE) form[65] as implemented in the VASP code.[66,67,68] The plane-wave cutoff energy was set to 400 eV. The Brillouin zones were sampled by a $\varGamma$-centered $4 \times 4 \times 4$ k-point mesh for the 54-atom supercell models, and the Methfessel-Paxton scheme[69] was employed with the smearing width of 0.1 eV. The 3d4s orbitals of Cr, Mn, Fe, Co, and Ni and the 2s2p orbitals of N were treated as the valence states. The total energies were minimized until they converge within 10$^{-3}$ eV per simulation cell for each ionic step.

For supercells without interstitial atoms, internal atomic positions were initially placed on the exact fcc and hcp lattice sites for the fcc and hcp supercell models, respectively. Ionic relaxations were performed until the residual forces became less than $5 \times 10^{-2}$ eV/Å. The volumes and the shapes of the supercells were kept fixed to the fcc lattice constant of 3.6 Å, which is close to the experimental value.[1,70,71,72,73,74,75] The ideal c/a ratio of $\sqrt{8 / 3} \approx 1.633$ was applied for the hcp phase, as in experiments[74,75] hcp CrMnFeCoNi revealed a c/a ratio close to the ideal one at ambient conditions.

All calculations were performed considering spin polarization. All the magnetic moments on Cr and Mn were initially set to be antiparallel to those on Fe, Co, and Ni, based on the results previously found using the coherent-potential approximation (CPA).[76] During the self-consistent calculations the local magnetic moments can adapt to their energetically preferred orientation, which is typically accompanied with spin-flips on the Cr and Mn sites, as discussed, e.g., previously in Ref.[52]

For each considered interstitial site, a N atom was first placed at the geometric center, and then the internal atomic positions are reoptimized.

3 Results and Discussion

3.1 Impact of N on Phase Stability and SFE

We first discuss the preference of interstitial N for tetrahedral and octahedral sites. We found that most N atoms initially placed at tetrahedral sites relaxed during the self-consistent calculations into neighboring octahedral or hexahedral sites. Only a small fraction of 13% and 17% for the fcc and the hcp phases, respectively, actually remained at the tetrahedral sites. This indicates that the vast majority of tetrahedral sites of CrMnFeCoNi tend to be dynamically unstable for N atoms. This is somewhat different to the case of interstitial C atoms for the same alloy reported previously,[52] where actually all C atoms initially inserted into tetrahedral sites of CrMnFeCoNi relaxed into neighboring octahedral or hexahedral sites. For N we also found that even the ones which remain in tetrahedral sites during the geometric optimization tend to show higher solution energies than those relaxed into the octahedral sites. This indicates that the tetrahedral sites are thermodynamically unstable for N atoms compared with the octahedral sites. In the following we therefore focus on the octahedral sites for the remaining discussion and analysis.

Fig. 1

(a) Simulation cells with 54 atoms for the fcc and the hcp phases. (b) Interstitial sites considered for N. Spheres in different colors represent different elements. Visualization is performed using the VESTA code[90]

Fig. 2

Distribution of computed solution energies $\varDelta E_\mathrm {sol}$ of interstitial N atoms at the octahedral sites in CrMnFeCoNi. The upper and the lower panels show the results for the fcc and the hcp phases, respectively. The average (avg.) and the standard deviation (SD) of $\varDelta E_\mathrm {sol}$ are also shown in the panels, and the impact of N on the SFE in the ideal quenching condition is shown in a box. The distribution for each phase is normalized to be integrated into one

Figure 2 shows the distribution of the computed solution energies $\varDelta E_\mathrm {sol}$ of the interstitial N atoms at the octahedral sites for the fcc and the hcp phases. The standard deviations of the $\varDelta E_\mathrm {sol}$ distributions are very similar, 0.337 eV and 0.335 eV for the fcc and the hcp phases, respectively. The differences between the highest and the lowest $\varDelta E_\mathrm {sol}$ are larger than 2.1 eV. This indicates that the local-environment dependence of $\varDelta E_\mathrm {sol}$ could have an impact on thermodynamic properties. The standard deviations of $\varDelta E_\mathrm {sol}$ distributions are also substantially larger than those obtained previously for C in CrMnFeCoNi (0.232 eV and 0.228 eV for the fcc and the hcp phase, respectively).[52] This indicates that the dependence of $\varDelta E_\mathrm {sol}$ on the local chemical environment is substantially larger for N atoms than for C atoms.

Among the considered 2700 octaheral sites, the lowest solution energy is found for the hcp lattice. It is important to note, however, that even with a number of 2700 configurations, we still consider a fraction of possible solution energies. The total number of possible configurations is, in principle, gigantic. If we assume that solution energies are affected by the first two nearest neighbors (6 nearest and 8 next-nearest neighbors for an octahedral site in fcc), there are for 5 components in principle more than 6 billion ($5^{6+8}$) possible configurations. The configuration space is narrowed down by focusing on a random alloy, which implicitly provides a preselection of local environments according to the probability present in the random solid solution. The local chemical phase space to be explored is, however, still huge. For this reason we resort next to the statistical analysis outlined in Sect. 2.2 and perform the different thermodynamic assessments. This statistical approach turned out to be more robust when considering the impact on the SFE.

In the ideal quenching condition (cf. Sect. 2.2), N atoms are equally distributed over all interstitial sites independent of the corresponding solution energies. In this scenario, the impact of N atoms on the SFE (Eq 12) is given by the difference of the average solution energy $\overline{\varDelta E_\mathrm {sol}}$ between the fcc and the hcp phases. As shown in Fig. 2, $\overline{\varDelta E_\mathrm {sol}}$ is by 0.135 eV lower in the fcc phase than in the hcp phase. This implies that, in the ideal quenching condition, N atoms energetically strengthen the fcc phase more than the hcp phase. Based on the AIM1 (Eq 12), an energy difference of 0.135 eV corresponds to a SFE change of 31 mJ/m² and 8 mJ/m² for 1 wt.% and for 1 at.% of N atoms, respectively. This is in the similar order to the impact of C atoms on the SFE of CrMnFeCoNi reported previously[52] (35 mJ/m² and 7 mJ/m² for 1 wt.% and for 1 at% of C atoms, respectively). The increase of the SFE due to N alloying for CrMnFeCoNi is qualitatively also similar to previous ab initio results for Fe and Fe-Ni,[57] while quantitatively the impact of N on the SFE is found to be much smaller in CrMnFeCoNi than for pure Fe reported previously[57] ($\approx$70 mJ/m² per 1 at% N).

In the ideal annealing condition (cf. Sect. 2.2), interstitial N atoms are distributed according to the canonical ensemble. To compute $\varDelta$SFE, we followed Eqs 6-10 with approximating the solution-energy DOS $n(\epsilon )$ in each phase by a Gaussian distribution. Figure 3 shows the thus computed $\varDelta$SFE in the ideal annealing condition at given T and $N_\mathrm {N} / N_\mathrm {site}$. The SFEs are found to be almost independent of T and to increase almost linearly with respect to $N_\mathrm {N} / N_\mathrm {site}$. For the same concentrations, the SFE shifts due to N in the ideal annealing conditions are almost identical to those in the ideal quenching conditions (31 mJ/m² and 8 mJ/m² for 1 wt.% and for 1 at.% of N atoms, respectively).

One can therefore conclude that interstitial N increases the SFE of the Cantor alloy, irrespective of the statistical treatment. The N impact is, however, much smaller than, e.g., for pure Fe.[57] The twinning behavior in the N-containing Cantor alloys is probably less affected and thus potentially less dominant for N-free Cantor alloys. This likely causes only a slight decrease of ductility. On the other hand, interstitial N would introduce solid solution strengthening, leading an enhanced yield strength. Indeed, this expected N impact is found in experiments for the $\hbox {Cr}_{0.1}$ $\hbox {Mn}_{0.3}$ $\hbox {Fe}_{0.5}$ $\hbox {Co}_{0.1}$ alloy containing interstitial C and N.[77]

3.2 Impact of Local Environment Around N

We next analyze the dependence of $\varDelta E_\mathrm {sol}$ on the local environment around the interstitial N atom in more detail. For the first qualitative measure, we focus on “M-rich environments” (M = Cr, Mn, Fe, Co, Ni) where the element M occupies half or more of the 1NN atomic sites around an N atom. Figure 4 shows the distributions of $\varDelta E_\mathrm {sol}$ for the M-rich local chemical environments. The distribution of $\varDelta E_\mathrm {sol}$ depends sensitively on the various local chemical environments. Cr-rich environments tend to show lower solution energies, followed by Mn-rich, Fe-rich, Co-rich, and Ni-rich environments. The low solution energies in Cr-rich environments indicate that N atoms in CrMnFeCoNi, if kinetically not prevented, are more likely occupying Cr-rich interstitial sites than other local chemical environments. This indicates that the Cr-N bonding is energetically the most favorable among the constituents, suggesting that Cr-N-rich precipitates are more likely forming as compared to other ones. Indeed, previous experimental studies reported $\hbox {Cr}_2$N precipitates for CrCoNi[78] and also for CrMnFeCoNi[79,80] when alloyed with N atoms.

Fig. 3

Impact of N atoms on the SFE in CrMnFeCoNi as a function of temperature T and concentration $N_\mathrm {N} / N_\mathrm {site}$ in the ideal annealing condition

Fig. 4

Distributions of the computed solution energies $\varDelta E_\mathrm {sol}$ of N atoms at octahedral sites in M-rich 1NN local chemical environments (M = Cr, Mn, Fe, Co, Ni) for the a fcc and the b hcp phases of CrMnFeCoNi

The trend in Fig. 4 implies that the solution energy of an N atom in CrMnFeCoNi is correlated with the local VEC in the 1NN shell of the N atom. In general, the relation between the VEC and the material-property of HEAs, including their phase stability, has been often discussed. Several previous papers found the correlation between the VEC and the bcc–fcc and the fcc–hcp phase stabilities.[81,82,83] Interesting correlations are found also for the local VEC around atoms. Atomic stresses in bcc refractory HEAs are also well predicted based on the local VEC around the atoms.[84]

Indeed, the correlation coefficients of $\varDelta E_\mathrm {sol}$ and the local VEC in the 1NN shell are found to be 0.845 and 0.848 for the fcc and the hcp phases, respectively, indicating strong correlations with $\varDelta E_\mathrm {sol}$ and the local VEC. These correlation coefficients for N in CrMnFeCoNi are much larger than those for C in CrMnFeCoNi obtained previously (0.511 and 0.597 for the fcc and the hcp phases, respectively).[52] The linear regressions of $\varDelta E_\mathrm {sol}$ based on the local VEC in the 1NN shell show root-mean-square errors (RMSEs) of 0.193 eV and 0.190 eV for the fcc and the hcp phases, respectively. The results of the present study suggest that for N the solution energies in CrMnFeCoNi can also be computationally very efficiently modelled utilizing the local VEC around the N atoms. Note that the strength of the correlation between the local VEC and the solution energy may depend on the crystal structure, the interstitial element, and the matrix constituents; for instance, the C solution energy in bcc TiVZrNbHf shows almost no correlation with the local VEC[85].

4 Conclusions

We studied interstitial N alloying for the prototypical CrMnFeCoNi high-entropy alloy (HEA) employing ab initio calculations. A wide range of chemically different local environments has been screened, namely 1350 and 324 different N configurations have been considered for octahedral and tetrahedral sites for both the fcc and the hcp phases. Based on a careful analysis of the extensive calculated data, a comprehensive representation and conclusion of the stability and energetical impact of interstitial N in CrMnFeCoNi could be obtained, namely:

• 1. Tetrahedral sites of CrMnFeCoNi are for N in most cases thermodynamically less favorable than octahedral sites.

• 2. The distribution of calculated interstitial N solution energies in the random alloy displays a width of larger than 2 eV. The large variation of solution energies reveals a strong dependence on the local chemical environment.

• 3. To evaluate the impact of N on the stacking fault energy (SFE), two thermodynamic scenarios are considered; one assumes a fully random occupation of N atoms irrespective of the solution energies in different local environments (ideal quenching condition), and the other assumes that N atoms are distributed according to a canonical ensemble for the solution energies (ideal annealing condition). In both the scenarios, the SFE increases by $\approx$31 mJ/m² and $\approx$8 mJ/m² for 1 wt.% and for 1 at.% of N, respectively.

• 4. N in CrMnFeCoNi is found to energetically prefer interstitial sites with lower local valence-electron concentration (VEC) as compared to C. The solution energies for N can be efficiently captured by considering the local VEC.

The strong dependence of N on the local chemical environment indicates that interstitial alloying with simultaneously controlling the total or local chemical composition (e.g., by introducing a certain degree of chemical short-range order (SRO) via tuning the annealing / cooling processing) could be a promising strategy to tune the SFE of HEAs further. The appearance of chemical SRO may be computationally addressed by Monte-Carlo-based approaches,[49,86] which can be combined with our methodology to study the impact of interstitial alloying. A strong dependence of N solution energies on local environments may not be limited to HEAs, but may also exist for other alloys like, e.g., Fe-Mn steels. It is therefore decisive, in contrast to pure metals, to comprehensively screen the phase space spanned by the different local chemical environments present in disordered alloys.

Appendix: Energy of \(\hbox {N}_2\)

In Eq 1, the energy of a $\hbox {N}_2$ molecule was computed with optimizing the bond length in a 20 Å$\times$20 Å$\times$20 Å simulation cell. The optimized bond length is 1.117 Å, while the experimental value is 1.09768(5) Å.[87]

A zero-point energy (ZPE) of 0.150 eV/molecule for $\hbox {N}_2$ was evaluated at the computationally optimized bond length within the harmonic approximation, in good agreement with the experimental value of 0.146 eV/molecule.[88]

The atomization energy of the $\hbox {N}_2$ molecule was also evaluated including the ZPE. The energy of a N atom was computed in a simulation cell with the same size as used for $\hbox {N}_2$. The thus computed atomization energy is 10.256 eV/molecule, while the experimental value at 0 K is 9.759 eV/molecule.[89] Thus, the $\hbox {N}_2$ atomization energy with the PBE functional is overestimated by 0.496 eV/molecule, which would affect the solution energies.

Note that this does not affect the impact of N on the SFE as computed in the present study, because any constant correction to the solution energy for the fcc and the hcp phases cancels out in Eq 12. For the sake of simplicity we computed the solution energy for N in Eq 1 referencing to the ab initio computed $\hbox {N}_2$ energy without ZPE.