Abstract
In this paper, we aim to study nonlinear time-periodic systems using the Koopman operator, which provides a way to approximate the dynamics of a nonlinear system by a linear time-invariant system of higher order. We propose for the considered system class a specific choice of Koopman basis functions combining the Taylor and Fourier bases. This basis allows to recover all equations necessary to perform the harmonic balance method as well as the Hill analysis directly from the linear lifted dynamics. The key idea of this paper is using this lifted dynamics to formulate a new method to obtain stability information from the Hill matrix. The error-prone and computationally intense task known by sorting, which means identifying the best subset of approximate Floquet exponents from all available candidates, is circumvented in the proposed method. The Mathieu equation and an n-DOF generalization are used to exemplify these findings.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The objective of this paper is to introduce a novel stability method based on the Hill matrix, which differs from the state-of-the-art methods in that a matrix projection is applied before computing an eigenvalue problem. The structure of this projection is obtained by considering the Hill matrix to be a result from the Koopman lift for well-chosen basis functions.
The Koopman framework [1, 2] has gained immense popularity in recent years as a versatile tool for various engineering applications, such as system identification [3], model order reduction [4] and feedback control [5]. This is due to an auspicious promise: global representation of a nonlinear system by a linear operator. To this end, in the Koopman framework, the dynamical system is defined through the propagation of functions on the state space, also called observables, over time. Bernard Koopman first described a unitary linear operator which evolves a class of measurable functions along the flow of a conservative system [6], which would later be named the Koopman operator. After some relatively quiet years, the Koopman operator experienced a revival around the turn of the century, when it was shown that its spectral characteristics contain global properties for the underlying dynamical system [7]. This sparked generalizations to non-conservative systems [8, 9] and at the same time, numerical and data-driven methods like the Arnoldi method [10] and extended dynamic mode decomposition [2] emerged.
Classically, the Koopman framework is applied to time-autonomous systems \({\dot{{\textbf{x}}}} = {\textbf{f}}({\textbf{x}})\) and the approximate linear dynamics obtained by the Koopman lift then takes the form \({\dot{{\textbf{z}}}} = {\textbf{A}}{\textbf{z}}\). The incorporation of a time-dependent input \({\textbf{v}}(t)\) into the dynamics, i.e., \({\dot{{\textbf{x}}}} = {\textbf{f}}({\textbf{x}}, {\textbf{v}}(t))\) or simply \({\dot{{\textbf{x}}}} = {\textbf{f}}({\textbf{x}}, t)\), generally poses problems in the Koopman framework as the system can only be approximated by a linear time-invariant (LTI) system \({\dot{{\textbf{z}}}} = {\textbf{A}}{\textbf{z}}+ {\textbf{B}}{\textbf{u}}(t)\) if products of state and input are neglected. In this paper we focus on non-autonomous systems for which the input is time-periodic, i.e., \({\textbf{v}}(t) = {\textbf{v}}(t + T)\). In particular, we propose a specific choice of observable functions which contains observables depending both on state and time, opening the possibility to include products of state and input.
The numerical computation of periodic solutions in time-periodic non-autonomous systems is a task of greatest interest in engineering application. Periodic solutions are of prime importance for, e.g., nonlinear vibration analysis in structural dynamics [11, 12], in acoustics [13] and thermo-acoustics [14], nonlinear oscillation analysis in electronic circuits [15] as well as heart rhythm analysis in cardiology [16]. Therefore, it is important to find and characterize periodic solutions, assess their stability properties and also track these quantities along varying system parameters, a process which is called continuation [17].
Naively, attractive periodic solutions can be found by simply simulating numerically over a long time interval, until transient effects are negligible. However, since this method is very dependent on the initial condition, can only find attractive solutions and is computationally expensive, more sophisticated methods have been developed. There are a multitude of periodic solution solvers available, including finite differences [18], shooting [19], multiple shooting [20], collocation and generalized collocation [21] and harmonic balancing [22]. We highlight two methods:
-
The shooting method [19] uses the Newton method and a numerical ODE solver to find initial conditions \({\textbf{x}}_0\) such that \({\textbf{x}}(t_0 + T) = {\textbf{x}}(t_0) = {\textbf{x}}_0\), i.e., whose trajectory over a period fulfills the periodicity constraint. Since the monodromy matrix appears in the update step of the Newton method, stability information comes (almost) for free with this method. This monodromy matrix also plays a role in the tangent prediction in an arc-length continuation method.
-
The harmonic balance method (HBM) [22, 23], in contrast to the other mentioned methods, is a purely frequency-based method. The periodic solution is parameterized globally by a finite set of trigonometric functions, and the coefficients are determined using a residual in the frequency domain. The transfer of nonlinear terms into the frequency domain is non-trivial. In practice, this is achieved either using an alternating frequency and time (AFT) method [24] or by providing a recast of the system in quadratic form [25]. One advantage of the HBM is that it automatically provides a filtering effect on the identified periodic solution.
While stability information about the periodic solution branches comes almost for free in the shooting methods as the monodromy matrix is calculated as a necessary continuation step, stability information and hence information about the bifurcations that occur in a system are not so trivial in the HBM. The Hill matrix provides a frequency-based method to assess the stability of periodic solutions [26, 27]. It can be found and constructed easily in the numerical asymptotic method (ANM) [25, 28], being a continuation method based on the HBM. Hence, computation of stability through its eigenvalues, which approximate the Floquet exponents, is a viable option.
However, two critical problems make the Hill method often unattractive in practice. On the one hand, from a numerical viewpoint, computing the eigenvalues of the large Hill matrix is computationally expensive and potentially inaccurate [29]. On the other hand, for correct assertion of stability, only a non-trivial subset of these eigenvalues must be considered. This process is known in the literature as sorting of Floquet exponent candidates. The determination of this subset is still an active area of research, with the approaches being based on the imaginary parts [23, 26, 30] and potentially in addition the real parts [31] of the eigenvalues, or alternatively symmetry considerations of the eigenvectors [27, 28].
In this work, we propose a different approach for obtaining stability information from the Hill matrix, which circumvents both issues mentioned above. Using the Koopman framework we motivate a novel dynamical systems interpretation of the Hill matrix, which allows to compute an approximation of the monodromy matrix directly (i.e., without computing a large number of eigenvalues and subsequent sorting). The proposed method to find the monodromy matrix from the Hill matrix involves the action of the matrix exponential of the Hill matrix applied to a smaller sparse matrix, followed by a projection to the \(n\times n\) monodromy matrix. Finally, the stability of the periodic solution can directly be assessed from the n eigenvalues of the monodromy matrix, known to be the Floquet multipliers.
Parts of the research in this work were presented in a preliminary form at the ENOC2020+2 Conference [32], in particular concerning the proposed choice of the Koopman basis functions in Sect. 3 and the connection to the harmonic balance equations and the Hill matrix. The main (and original) contributions of this work are the novel stability method of Sect. 4, the considerations with respect to the matrix projection and the formal proofs for the theorems in Sect. 3.2.
The paper is structured as follows. Section 2 provides an overview of the notation and gives a theoretical background for the concepts that are central to this work, in particular concerning a selection of topics from Koopman theory as well as frequency-based methods for periodic systems. Section 3 introduces the chosen basis for a Koopman lift on time-periodic systems and states the three central theorems which relate this Koopman lift to the classical frequency-based methods. The proofs of these theorems can be found in Appendix B. Section 4 presents the novel stability method based on the findings from Sect. 3, and the projection to the monodromy matrix as well as the computational effort are discussed. These results are illustrated in Sect. 5 using numerical investigations on two exemplary dynamical systems. Finally, concluding remarks are given in Sect. 6.
2 Theoretical background
In this section, the reader is provided with an overview over the theory in the Koopman framework and the Floquet theory that is necessary for the later parts of the paper.
2.1 Notation and terminology
The frequency-based methods considered in this work rely heavily on being represented as (generalized or classical) Fourier series. Hence, a short overview over Fourier series and the notation that is employed will be given.
Scalar quantities will be represented by Greek or Latin slanted lower case letters. This includes scalar-valued functions as elements of a function space. Vectors in Euclidean space will be represented by Latin bold lowercase letters and matrices will be represented by Latin bold uppercase letters. Tuples of functions are represented by bold font and the distinction to Euclidean space can be drawn from context.
The choice of index is connected to its meaning. The index \(l \in \mathbb {N}\) is used for indexing over the states of a system, whereas the index \(k \in \mathbb {Z}\) is used for indexing over frequency harmonics. While j may appear as arbitrary auxiliary index, the letter i usually denotes the imaginary number \({i^2 = -1}\) and is only used for indexing purposes if the indexing context is obvious. The Kronecker delta is denoted by \(\delta _{jl}\).
If an inner product \(\left\langle \cdot , \cdot \right\rangle \) with the usual inner product properties (see, e.g., [33]) is defined on a vector space \(\mathcal {F}\), elements \(f, g \in \mathcal {F}\) of this space are orthogonal if their inner product is zero. An orthonormal system is a set \(\left\{ \xi _j\right\} _{j = 1}^{D}, D \in \mathbb {N} \, \cup \left\{ \infty \right\} \) with \(\left\langle \xi _i, \xi _j \right\rangle = \delta _{ij}\), and a maximal orthonormal system whose span is a dense subset of the considered vector space is called an orthonormal basis.
By slight abuse of notation, the inner product is extended in this paper to tuples of functions \({{\textbf{g}}\in \mathcal {F}^l}\), \({{\textbf{h}}\in \mathcal {F}^m}\) element-wise via
It can be easily verified that, as a generalization of the conjugate symmetry of the inner product, the relation
holds, where \({\textbf{U}}^*\) denotes the conjugate transpose of the matrix \({\textbf{U}}\). Moreover, the sesquilinearity of the inner product extends to matrices via
for constant complex matrices \({\textbf{U}}, {\textbf{V}}\) of appropriate size.
If a space \(\mathcal {F}\) has an orthonormal basis \(\left\{ \xi _j\right\} _{j = 1}^{D}\) stacked into a tuple \(\varvec{\xi }\), it is well-known [33] that elements \(g \in \mathcal {F}\) admit a (generalized) Fourier series
where the matrix inner product notation was used in the last term. The constant, scalar coefficient \(\left\langle g, \xi _j \right\rangle \) is called the j-th Fourier coefficient of g. In particular, in the space of trigonometric functions of period T, the functions \(u_k: {[0~T) \rightarrow \mathbb {C}}, {t \mapsto \text {e}^{i k \omega t}},{ k \in \mathbb {Z}}\) constitute an orthonormal basis with respect to the inner product
This is the classical Fourier series. For a finite-dimensional subspace spanned by finitely many basis functions \(\left\{ u_k\right\} _{k = -N_{{\textbf{u}}}}^{N_{{\textbf{u}}}}\), a function g can thus be expressed by
with the matrix-valued inner product notation introduced earlier.
2.2 Koopman theory overview
A short introduction to the Koopman framework to set the notation and help the reader understand the following sections is given below. It is, however, not intended to give a comprehensive understanding of the current overall state of the art in the field that would be suitable for a wider range of application. For such a more general and in-depth treatment of the considered methodology, the authors rather recommend [10, 34].
Consider a non-autonomous time-periodic finite-dimensional dynamical system governed by
where \(t \in \mathbb {R}\) is the time, \({\textbf{x}}(t) \in \mathcal {X}\subseteq \mathbb {R}^n\) is the state trajectory starting at \({\textbf{x}}(t_0) = {\textbf{x}}_0\) and \({{\textbf{f}}: \mathcal {X}\times \mathbb {R}\rightarrow \mathcal {X}}\) is a smooth vector field which is T-periodic in t. The family of maps \({\varvec{\phi }_t({\textbf{x}}_0, t_0) = {\textbf{x}}(t)}\) characterizes the flow of the system and assigns to each (initial) configuration \(({\textbf{x}}_0, t_0)\) the resulting state at time \(t \ge t_0\).
The Koopman framework [10] considers output functions \(g({\textbf{x}}, t)\), also called observables. Any Banach spaces of functions over the complex or real numbers are permitted in the general Koopman framework. In this work, we consider in particular the space \(\mathcal {F}\) of complex-valued functions \(g: \mathcal {X}\times \mathbb {R} \rightarrow \mathbb {C}\) which are real analytic on \(\mathcal {X}\) and T-periodic in the last argument t. Given any function g, it may be of interest how its function values evolve along the trajectories of the system. For instance, in the Lyapunov framework, it is desired that function values of a Lyapunov candidate decrease over time for any starting point. The operator \(K^t: \mathcal {F}\rightarrow \mathcal {F}; g \mapsto g \circ \mathbf {\phi }_t\) performs this shift along the trajectory for arbitrary functions g from the considered function space. The family of all these operators for any t is called the Koopman semigroup of operators. Indeed, the semigroup properties with respect to the time parameter can be verified easily.
For suitable function spaces \(\mathcal {F}\), this Koopman semigroup contains all information about the system without explicitly knowing the vector field \({\textbf{f}}\) or the flow \(\varvec{\phi }_t\). In particular, if \(\mathcal {F}\) is chosen such that the identity function \(\textrm{id}\) is contained in the vector space, then the flow can be recovered easily by simply evaluating \(K^t(\textrm{id})\). As a trivial counterexample, consider the one-dimensional vector space of constant functions. Any constant function will not change its function value while being evaluated along an arbitrary trajectory of arguments. Therefore, in this case, the Koopman operator semigroup is well defined, albeit trivial. No information about the underlying system is retained. This example shows that an appropriate choice of function space is a crucial part of the Koopman framework.
Under the aforementioned assumptions for the particular function space \(\mathcal {F}\) and the vector field \({\textbf{f}}\), the Koopman semigroup is continuous with respect to time and there also exists the operator \(L: \mathcal {F}\rightarrow \mathcal {F}\ \hbox {with}\ g \mapsto {\dot{g}} = \lim _{t \rightarrow 0} \frac{K^tg - g}{t}\), mapping an observable g to its total time derivative \({\dot{g}}\) along the flow with
The operator L is called the infinitesimal Koopman generator. Again, for suitable \(\mathcal {F}\), this representation alone is a sufficient way to describe the behavior of the dynamical system. In particular, if \(\textrm{id} \in \mathcal {F}\), the vector field \({\textbf{f}}\) is easily recovered.
In addition, the infinitesimal Koopman generator and the Koopman semigroup of operators are linear in the argument g, even if the governing differential equation is nonlinear. This comes at the cost of dealing with a mapping on an (infinite-dimensional) function space \(\mathcal {F}\) instead of the (finite-dimensional) state space \(\mathcal {X}\).
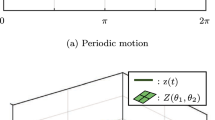
For practical reasons, we will be forced to project the dynamics on a finite-dimensional subspace \(\mathcal {F}_{{\hat{N}}} \subset \mathcal {F}\) spanned by \({\hat{N}}\) linearly independent basis functions \(\left\{ \psi _j \right\} _{j = 1}^{{\hat{N}}}\). Any projection \({\Pi _{{\hat{N}}}: \mathcal {F}\rightarrow \mathcal {F}_{{\hat{N}}}}\) defines a finite-dimensional approximation \({\hat{L}}: \mathcal {F}_{{\hat{N}}} \rightarrow \mathcal {F}_{{\hat{N}}}\) of L on \(\mathcal {F}_{{\hat{N}}}\) by \(L_{{\hat{N}}}:= \Pi _{{\hat{N}}} L\). The approximation process and the subsequent approximation error are visualized in Fig. 1. As the subspace \(\mathcal {F}_{{\hat{N}}}\) generally is not closed w.r.t. L, the result of Lg must be projected back onto \(\mathcal {F}_{{\hat{N}}}\), introducing some approximation error. As for \(\mathcal {F}\), the choice of the finite space \(\mathcal {F}_{{\hat{N}}}\) and the projection onto it is crucial.
To evaluate a system trajectory in the usual state-space form, the initial condition is fixed first, the state evolution is computed afterward and the output function is computed last. For the Koopman infinitesimal generator (and its approximation on the finite-dimensional function space), this is reversed. First, an observable, or output, is fixed, the observable is propagated along the flow and the initial condition is determined in the last step by evaluating \({(Lg)({\textbf{x}})}\) for an initial condition \({\textbf{x}}\). To arrive back at a linear system representation in the usual state-space form, this behavior must be reversed again. This is achieved by evaluating the action of the (approximate) Koopman infinitesimal generator on the basis functions. Setting
and keeping this dynamics for increasing t, the linear autonomous system
results. This linear system is called the Koopman lift and describes the dynamics represented in \(L_{{\hat{N}}}\). With the lifted states
it is a finite-dimensional linear approximation of the original system dynamics. The Koopman lift matrix \({\hat{{\textbf{A}}}}\) can be derived from the original nonlinear dynamics manually using a column vector \({\varvec{\Psi }}:= \left( \psi _1, \dots , \psi _{{\hat{N}}} \right) ^{\mathop {\textrm{T}}}\) of the basis functions of \(\mathcal {F}_{{\hat{N}}}\), computing \(\frac{\textrm{d}{\varvec{\Psi }}}{\textrm{d}t}\) and identifying terms linear in elements of \({\varvec{\Psi }}\) after applying the projection \(\Pi _{{\hat{N}}}\) from \(\mathcal {F}\) onto \(\mathcal {F}_{{\hat{N}}}\). If this projection is orthonormal and \({\varvec{\Psi }}\) is an orthonormal system, then the matrix entry \({\hat{{\textbf{A}}}}_{i, j}\) at i-th row and j-th column is given by \({\hat{{\textbf{A}}}}_{i, j} = \left\langle \frac{\textrm{d}\psi _i}{\textrm{d}t}, \psi _j \right\rangle \), where \(\left\langle ., . \right\rangle \) denotes the corresponding inner product.
Depending on the basis structure chosen, various popular embedding techniques emerge as a Koopman lift for specific system classes. For instance, if a monomial basis is chosen for an autonomous system, the Carleman linearization [35] results as Koopman lift. For smooth, polynomial systems, this is often the first choice of basis dictionary [36]. Alternatively, delay coordinates are often employed in Koopman-based applications [2]. Based on the Takens embedding theorem, this can capture weakly nonlinear dynamics [37]. For periodic systems, the Fourier embedding [38] has been known, although its properties have mainly been analyzed in the frequency domain.
2.3 Harmonic balance method
Consider the non-autonomous time-periodic finite-dimensional dynamical system (6) as above. Often one is interested in finding a T-periodic solution, i.e., a solution to the dynamical system (6) which fulfills \({\textbf{x}}(t + T) = {\textbf{x}}(t)\) for all \(t \ge 0\). This constitutes a boundary value problem (BVP) and there are methods to solve this type of BVP in the time domain and in the frequency domain. Shooting, multiple shooting and collocation methods all rely on an interplay between time-integration (or finite differencing) of the ODE and solving nonlinear functions for periodicity and continuity constraints [21].
In contrast, the HBM is a frequency-based method. Under suitable smoothness assumptions, the periodic solution has a convergent Fourier series. Hence the periodic solution can be approximated by its Fourier expansion up to order \(N_{\textrm{HBM}}\) with unknown parameters via
with \(\omega = \frac{2\pi }{T}\), \({\textbf{u}}(t) = (\text {e}^{- i N_{\textrm{HBM}} \omega t}, \dots , \text {e}^{i N_{\textrm{HBM}} \omega t})\) being a vector of Fourier base functions and \(\left\{ {\textbf{p}}_{-N_{\textrm{HBM}}}, \dots , {\textbf{p}}_{N_{\textrm{HBM}}}\right\} \) gathering the corresponding (unknown) coefficients. These coefficients \({\textbf{p}}_k\) are then determined by substituting this ansatz into the system equation (6). The comparison of coefficients for the Fourier expansions of \(\frac{\textrm{d}{\textbf{x}}_p}{\textrm{d}t}\) from the definition (10) and \({\textbf{f}}({\textbf{x}}_p, t)\) for every order up to \(N_{\textrm{HBM}}\) transforms the BVP into a system of \(n(2 N_{\textrm{HBM}} + 1)\) algebraic equations. Existence and convergence of these HBM approximations has been shown [22]. While the left-hand side of the equation as well as linear terms in \({\textbf{f}}\) are easy to handle, the frequency component of the nonlinear terms can usually not be expressed in closed form. The individual equations for each order are thus usually determined and simultaneously solved using the fast Fourier transform with an alternating frequency and time (AFT) method [24]. The equations for each order can also be isolated by projecting onto the corresponding basis function from the collection in \({\textbf{u}}\) through the classical inner product (4). Hence, the HBM approximates a periodic solution by solving the \(n(2N_{\textrm{HBM}} + 1)\) algebraic equations collected in
With this notation, the numerically cumbersome task of calculating the Fourier coefficients of the nonlinear components of \({\textbf{f}}\) is hidden in the definition of the inner product.
2.4 Floquet theory: stability of periodic solutions
When a periodic orbit \({\textbf{x}}_p\) is found (via HBM or by other means), the next interesting question is that of its stability properties; that is, whether trajectories that start sufficiently close to the periodic orbit will approach it, stay in a vicinity of it or tend away from it with increasing time. To evaluate the stability properties, the dynamics of a perturbation \({\textbf{y}}= {\textbf{x}}- {\textbf{x}}_p\) from the periodic solution is considered. Substitution of this definition into the original system dynamics yields
where \({\textbf{J}}(t) = \left. \frac{\partial {\textbf{f}}}{\partial {\textbf{x}}}\right| _{{\textbf{x}}_p(t), t}\) is the Jacobian of the system evaluated along the periodic solution. The approximate linear time-varying (LTV) system
has an equilibrium at zero, which corresponds to the periodic orbit of the original system, and the stability analysis of the periodic orbit reduces (in the hyperbolic case) to the stability analysis of this equilibrium. This will be the convention for the remainder of this paper, unless stated otherwise.
The fundamental solution matrix \({\varvec{\Phi }}(t)\) is the solution to the variational equation
and any state can be obtained via \({\textbf{y}}(t) = {\varvec{\Phi }}(t) {\textbf{y}}_0\). In particular, the fundamental solution matrix \({\varvec{\Phi }}(T)= :{\varvec{\Phi }}_T\) evaluated after one period is called the monodromy matrix of the system and its eigenvalues \(\{\lambda _l\}_{l = 1}^n\) are called Floquet multipliers [39]. The Poincaré map \({\textbf{y}}_{k+1} = {\varvec{\Phi }}_T {\textbf{y}}_k\) provides snapshots for the evolution of the perturbation \({\textbf{y}}\), spaced at a time distance of T, i.e., \({{\textbf{y}}_k= {\textbf{y}}(k T)}\). For the long-term behavior, it is sufficient to consider the evolution of these snapshots. Therefore, stability analysis of the periodic solution reduces to stability analysis of the Poincaré map. Hence, if all Floquet multipliers are of magnitude strictly less than one, the equilibrium of the perturbed LTV system and thus the periodic solution of the original system are asymptotically stable; if at least one eigenvalue has a magnitude strictly larger than one, they are unstable. If there exist Floquet multipliers with magnitude equal to one, but none with a magnitude larger than one, the equilibrium is non-hyperbolic and further investigation is necessary to give conclusive statements about stability of the originally considered periodic solution.
Alternatively to the Floquet multipliers, the stability properties of a time-periodic linear system can be characterized by the Floquet exponents. In the linearized perturbed system (13a), if the matrix \({\varvec{\Phi }}_T\) is diagonalizable, there exist n solutions \({\textbf{y}}_l(t) = {\textbf{p}}_l(t) \text {e}^{\alpha _l t}\) which form a basis of the solution space, where each function \({\textbf{p}}_l\) is T-periodic [39]. Hence, stability is characterized by the real parts of the Floquet exponents \(\{\alpha _l\}_{l = 1}^n\). If at least one Floquet exponent lies in the open right half plane, i.e., if at least one real part is larger than zero, the equilibrium is unstable. The Floquet multipliers can be determined by substituting \(t = T\) in the Floquet solution and it follows that
In contrast to the Floquet multipliers, the Floquet exponents are not uniquely defined. It is easy to see that if the pair \(({\textbf{p}}_l(t), \alpha _l)\) generates a solution \({\textbf{y}}_l(t)\), the same solution is generated by \(({\tilde{{\textbf{p}}}}_l(t), {\tilde{\alpha }}_l) = ({\textbf{p}}_l(t)\text {e}^{-ik\omega t}, \alpha _l + ik\omega )\) with \(k \in \mathbb {Z}\). Hence, in total, there are infinitely many valid Floquet exponents, which can be categorized into n distinct groups. All elements of one group have the same real part and differ in the imaginary part by multiples of \(i \omega \). As stability is determined by the real part only, it is sufficient for stability analysis to know any one element from each of the n groups. All elements of one group map to the same Floquet multiplier.
When a periodic orbit is determined using the purely time-domain-based shooting method, the monodromy matrix usually is a direct byproduct of the continuation method [17]. In this case, the numerically obtained monodromy matrix can be evaluated directly to obtain the Floquet multipliers and their stability information.
When the HBM is computed in the standard way, however, stability information about the identified limit cycle is unclear without further investigation. The Hill method [22, 40] offers a frequency-domain-based way to approximate the Floquet exponents of the linearized perturbation equation.
The Floquet exponents are eigenvalues of the infinite Hill matrix \({\textbf{H}}_\infty \) [30], which is constructed from the Fourier coefficients of the periodic system matrix \({\textbf{J}}(t) = \sum _{k = -\infty }^{\infty } {\textbf{J}}_k \text {e}^{i \omega k t}\) and reads as

Introducing a vector \({\textbf{v}}_{\infty }\) of appropriate (infinite) length, the eigenproblem
can be formulated. This infinite-dimensional problem has infinitely many discrete eigenvalues \({\tilde{\alpha }}\), which solve (17). They correspond identically to the Floquet exponents \({\tilde{\alpha }}\) for all \(k \in \mathbb {Z}\) as introduced above and can be sorted into n groups, where the entries of each group differ by multiples of \(i\omega \) [30]. However, in practice, only the eigenvalues of a finite-dimensional matrix approximation of \({\textbf{H}}_\infty \) can be computed numerically. The matrix
of size \(n (2 N_{{\textbf{u}}} + 1) \times n (2 N_{{\textbf{u}}} + 1)\) consists of the \({n (2 N_{{\textbf{u}}} + 1)}\) most centered rows and columns of \({\textbf{H}}_{\infty }\) and approximates the original infinite-dimensional Hill matrix. In the absence of truncation error, the eigenvalues of \({\textbf{H}}\) would be a subset of the eigenvalues of \({\textbf{H}}_{\infty }\), i.e., the Floquet exponents. Due to the inevitable error which generally comes with truncation, however, this does not quite hold. The N eigenvalues of \({\textbf{H}}\), which do not identically coincide with Floquet exponents, will be called Floquet exponent candidates below.
The matrix \({\textbf{H}}\) has a block Toeplitz structure except for the middle diagonal, and, for sufficiently large \(N_{{\textbf{u}}}\), the bands near the diagonal dominate as the Fourier coefficients of \({\textbf{J}}\) tend to zero. Loosely speaking, some eigenvalues affiliated most with the central rows of \({\textbf{H}}\) are less impacted by the truncation and provide a better approximation to the Floquet exponents than others [28]. Up until the change of the last century, this property was neglected and stability of the periodic solution was asserted based on the real parts of all Floquet exponent candidates [40]. This naive Hill method without any additional steps would often assert instability for stable solutions due to spurious Floquet exponent candidates without physical meaning, giving it a reputation of being inaccurate [22, 29].
However, the accuracy of the Hill method can be improved significantly if only a subset of Floquet exponent candidates is considered, instead of all of them. Hence, the search for a selection criterion which determines the best approximation to the Floquet exponents from the Floquet candidates has received much attention in the literature [23, 26, 28, 30].
For sufficiently large \(N_{{\textbf{u}}}\), it is proven that the candidates with minimal imaginary part in modulus converge to the true Floquet exponents [26]. Since the convergence may only occur for very large truncation orders, an addition to this method was very recently proposed [31]. This modified method first sorts the Floquet exponent candidates based on their real parts, before applying the imaginary part criterion to the most highly populated groups. However, in this real-part-based method, it is unclear how to proceed if two or more true Floquet exponents have the same real parts, and thus not enough groups are available.
An alternative criterion selects those candidates whose eigenvectors are most symmetric [27, 28], as they should correspond most to the middle rows of the matrix \({\textbf{H}}\). This symmetry is computed based on a weighted mean. Even though there currently is no formal convergence proof for this symmetry-based sorting method, some numerical results indicate faster convergence than with the aforementioned eigenvalue criterion [12], while other results do not support this claim [31].
For all these criteria, there are currently no methods to efficiently and accurately compute only those eigenvalues which fit the criterion. Rather, all eigenpairs of the large matrix have to be computed first and then most of them are discarded. As the cost of solving an eigenvalue problem of a \(N \times N\) matrix is of the order \(\mathcal {O}(N^3)\), the computational cost of the approach is usually dominated by determining the eigendecomposition of a large matrix [29]. In addition, it is well known that the accuracy of the computed eigenvalues is not too high if all eigenvalues of a sparse matrix are sought. Sparsity of \({\textbf{H}}\) cannot be reasonably exploited to decrease the computational cost of solving the complete eigenproblem [41].
3 A Koopman dictionary for time-periodic systems
For smooth autonomous systems in the Koopman framework, it is customary to choose as basis functions the so-called Carleman basis [2, 42], i.e., a finite set of monomials \(\psi _{\varvec{\beta }}({\textbf{x}}) = {\textbf{x}}^{\varvec{\beta }}\), where \({\varvec{\beta }\in \mathbb {N}^n}\) is a multi-index and standard multi-index calculation rules (see Appendix A) apply. As time-periodic functions are considered here, we propose in this paper to include as basis functions combinations of monomial terms as well as Fourier terms of the base frequency, i.e., basis functions of the form \(\psi _{\varvec{\beta }, k}:= {\textbf{x}}^{\varvec{\beta }} \text {e}^{i k \omega t}\), where \(\omega = \frac{2\pi }{T}\). The functions \(\left\{ \psi _{\varvec{\beta }, k} \vert k \in \mathbb {Z}, \varvec{\beta }\in \mathbb {N}_0^n \right\} \) are an orthonormal system within the initially considered vector space \(\mathcal {F}\) w.r.t. the inner product
This inner product contains the standard inner product for Fourier series, and the derivatives serve as an inner product for the monomials. The inner product properties can be readily verified.
Let \(N_{{\textbf{z}}}, N_{{\textbf{u}}} \in \mathbb {N}\) be integers which describe the assumed maximum polynomial and frequency order, respectively. There is a set \(\mathcal {B}= {\{\varvec{\beta }_j\}}_{j = 1}^{N_{\varvec{\beta }}}\) collecting all multi-indices with \(1 \le \left\| \varvec{\beta } \right\| \le N_{{\textbf{z}}}\). These are all multi-indices that create monomials \({\textbf{x}}^{\varvec{\beta }}\) of degree \(N_{{\textbf{z}}}\) and less. By (A4), it holds that \(N_{\varvec{\beta }} = \left( {\begin{array}{c}N_{{\textbf{z}}} + n\\ n\end{array}}\right) - 1\). For the sake of brevity, define \(N = N_{\varvec{\beta }}(2N_{{\textbf{u}}} + 1)\) and \({\hat{N}} = N + (2 N_{{\textbf{u}}} + 1)\). The set
of orthogonal basis functions spans a specific finite-dimensional subspace \(\mathcal {F}_{{\hat{N}}} \subset \mathcal {F}\). These basis functions are the monomials up to degree \(N_{{\textbf{z}}}\), multiplied to the Fourier base functions up to frequency order \(N_{{\textbf{u}}}\). With \({k = 0}\) and \({\left\| \varvec{\beta } \right\| = 1}\), the set (20) includes the identity function for each state. Moreover, since the multi-index \({\varvec{\beta }= \textbf{0}}\) is permitted in the set (20), the purely time-dependent classical Fourier base functions \(\text {e}^{i k \omega t}\) are represented. These basis functions are collected into two vectors. The vector
collects all basis functions that are not dependent on the state, but only on time, such that the evolution of \({\textbf{u}}\) is not a product of the system dynamics, but is known a priori. All other state-dependent basis functions are collected into the vector
Here, the basis functions are ordered by monomial exponent first, and then all frequency base functions for the same monomial are grouped together in ascending order. It is notable that any other orderings are also applicable and the matrices can be transformed into each other by similarity transforms. The ordering (22) has been chosen purely for convenience in later argumentation.
If the full basis as introduced above is considered, the state \({\textbf{x}}\) itself is included in the basis. Hence, there is a selector matrix \({\textbf{C}}_{{\textbf{z}}} \in \mathbb {R}^{n \times N}\) containing select rows of the identity matrix with \({\textbf{C}}_{{\textbf{z}}} {\varvec{\Psi }}_{{\textbf{z}}}({\textbf{x}}, t) = {\textbf{x}}\). There exist other options to recover \({\textbf{x}}\) from \({\varvec{\Psi }}_{{\textbf{z}}}({\textbf{x}}, t)\). For instance, monomials of higher (uneven) order can be used by considering the corresponding root. Also, the matrix \({\textbf{C}}_{{\textbf{z}}}\) can be allowed to be time-dependent. This second option and its implications will be investigated in more detail in Sect. 4.3. Both vectors \({\varvec{\Psi }}_{{\textbf{z}}}\) and \({\textbf{u}}\) are collected into one vector \({\varvec{\Psi }}:= ({\varvec{\Psi }}_{{\textbf{z}}}^{\mathop {\textrm{T}}}, {\textbf{u}}^{\mathop {\textrm{T}}})^{\mathop {\textrm{T}}}\) for convenience.
As introduced in Sect. 2.2, the Koopman lift describes the evolution of the basis functions under the approximate infinitesimal Koopman generator, and it is determined by expressing the time derivative along the flow of all basis functions in the finite-dimensional basis, projecting them back again to the subspace. Using the projection defined by the inner product (19), this gives
where \({\textbf{r}}\in \mathcal {F}^{{\hat{N}}}\) is the remainder that is orthogonal to the finite-dimensional subspace and will be projected out. Substituting (23) into the definition (9) for the Koopman lift and separating the two vectors of basis functions yields
where \({\textbf{A}}\in \mathbb {C}^{N \times N}\) and \({\textbf{B}}\in \mathbb {C}^{N \times (2N_{{\textbf{u}}} + 1)}\) are constant coefficient matrices. The lower rows of the large matrix in (24b) determine the dynamics of \({\textbf{u}}\). However, since \({\textbf{u}}\) is purely time-dependent and its time evolution is known a priori, the lower rows of (24b) are superfluous and the original nonlinear system is approximated by the LTI system
for the very specific input \({\textbf{u}}\) as in (21). The lifted state vector \({\textbf{z}}(t)\) is an approximation to the state-dependent basis functions \({\varvec{\Psi }}_{{\textbf{z}}}({\textbf{x}}(t), t)\) evaluated along the flow of the original system.
This is only an approximation, however, due to the projection onto the finite-dimensional function space. In particular, for \({t \ge 0}\), the lifted state \({\textbf{z}}\) will cease to adhere to the constraints posed by \({\varvec{\Psi }}_{{\textbf{z}}}\), meaning that there may not exist any vector \({{\tilde{{\textbf{x}}}} \in \mathbb {R}^n}\) which fulfills \({{\textbf{z}}(t) = {\varvec{\Psi }}_{{\textbf{z}}}({\tilde{{\textbf{x}}}}, t)}\).
Many results of this work tie in to classical results that are obtained from Jacobian linearization of the state space. Therefore, the maximum monomial order in the basis will often be restricted to \(N_{{\textbf{z}}} = 1\). In this case, the vector of basis functions will be denoted by \({\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}\) of size \({n (2 N_{{\textbf{u}}} + 1)}\) and for the sake of brevity, these functions will be called linear basis functions, even though the influence of time is still decidedly nonlinear. To make the ordering unique, these linear basis functions are ordered in an ascending order, first by state and then by frequency such that the resulting vector reads as
3.1 Koopman lift on the perturbed system
While a nonlinear dynamical system may have an arbitrary number of attractors of any kind (equilibrium, periodic, quasi-periodic, chaotic) located anywhere in the state space, the finite-dimensional linear Koopman lift (25a) has a very limited range of possible attractors, i.e., at most one single globally attractive solution, which is an equilibrium point. This means that the system (25a) will most likely not be able to describe the system dynamics of a nonlinear time-periodic system globally. For time-periodic systems, periodic solutions are expected. In this section, the Koopman lift of the perturbed system around such a periodic solution will be regarded to assess its local behavior.
As in the standard HBM, a periodic solution is approximated by its Fourier expansion (10) up to order \(N_{\textrm{HBM}}\) with unknown Fourier coefficients. The perturbed system is then given by \({{\textbf{y}}(t)= {\textbf{x}}(t) - {\textbf{x}}_p(t)}\), with dynamics
as in (12). This allows the Koopman lift to be performed on the perturbed system, i.e., on functions of the state \({\textbf{y}}\) evaluated along the flow \({\tilde{{\textbf{f}}}}\). Now, the origin of the lifted state does correspond to the origin equilibrium of the perturbed dynamics, or a periodic solution of the original dynamics. This also means that the Koopman lift matrices \({\textbf{A}}\) and \({\textbf{B}}\) now depend on the Fourier coefficients \({\textbf{p}}\) of the periodic solution around which we are linearizing. The following sections shed light on the properties of the matrices \({\textbf{A}}({\textbf{p}})\) and \({\textbf{B}}({\textbf{p}})\).
3.2 Koopman-based harmonic balance and Hill equations
One of our key findings is that the \({\textbf{B}}({\textbf{p}})\) matrix of the Koopman lift contains information about the parameterization of the periodic solution that is also encoded in the HBM. This is made more precise in the theorems given in this section.
Let \({\textbf{x}}_{p }= \sum _{k} {\textbf{p}}_k \text {e}^{i k \omega t}\) be a real-valued periodic solution candidate of the time-periodic system (6). The harmonic residual of this candidate is given by
Since \({\textbf{x}}_p\) as well as \({\textbf{f}}\) are periodic, the residual is periodic as well, and therefore it has a Fourier series
The HBM of order M returns solution candidates for which \({\textbf{r}}_k = 0\) for all \(\left| k \right| \le M\). Since \({\textbf{r}}\) is real-valued, it also holds that \({\textbf{r}}_{-k} = {\bar{{\textbf{r}}}}_k\), where \({\textbf{r}}_k = [r_{k, 1}, \dots , r_{k, n}]^{\mathop {\textrm{T}}}\) is a vector with n complex-valued entries.
This definition of the residual allows to concisely relate the HBM to the Koopman lift.
Theorem 1
Let \({\dot{{\textbf{z}}}} = {\textbf{A}}({\textbf{p}}) {\textbf{z}}+ {\textbf{B}}({\textbf{p}}) {\textbf{u}}\) be the lifted dynamics of frequency order \(N_{\textrm{HBM}}\) of system (6) around an unknown periodic ansatz of the form (10). The \(N_{\textrm{HBM}}\)-th order HBM equations (11), i.e., \({{\textbf{r}}_k \!=\! 0},\) \(\left| k \right| \le N_{\textrm{HBM}}\), are given by \({\textbf{C}}_{{\textbf{z}}} {\textbf{B}}({\textbf{p}}) = \textbf{0}\), where \({\textbf{C}}_{{\textbf{z}}}\) is the constant selection matrix that fulfills \({\textbf{y}}= {\textbf{C}}_{{\textbf{z}}} {\varvec{\Psi }}_{{\textbf{z}}}({\textbf{y}}, t)\) for all t.
The formal proof of this theorem is given in Appendix B.1. From an intuitive point of view, this condition is not surprising. For a periodic solution, the lifted dynamics has an equilibrium at zero, meaning that if \({\textbf{y}}= \textbf{0}\) it should also hold that \({\dot{{\textbf{y}}}} = \textbf{0}\). Since the lifted dynamics approximates \({\textbf{z}}(t) \approx {\varvec{\Psi }}_{{\textbf{z}}}({\textbf{y}}, t)\) and this approximation holds identically at the initial point (25b), it should hold that \({\dot{{\textbf{y}}}} \approx {\textbf{C}}_{{\textbf{z}}} {\dot{{\textbf{z}}}}\) is zero if \({\textbf{y}}= \textbf{0}\). This equation can be evaluated for an arbitrary initial point on the periodic ansatz via a time-shift. With \({\textbf{y}}(0) = \textbf{0}\) and \({\textbf{z}}(0) = {\varvec{\Psi }}_{{\textbf{z}}({\textbf{y}}(0), 0)} = \textbf{0}\), it turns out that the only remaining summand in the approximate \({\textbf{y}}\)-dynamics is \({\textbf{C}}_{{\textbf{z}}} {\textbf{B}}({\textbf{p}})\).
If only basis functions that are linear in the state (\(N_{{\textbf{z}}} = 1\)) are considered, the above result still holds. Moreover, we can state Theorem 2 about all entries of \({\textbf{B}}\) and not just specific rows.
Theorem 2
Let \({\dot{{\textbf{z}}}} = {\textbf{A}}({\textbf{p}}) {\textbf{z}}+ {\textbf{B}}({\textbf{p}}) {\textbf{u}}\) be the lifted dynamics of system (6) with linear basis functions \({\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}\) of frequency order \(N_{{\textbf{u}}}\) that are sorted as in (22), evaluated for the perturbed system around an unknown periodic ansatz of the form (10) up to frequency order at least \(N_{\textrm{HBM}} = 2N_{{\textbf{u}}}\). Then, the matrix \({\textbf{B}}({\textbf{p}}) \in \mathbb {C}^{n (2 N_{{\textbf{u}}} + 1) \times (2 N_{{\textbf{u}}} + 1) }\) consists of n stacked Toeplitz matrices. The l-th Toeplitz matrix \({\textbf{B}}_l\) contains as entries (ignoring duplicates) precisely the \(4N_{{\textbf{u}}}+1\) residuals \(r_{k, l}({\textbf{p}}), \left| k \right| \le 2N_{{\textbf{u}}}\) that follow from the HBM w.r.t the l-th state.
If \({\textbf{B}}({\textbf{p}}) = {\textbf{0}}\), then all these residuals of the HBM vanish. Conversely, if \({\textbf{p}}\) solves the HBM equations \({{\textbf{r}}_k({\textbf{p}}) = \textbf{0}}, {\left| k \right| \le 2N_{{\textbf{u}}}}\), then it holds that \({\textbf{B}}({\textbf{p}}) = \textbf{0}\).
The formal proof of this theorem is given in Appendix B.1.
In addition to the \({\textbf{B}}\) matrix, the \({\textbf{A}}\) matrix of the Koopman lift also holds frequency information about stability of the periodic solution. This is summarized in the following theorem.
Theorem 3
Let \({\dot{{\textbf{z}}}} = {\textbf{A}}({\textbf{p}}) {\textbf{z}}+ {\textbf{B}}({\textbf{p}}) {\textbf{u}}\) be the lifted dynamics around a periodic solution of system (6) with linear basis functions \({\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}\) of frequency order \(N_{{\textbf{u}}}\) that are ordered as in (22). Then the Hill matrix \({\textbf{H}}\), truncated to frequency order \(N_{{\textbf{u}}}\), for the periodic solution parameterized by \({\textbf{p}}\) results from the matrix \({\textbf{A}}({\textbf{p}})\) by the similarity transform \({\textbf{H}}= {\textbf{U}}{\textbf{A}}({\textbf{p}}) {\textbf{U}}^{\mathop {\textrm{T}}}\), where \({\textbf{U}}\) is an orthogonal permutation matrix that satisfies \({\textbf{U}}{\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}} = ({\textbf{y}}^{\mathop {\textrm{T}}}\textrm{e}^{i N_{{\textbf{u}}} \omega t}, \dots , {\textbf{y}}^{\mathop {\textrm{T}}}\textrm{e}^{- i N_{{\textbf{u}}} \omega t})^{\mathop {\textrm{T}}}\).
The formal proof of this theorem, again based on explicit evaluation of the inner product in the Koopman lift, is given in Appendix B.2.
With the three above theorems, qualitative insight about the accuracy of the presented Koopman lift can be gained. Locally (in the vicinity of a periodic solution), the lifted system contains the same dynamical information that is encapsulated in the Hill matrix of the same frequency order. Convergence results about the HBM [22] and the Hill method [26] can thus be related to the accuracy of the Koopman lift. Within the applied Koopman community, such a link is quite unusual. For many applications, convergence results for the finite-dimensional Koopman lift do not exist at all. The convergence results that do exist (e.g., [43, 44]) state that, under special conditions, a given error tolerance can be reached using a large number of specific basis functions, without giving an explicit upper bound. Hence, for time-periodic systems of the form (6), the proposed class of basis functions is a favorable choice due to its added connection with the Hill matrix, which indicates that the Koopman lift retains valuable stability information.
4 Sorting-free stability method
The Koopman lift with Theorems 2 and 3 gives a dynamical systems interpretation for the Hill matrix, allowing for a novel stability method based on the Hill matrix. This is demonstrated in the following section.
4.1 Approximating the monodromy matrix
Consider the Koopman lift as in Theorems 2 and 3, i.e., consider the linear basis \({\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}\) evaluated for the perturbed system around a periodic solution which is determined up to a frequency order of \(2 N_{{\textbf{u}}}\). From Theorem 2, we know that \({\textbf{B}}= \textbf{0}\) and from Theorem 3, that \({\textbf{A}}= {\textbf{U}}^{\mathop {\textrm{T}}}{\textbf{H}}{\textbf{U}}\). The linear dynamical system \({\dot{{\textbf{z}}}} = {\textbf{A}}{\textbf{z}}+ {\textbf{B}}{\textbf{u}}\) resulting from the Koopman lift therefore reduces to
where \({\textbf{C}}(t) \in \mathbb {C}^{n \times N}\) is a possibly time-dependent projection matrix that satisfies \({{\textbf{C}}(t) {\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}({\textbf{y}}, t) = {\textbf{y}}}\) for all \(t \in [0, T)\). There is a \(nN_{{\textbf{u}}}\)-parameter family of choices for \({\textbf{C}}\) if it is allowed to be time-dependent, which will be investigated further in Sect. 4.3. However, the naive choice would be to pick the entries in (26) that correspond to frequency zero. In this case, the matrix \({\textbf{C}}\) is constant and given by
where \({\textbf{I}}_{n \times n}\) is the \(n \times n\) identity matrix, \(\otimes \) denotes the Kronecker product and the second matrix in (31) is a row vector \(\in \mathbb {R}^{2 N_{{\textbf{u}}} + 1}\) with zeros everywhere except for the middle column.
Since for \(t = 0\) all exponential terms are 1 and vanish in (26), the vector \({\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}({\textbf{y}}, 0)\) can be expressed as a matrix product
for all \({\textbf{y}}\). The matrix \({\textbf{W}}\in \mathbb {R}^{N \times n}\) consists of (repeated) rows of the identity matrix. More specifically, it can be expressed as
where the second matrix in (33) is a column vector \(\in \mathbb {R}^{2 N_{{\textbf{u}}} + 1}\) filled with ones. As the system (30a)–(30c) is a linear time-invariant (LTI) system (except for the possibly time-dependent matrix \({\textbf{C}}\)), its closed form solution can be explicitly computed as
As a key finding of the current paper, the matrix \({\textbf{C}}(t) \text {e}^{{\textbf{A}}t} {\textbf{W}}\in \mathbb {R}^{n \times n}\) is an approximation of the fundamental solution matrix \({\varvec{\Phi }}(t)\), which is the matrix that satisfies \({\textbf{y}}(t) = {\varvec{\Phi }}(t) {\textbf{y}}(0)\). In particular, for \(t = T\), the monodromy matrix is approximated via
If the Hill matrix \({\textbf{H}}\) is already known due to other computations, e.g., as a by-product of a frequency-based continuation method such as MANLAB [27], then the similarity transform can be substituted into the matrix exponential to yield
where \({\tilde{{\textbf{C}}}}, {\tilde{{\textbf{W}}}}\) can also be computed directly via
by making use of the permutation properties of \({\textbf{U}}\) (see Thm. 3). The naive choice for \({\tilde{{\textbf{C}}}}\) was employed here for demonstration purposes, although all other choices are also applicable. Equations (35)–(37b) show that the choice of basis function ordering, and thus the exact numerical contents of the matrix, differ only formally and can be easily transformed into each other. For the sake of clarity, only the approximation (35) will be used in the following sections, unless otherwise stated. All results can, however, be transferred analogously to the formulation (4.1).
4.2 Stability and computational effort
As (35) is an approximation of the monodromy matrix, the Floquet multipliers can be approximated by its eigenvalues. This constitutes a novel projection-based stability method based on the Hill matrix. It is labeled sorting-free because the approach does not use the same steps as standard stability methods based on the Hill matrix [28, 30, 31].
In all standard approaches, the complete set of eigenvalues of the Hill matrix are determined in the first step. This is a computationally intense operation which may lack accuracy [41]. The result of this first operation is \(N = n(2 N_{{\textbf{u}}} + 1)\) Floquet exponent candidates, of which only n are the best approximations to the true Floquet exponents. There are various sorting algorithms that vary in computational expense, which aim to find these n best approximations as introduced in Sect. 2.4.
In contrast to these approaches, we now propose a sorting-free method. The Hill matrix is constructed identically to the aforementioned approaches. However, once the Hill matrix is obtained, the sorting-free projection-based stability method goes a different route. The approximation to the monodromy matrix is determined first via (35). In the most general case, a matrix exponential is of the same complexity range \(\mathcal {O}(N^3)\) as an eigenvalue problem [41, 45], however this is not the case for the specific operations presented here. We give two reasons:
-
1.
The matrix exponential in (35) is always multiplied by the matrix \({\textbf{W}}\), which is smaller and relatively sparse. The matrix exponential can thus be computed by multiple evaluations of the action of the matrix exponential on a sparse vector. For this operation, efficient scaling and squaring approaches which utilize these properties exist [46].
-
2.
In many applications the constructed Hill matrix will be relatively sparse. This is the case if the frequencies of the dominant harmonics of the original system are small in comparison to the frequency order. This sparsity in \({\textbf{H}}\), or equivalently in \({\textbf{A}}\), can be exploited in the scaling and squaring algorithm, in addition to sparsity in \({\textbf{W}}\).
As a second step in the sorting-free approach, it remains to solve an eigenvalue problem for the approximation of \({\varvec{\Phi }}_T\). This matrix is only of the size \(n \times n\), i.e., in general much smaller than the size \(n(2 N_{{\textbf{u}}} + 1) \times n(2 N_{{\textbf{u}}} + 1) \) of the Hill matrix \({\textbf{H}}\). The result are n Floquet multipliers and no a posteriori sorting of candidates is necessary. The reduction of candidates is performed implicitly by the projection matrices \({\textbf{C}}\) and \({\textbf{W}}\). This reduction through projection is essentially different from sorting, as the resulting Floquet multipliers from the projection-based method do generally not coincide identically with any Floquet multiplier candidates obtained as eigenvalues of the Hill matrix, transformed from Floquet exponents to Floquet multipliers via (15).
Alternatively to the Hill matrix approaches, the monodromy matrix can be determined via time-integration of the variational equation (14) [29]. Afterward, it again remains to solve the eigenvalue problem on the \(n \times n\) monodromy matrix. The three general approaches are visualized in Fig. 2. While the starting point for the novel method is the Hill matrix as in the standard Hill methods, the final steps of our method are instead identical to the time-integration method. However, the second indicated step, which needs the most computational effort in all three approaches, is different. The presented sorting-free projection method therefore has the advantage of being a Hill-based method, which is favorable in an HBM setting, and at the same time only requiring to compute the smaller eigenvalue problem of the monodromy matrix, similar to the time-integration-based method.
4.3 Choice of projection matrix
Until now, it has been established that \({\textbf{C}}(T) \text {e}^{{\textbf{A}}T} {\textbf{W}}\) approximates the monodromy matrix if \({\textbf{C}}{\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}} = {\textbf{y}}\). However, the choice of the matrix \({\textbf{C}}\) to achieve this is not unique. In addition to the naive choice (31), many more matrices are admissible. Recall that the vector \({\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}\) (26) is sorted such that it contains n consecutive blocks of length \(2 N_{{\textbf{u}}} + 1\), each block collecting all functions of a single state. Therefore, the l-th row of \({\textbf{C}}\), which singles out the l-th state, consists of \(n-1\) blocks of zeros, each of length \(2 N_{{\textbf{u}}} + 1\), and one block \({\textbf{c}}_l(t) \in \mathbb {R}^{1 \times (2 N_{{\textbf{u}}} + 1)}\) that is possibly filled with nonzero entries, yielding a non-square block-diagonal structure
with \({\textbf{c}}_l(t) \in \mathbb {C}^{1 \times (2 N_{{\textbf{u}}}+1)}; l = 1, \dots , n\). With this notation, the requirement \({{\textbf{C}}(t) {\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}({\textbf{y}}, t) = {\textbf{y}}}\) for all \(t \in [0, T]\) can be simplified to
by noting that \(y_l\) can be pulled out on both sides of the equation. As all entries in \({\textbf{u}}\) are linearly independent, the time dependency of \({\textbf{c}}_l\) is uniquely given via
to cancel out the time dependency in (39), such that \({\textbf{V}}(t) {\textbf{u}}(t)\) is constant. In this expression, \({{\hat{{\textbf{c}}}}_l \in \mathbb {C}^{1 \!\times \! (2 N_{{\textbf{u}}}\! +\! 1)}}\) is a constant row vector and \({\textbf{V}}(t)\) is given by \({\textbf{V}}(t) = {\mathop {\textrm{diag}}}{\left( \text {e}^{i N_{{\textbf{u}}} \omega t}, \dots ,\right. }\) \(\left. \text {e}^{- i N_{{\textbf{u}}} \omega t}\right) \). Due to (39) and \({\textbf{y}}\) being real, two additional conditions on \({\hat{{\textbf{c}}}}_l\) are
All choices for \({\hat{{\textbf{c}}}}_l\) that satisfy these conditions are admissible for the projection matrix. If a set \({\left\{ {\hat{c}}_{l, k} \right\} }_{k=1}^{N_{{\textbf{u}}}}\) of \(N_{{\textbf{u}}}\) arbitrary independent complex positive-frequency coefficients is given, they can be easily extended to an admissible choice \({\hat{{\textbf{c}}}}_l\) using the conditions (41), which implies that the admissible projection matrices form a \(nN_{{\textbf{u}}}\)-parameter family. For the sake of readability, the constraints will be left explicit in the considerations below. In Fig. 6–8 of Sect. 5.2, two choices for \({\hat{{\textbf{c}}}}\) are compared and it turns out that this choice indeed strongly influences the approximation quality.
For numerical computations, handling the sparse matrix \({\textbf{C}}\) with only few unknown coefficients is cumbersome. It is easier to collect all unknown variables \({\hat{{\textbf{c}}}}_l, l = 1, \dots , n\) into a long row vector \({\hat{{\textbf{c}}}}_{\textrm{all}}\) with
If the true monodromy matrix \({\varvec{\Phi }}_T\) would be known, then (35) can be viewed as a fitting problem for the unknown \({\hat{{\textbf{c}}}}_\textrm{all}\). The squared matrix residual
should be minimized. Setting \({\textbf{Q}}= \text {e}^{{\textbf{A}}T} {\textbf{W}}\) and utilizing the block diagonal structure (38) of \({\textbf{C}}(T)\), this expression decouples row-wise into n (nonlinearly) constrained least-squares problems
for \(l = 1, \dots , n\). In this equation, the matrix \({\textbf{Q}}\in {\textbf{C}}^{n (2 N_{{\textbf{u}}}+1) \times (2N_{{\textbf{u}}}+1)}\) is divided into n square blocks and due to the diagonal structure of \({\textbf{C}}(T)\), only the l-th block of \({\textbf{Q}}\) influences the l-th row of the least-squares problem (43). A matrix \({\textbf{C}}\) that was determined for comparison purposes using this least-squares problem under knowledge of the true monodromy matrix will be referred to as \({\textbf{C}}_{\textrm{true}}\) below. This least-squares problem has n equations for \(N_{{\textbf{u}}}\) independent unknowns. Therefore, to enable an optimal solution, it is advisable that the frequency order \(N_{{\textbf{u}}}\) is chosen to be at least n.
As the aim of this method is approximating the true monodromy matrix, which is unknown in applications, the least-squares problem (44) cannot be utilized in practice. As a practicable condition, the matrix \({\textbf{C}}(t)\) can be chosen such that it optimally satisfies the variational equation (14). The residual of (14) for the approximated fundamental matrix is
and a cost function can be defined via
Similarly to the block-based approach for the least-squares problem, this function with a matrix argument can be transformed into a quadratic cost function
with the vector \({\hat{{\textbf{c}}}}_{\textrm{all}}\) as argument. This transformation of \(\left\| {\textbf{R}}(t) \right\| \) is detailed below.
By product rule, the total time derivative of the first summand in (45) yields
where \({\textbf{D}}= {\textbf{I}}_{n \times n} \otimes {\mathop {\textrm{diag}}}(i N_{{\textbf{u}}}\omega t, \dots , -i N_{{\textbf{u}}}\omega t)\) (cf. (40)) is the matrix that satisfies \({\dot{{\textbf{C}}}} = {\textbf{C}}{\textbf{D}}\) and \({\dot{{\textbf{Q}}}} = {\textbf{A}}{\textbf{Q}}\) follows from its definition. Below, the dependency on t in the matrices is omitted for the sake of brevity. Substitution of \({\textbf{Q}}\), \({\textbf{L}}\) into (45) yields
To exploit the diagonal structure (38) of \({\textbf{C}}\), the matrices \({\textbf{Q}}, {\textbf{L}}\in \mathbb {C}^{n (2 N_{\textbf{u}}+ 1) \times (2 N_{\textbf{u}}+ 1)}\) are segmented into stacks of column vectors of length \(2N_{{\textbf{u}}} + 1\) via
and \({\textbf{Q}}\) analogously. For the first summand in (49), this gives
where each of the indicated entries is a time-dependent scalar in \(\mathbb {C}\). Similarly, the second summand can be separated into its entries to yield
The still time-dependent \({\textbf{c}}_l(t)\) is generated from the constant coefficients \({\hat{{\textbf{c}}}}_l\) via the diagonal matrix \({\textbf{V}}(t)\) as in (40). Collecting all unknown coefficients into one large vector \({\hat{{\textbf{c}}}}_\textrm{all}\), the (i, j)-th scalar entry of the matrices in (49) can be expressed by
In (53a), only the i-th block is nonzero.
If the Frobenius norm is used for the residual, all absolute squared values of the entries of the matrix (49) are summed, and this gives the expression
Finally, noting that \({\hat{{\textbf{c}}}}_{\textrm{all}}\) is not time-dependent, it can be pulled outside the integral to yield the quadratic cost function (47) with
Therefore, the search for the best choice for the projection matrix \({\textbf{C}}_{\textrm{var}}\) can be formulated as a quadratic program
where the equality constraint encodes the normalization condition (41a). The condition (41b) is not explicitly stated in the quadratic program. This is because minimizers of (56) always fulfill this condition. From an arbitrary candidate \({\hat{{\textbf{c}}}}_{\textrm{all}}\), one can construct a symmetric candidate \({\hat{{\textbf{c}}}}_{\textrm{sym}}\) which fulfills (41b) and for which \({\textbf{R}}\) has the same real part and zero imaginary part, meaning that \(\left\| {\textbf{R}} \right\| ^2\) can not be larger for the symmetric candidate than for the non-symmetric one. The proof of this is sketched in Appendix B.3.
As the matrix \({\varvec{\Theta }}(t)\) is of size \({n(2N_{{\textbf{u}}} \!+\! 1) \!\times } {n(2 N_{{\textbf{u}}} \!+\! 1)}\), and therefore rather large, efficient numerical determination of the integral (56a) is crucial to retain a numerically efficient stability method. Because the time-dependency of \({\varvec{\Theta }}\) is introduced by terms of the form \(\text {e}^{i k \omega t}\), the integral can be reformulated into a (infinite) sum of inner products with Fourier base functions if the power series expression for the matrix exponential is used. This suggests that the integral could be computed efficiently using FFT methods. However, due to the matrix exponential there is no limit in frequency of these terms and aliasing effects must be considered.
Alternatively, the integral can be determined using numerical quadrature schemes. This is accurate, but computationally expensive. Finally, it is also an option to require the integrand to be zero only at specific time instants. This reduces the quadratic program to a linear equation system. While this approach does not minimize the quadratic program (56) in an integral sense, the resulting approximate monodromy matrix seems to be relatively accurate in application.
5 Numerical examples
The theoretical results of the previous sections will be illustrated in this section using some numerical examples, which will allow us to demonstrate the numerical efficiency and accuracy of the proposed projection-based Hill method. The Mathieu equation is utilized as a simple linear time-periodic system of the form (14) to explicitly illustrate the Koopman lift and the projection-based stability approach. To demonstrate the computational advantage for larger numerical orders, the linearization of the vertically excited n-pendulum is then considered as a generalization of the Mathieu equation with arbitrary degrees of freedom.
5.1 Mathieu equation
The Mathieu equation
is an example of a Hill differential equation [47], which has become very well-known since it results from linearization of a number of applications, among them rolling of container ships [48] and a vertically excited pendulum [49]. After bringing the system into first-order-form
with \({\textbf{x}}= [x, {\dot{x}}]^{\mathop {\textrm{T}}}\), (58) is a linear periodic time-varying homogeneous system of the form (12) with system period \({\tilde{T}} = \frac{\pi }{\omega }\), meaning that it is suitable to explore the stability methods of Sect. 4. Necessarily, the system is also T-periodic with \(T = 2{\tilde{T}} = \frac{2\pi }{\omega }\). It is known that the only parameter combinations of (58) which admit non-trivial T-periodic solutions are located at the stability boundaries [39, 50]. The stability boundaries of the Mathieu equation can therefore be identified using the HBM or the shooting method. Below, the base frequency \(\omega \) (i.e., including the first subharmonics of the system) has been chosen for investigation using the frequency-based methods. This is due to two reasons: First, as the stability boundaries may admit T-periodic or \(\frac{T}{2}\)-periodic solutions, this choice allows to identify all stability boundaries using one unified HBM approach without further distinction. Second, in the projection-based Hill method, this choice of base frequency allows to better showcase the influence of the projection matrix.
The equivalence of the Koopman lift matrices, the Hill matrix and the HBM are explicitly verified for the smallest possible frequency order \(N_{{\textbf{u}}} = 1\). First, the Hill matrix is constructed in the standard way. The Fourier decomposition of \({\textbf{J}}(t)\) can be read directly from (58). The nonzero Fourier coefficients with base frequency \(\omega \) are
and all others vanish. By construction using (18), the Hill matrix of frequency order 1 reads
The block-Toeplitz-like structure with additional diagonal elements is visible in (61). Furthermore, it is obvious through the parameter b that terms of harmonic 2 influence the Hill matrix, even if the frequency order was chosen to be \(N_{{\textbf{u}}} = 1 < 2\).
Further, assume there exists a (potentially non-trivial) periodic solution \({\textbf{x}}_p =\sum _{j} {\textbf{p}}_j \text {e}^{i j \omega t}\). Because the original dynamics (58) is already linear, this also holds for the perturbed dynamics
With (62) expressed explicitly in Fourier series form
the explicit determination of the time derivatives of the Koopman basis functions (26) for the perturbed dynamics yields with the index shift \({{\tilde{j}} = j + k}\)
for the first state and
for the second state. The coefficients for the basis functions can be identified in (64) by inspection. For the state-dependent basis functions with \({N_{{\textbf{u}}} = 1}\), this yields
The blocks of \({\textbf{A}}\) have been visually separated to indicate the dependence on the individual states. The selection matrix
necessary to reorder the basis \({\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}\) as required by Theorem 3 can be determined by inspection. With this, it is indeed easy to verify that \({\textbf{H}}= {\textbf{U}}{\textbf{A}}{\textbf{U}}^{\mathop {\textrm{T}}}\) holds for Eqs. (61), (65), (66).
The state-independent terms in (64) can be collected into the \({\textbf{B}}\) matrix. For the considered case \(N_{{\textbf{u}}} = 1\), only the values \(k, j \in \left\{ -1, 0, 1\right\} \) are considered. As expected from Theorem 2, this yields two stacked Toeplitz matrices \({{\textbf{B}}^{\mathop {\textrm{T}}}= [{\textbf{B}}_1^{\mathop {\textrm{T}}}, {\textbf{B}}_2^{\mathop {\textrm{T}}}]}\) with
and \({\textbf{B}}_2\) omitted for the sake of brevity. The expected Toeplitz structure and the HBM equations up to order \(2 N_{{\textbf{u}}}\) are clearly visible. It is also easy to see that \({\textbf{B}}_1\) holds the HBM equations up to order 2 for the first (time-independent) row of (58).
The accuracy of a stability traverse is investigated in Fig. 3 for the Mathieu equation with \(\omega = 1\) and \(b = 1.21\). The parameter a takes the values \(-0.367\) and \(-0.3673\), respectively. Between these values, a stability change from unstable to stable occurs, where the pair of Floquet multipliers meet at 1, and continue on the unit circle as a complex conjugated pair. The Floquet multipliers labeled as true in Fig. 3 were determined using the time-integration method with a high relative and absolute tolerance of \(10^{-14}\) each. In contrast, all Hill-matrix-based methods rely on a Hill matrix of relatively low frequency order \(N_{{\textbf{u}}} = 4\), such that the differences in performance are more visible.
From the figures, it is apparent that the projection-based method with an optimized projection matrix \({\textbf{C}}_{\textrm{var}}\) (i.e., by solving (56)) can be able to track the true Floquet multipliers more closely than any Floquet multiplier candidates obtained directly from the eigenvalues of the Hill matrix allow. Even more, both considered sorting methods choose another pair of eigenvalues than the closest one.
The stability regions of the Mathieu equation are often visualized in a so-called Ince–Strutt diagram [51]. Figure 4 showcases the properties of the different approaches for drawing this stability map using the Hill matrix of a relatively low frequency order \(N_{{\textbf{u}}} = 4\). The color indicates the absolute value of the largest Floquet multiplier (in magnitude). Dark blue colors indicate a maximum value of exactly 1, i.e., stable regions. White color indicates a maximum value larger than 1, i.e., unstable regions.
For Hill equations, it is known that the product of both Floquet multipliers must always equal to 1 [39], i.e., the largest Floquet multiplier may never admit an absolute value smaller than one. In the diagrams, red and purple regions correspond to parameter combinations where the largest identified Floquet multiplier has an absolute value smaller than one, meaning that the identified Floquet multipliers can certainly not be the true ones. In every figure, the true stability boundaries are given in green by the solution of an accurate shooting method.
If all eigenvalues of the Hill matrix are considered for stability (naive approach, Fig. 4a), there are large regions that are wrongly classified as unstable, while none of the unstable regions are wrongly classified as stable. This is expected since in the unstable case, the best approximations will always be among the considered eigenvalues, but in the stable case the additional candidates add additional possibilities of asserted instability. In contrast, the classical Hill method with sorting procedures, which is the current state-of-the-art, classifies most of the stable regions correctly. This is visualized in Fig. 4b for the imaginary-part-based criterion [23, 30] and in Fig. 4c for the symmetry-based criterion [27, 28]. However, in the instability tongue that is separated by non-trivial solutions of period T, red artifacts that are classified as stable are visible in both approaches. These correspond to cases where the sorting algorithm did not choose the correct Floquet multipliers (of which one would be stable, i.e., real-valued and \(<1\), and the other unstable, i.e., real-valued and \(> 1\)), but rather chose two instances of the stable class, both with real parts \(< 1\). With the naive projection matrix, the novel projection-based approach preserves most of the stability regions, while not exhibiting any stable artifacts. However, at the edges of the stable regions, in particular around \(a = 0.5\) and \(b = 1\), slightly larger values of the magnitude are visible. The stable regions are slightly underestimated. A very similar behavior can also be observed with the optimized projection matrix \({\textbf{C}}_{\textrm{var}}\). The example with the naive projection matrix shows that the presented method can be very accurate, even in its simplest form which is easy to implement since only the matrix equation (4.1) is needed.
5.2 Vertically excited multiple pendulum
The Mathieu equation considered in Sect. 5.1 can result from linearization of a vertically excited mathematical pendulum, also called the Kapitza pendulum [52]. As a scalable generalization for arbitrary degrees of freedom, the linearized dynamics of a vertically excited multiple pendulum is considered. A sketch of the considered mechanical system is given in Fig. 5. The pendulum consists of \({n_{\textrm{p}}}\) joints, each of mass m, with viscous absolute damping \({\hat{d}}\), linked by \({n_{\textrm{p}}}\) rods of length l. The minimal coordinates \({\varvec{\theta }= \left( \theta _1, \dots , \theta _{{n_{\textrm{p}}}}\right) ^{\mathop {\textrm{T}}}}\) are the absolute angles of the individual joints. The suspension point of the pendulum moves vertically with \(y_0(t) = {\hat{y}}_0 \cos (2\omega t)\). Gravitation acts in the vertical direction.
The equations of motion for the vertically excited pendulum can be derived similar to [53]. We define the auxiliary vectors
as well as matrices \(\mathcal {S}(\varvec{\theta }), \mathcal {C}(\varvec{\theta }) \in \mathbb {R}^{{n_{\textrm{p}}}\times {n_{\textrm{p}}}}\) with
Dropping the arguments for the sake of brevity, the potential energy \(V(\varvec{\theta }, t)\) and the kinetic energy \(T(\varvec{\theta }, {\dot{\varvec{\theta }}}, t)\) are given by
Using the Lagrange equations of the second kind (see, e.g., [54, p. 76]), the equations of motion are given by
after some algebra. Introducing the abbreviations
and linearizing around the origin, the first-order linearized dynamics of the vertically excited pendulum is
which, after inversion of the left matrix, is of the form \({\dot{{\textbf{y}}}} = {\textbf{J}}(t) {\textbf{y}}\) that can be analyzed using the presented methods. The total number of system states is \(n = 2{n_{\textrm{p}}}\). The relation between the classical Mathieu equation (58) and the linearized vertically excited multiple pendulum is visible from (72). The total number n of states as considered throughout this paper is \(n = 2{n_{\textrm{p}}}\).
To analyze the convergence behavior of our proposed method, the accuracy of the Floquet multipliers of the equilibrium for one specific parameter set (a, b, d) is evaluated for various truncation orders \(N_{{\textbf{u}}}\) and using the various approaches discussed in this paper. As a basis for comparison, the “true” Floquet multipliers are determined by integrating the variational equation (14) using the MATLAB function ode45 with absolute and relative tolerances of \(10^{-13}\). The total Floquet multiplier error is defined as the square root of the sum of the squared absolute differences between the true Floquet multipliers and the obtained Floquet multipliers, while the latter are ordered such that this error is minimal. More formally, let \(\mathcal {P}:= \left\{ \pi : \left\{ 1, \dots , n\right\} \rightarrow \left\{ 1, \dots , n\right\} \vert \pi \text {~bijective} \right\} \) be the (finite) set of permutations, i.e., reorderings, of the index set \(\left\{ 1, \dots , n\right\} \). Then, the total Floquet multiplier error is given by
For the two standard Hill approaches, the eigenvalues and eigenvectors of the Hill matrix \({\textbf{H}}\) were determined using the MATLAB procedure eig. The sorting procedure based on the imaginary part as described in [23, 26, 30] then singles out the n eigenvalues with least imaginary part in modulus, while the symmetry-based sorting procedure singles out the n eigenvalues whose eigenvectors have lowest weighted mean according to [27]. The Floquet multipliers are then determined from the Floquet exponents (i.e., the identified eigenvalues) using (15). The corresponding errors are depicted in Fig. 6 in dashed blue and dotted red for the imaginary part criterion and the symmetry criterion, respectively.
The presented novel Koopman-based method is evaluated for two choices of the projection matrix \({\textbf{C}}\) (see Sect. 4.3). The Floquet multipliers are determined as the eigenvalues of the approximate monodromy matrix (35). The matrix exponential in (35) is evaluated directly with its action onto the matrix \({\textbf{W}}\) using the MATLAB function exmpv [46, 55]. The dash-dotted yellow line shows the accuracy of the Floquet multipliers obtained from the monodromy approximation using the naive projection choice \({\textbf{C}}_0\) (31), while the solid purple line indicates the accuracy obtained by a more informed projection matrix
which was obtained by inspection after running the optimization (56) for a few test cases. From the figure, it is visible that all considered approaches eventually converge to the true Floquet multipliers. The final error of order \(10^{-12}\) can be attributed to inaccuracies of the numerical integration. The imaginary-part-based criterion, while being the only one with a rigorous convergence proof for \(n \rightarrow \infty \), performs highly inaccurate for smaller \(N_{{\textbf{u}}}\). Moreover, the choice of projection matrix significantly influences the performance of the novel projection-based approach. While the naive choice of projection matrix does converge toward the correct value, the optimization-based projection matrix exhibits a significantly better convergence rate which can compete with the symmetry-based criterion or outperforms it.
The data set of Fig. 6 is again plotted in Fig. 7, but against the computation time instead of the frequency order, giving a work-precision diagram. The strength of the projection-based methods for higher frequency orders is apparent in this figure. While convergence of the imaginary-part-based method with respect to the frequency order \(N_{{\textbf{u}}}\) is better than that of the new projection-based method for the naive projection choice \({\textbf{C}}_0\), the accuracy of the projection-based method is higher than that of the imaginary-part-based method for any computation time. The reason for this is that the eigenproblem becomes more expensive than the matrix exponential for higher matrix dimensions, i.e., for higher \(N_{{\textbf{u}}}\). The same property can also be observed regarding the symmetry-based approach and the novel projection-based approach with optimized projection matrix \({\textbf{C}}_1\). The projection-based approach is able to achieve maximum accuracy already at approx. \(0.1\textrm{s}\) compared to approx. \(0.25\textrm{s}\) for the symmetry-based approach. This is a ratio of \(\frac{2}{5}\), which is considerably lower than the corresponding ratio \(\frac{15}{18}\) of frequency orders. If the system dimension increases, this efficiency difference increases as well as the size \(n(2N_{{\textbf{u}}}+1)\times n(2N_{{\textbf{u}}}+1)\) of the Hill matrix is influenced by a product of n and \(N_{{\textbf{u}}}\). Therefore, the superior efficiency of the projection-based approaches against the standard approaches is even more prominent. Figure 8 again compares computation time against accuracy for the various approaches, but for a pendulum with 15 instead of 6 links. Since the number of states is increased, the computation time for all the considered approaches is larger than in Fig. 7. However, the increase in number of states impacts the standard Hill methods which rely on solving the large eigenvalue problem more than the projection-based method. This is because of the key feature of the new method: a moderate growth of computational cost as sparsity can be exploited in the action of the matrix exponential. In fact, in Fig. 8, the break-even point between the symmetry-based method and the projection-based method with the optimized projection matrix already occurs at \({N_{{\textbf{u}}} = 6}\). The imaginary-part-based Hill method fails to converge within the depicted computation time interval.
6 Conclusions
In this paper, a relationship between the HBM, the Hill method and the Koopman lift with specific basis functions has been addressed. It has been shown that the Hill matrix is the system matrix of a linear time-invariant dynamical system of higher order which approximates the perturbed dynamics. This relationship has been used to derive a novel stability method based on projecting the Hill matrix down to original system size, instead of computing all its eigenvalues.
The resulting stability criterion in its naive form is remarkably simple to implement. It only needs a matrix exponential and two projection matrices, which are the same for all systems and easy to construct (see (31), (33)). It has been shown in the examples of Sect. 5 that this simple method can compete with the state-of-the-art algorithms in terms of Floquet multiplier accuracy over computational effort.
To further improve the accuracy of the proposed method, an optimization-based approach for the choice of the projection matrix through a quadratic program has been presented in Sect. 4.3. While the determination of the matrix integral in (56) is more computationally expensive, it has been shown in Sect. 5 that this optimized projection matrix allows for even better accuracy.
There are many topics for further research expanding from the results of this work: The approach itself offers opportunities for additional development both in its theoretical as well as for its computational properties. Further, there are many possible interesting applications of the approach to technical systems, and extensions to wider classes of systems would be valuable.
With respect to theoretical properties, there is currently no rigorous convergence proof for the novel approach for any choice of projection matrix. Such a convergence proof would aid in an a priori determination which method to employ for the best results.
Considering computational properties, while the presented approach does reduce computational effort compared to the state-of-the-art approaches, some bottlenecks remain. In particular, the efficient sparsity-promoting determination of the matrix exponential with projection from both sides as well as the integral in the optimization problem (56) would benefit from more efficient computation techniques. As the latter is constructed by products of the Fourier coefficients of \({\textbf{J}}\) in \({\textbf{A}}\) and additional Fourier terms, there could exist an operation to obtain this integral directly from the (FFT) Fourier series of \({\textbf{J}}(t)\).
From an application point of view, going beyond the simple and mainly academical examples presented in this work, it would also be expedient to apply the novel stability method to systems of more practical relevance. To achieve this goal, it would be beneficial to integrate the novel method within an established continuation framework. The authors believe that the MANLAB continuation framework [25, 28] would be especially suitable because the Hill matrix can be constructed in this framework without much additional effort. Large systems that were already analyzed extensively using the MANLAB framework (e.g., [56]) could benefit from the stability insights of our proposed method, while simultaneously serving as practical examples of the performance of the method.
Regarding possible extensions, while some relations were established in Theorem 1 for polynomial basis functions of the Koopman lift, most sections of this work rely on basis functions that are linear in the state. Some recent results [57, 58] make statements about return time and period for autonomous systems based on the Carleman linearization. As our (full) basis provides a natural extension of the Carleman linearization, these results could possibly be integrated into the presented framework.
Finally, it would be of practical value to extend the method to a wider class of systems, for example, possibly including delay differential equations (DDEs) with delayed coordinates in the basis functions.
Data availability
All numerical data in this work have been generated from the considered system Eqs. (58), (72), with the approaches described in this work and the cited works, using MATLAB standard methods and the MATLAB function expmv [55]. Therefore, it is possible to completely reproduce the data from the information given in this work, except for the computation times in the work-precision diagrams. These computation times have been evaluated on a Windows PC, and more detailed computation time data can be obtained from the authors upon request.
References
Mauroy, A., Mezić, I., Susuki, Y. (eds.): The Koopman Operator in Systems and Control: Concepts, Methodologies and Applications. Lecture Notes in Control and Information Sciences, vol. 484. Springer, Cham (2020)
Brunton, S.L., Budišić, M., Kaiser, E., Kutz, J.N.: Modern Koopman theory for dynamical systems. SIAM Rev. 64(2), 229–340 (2022). https://doi.org/10.1137/21m1401243
Williams, M.O., Kevrekidis, I.G., Rowley, C.W.: A data-driven approximation of the Koopman operator: extending dynamic mode decomposition. J. Nonlinear Sci. 25(6), 1307–1346 (2015). https://doi.org/10.1007/s00332-015-9258-5
Kono, Y., Susuki, Y., Hikihara, T.: Modeling of advective heat transfer in a practical building atrium via Koopman mode decomposition. In: Mauroy, A., Mezić, I., Susuki, Y. (eds.) The Koopman Operator in Systems and Control: Concepts, Methodologies, and Applications, pp. 481–506. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-35713-9_18
Korda, M., Mezić, I.: Koopman model predictive control of nonlinear dynamical systems. In: Mauroy, A., Mezić, I., Susuki, Y. (eds.) The Koopman Operator in Systems and Control: Concepts, Methodologies and Applications, pp. 235–255. Springer, Cham (2020)
Koopman, B.O.: Hamiltonian systems and transformation in Hilbert space. Proc. Natl. Acad. Sci. USA 17(16577368), 315–318 (1931). https://doi.org/10.1073/pnas.17.5.315
Mezić, I.: Spectral properties of dynamical systems, model reduction and decompositions. Nonlinear Dyn. 41(1), 309–325 (2005). https://doi.org/10.1007/s11071-005-2824-x
Mauroy, A., Mezić, I., Moehlis, J.: Isostables, isochrons, and Koopman spectrum for the action-angle representation of stable fixed point dynamics. Physica D 261, 19–30 (2013). https://doi.org/10.1016/j.physd.2013.06.004
Mohr, R., Mezić, I.: Construction of eigenfunctions for scalar-type operators via Laplace averages with connections to the Koopman operator (2014). https://doi.org/10.48550/arXiv.1403.6559
Mauroy, A., Susuki, Y., Mezić, I.: Introduction to the Koopman operator in dynamical systems and control theory. In: Mauroy, A., Susuki, Y., Mezić, I. (eds.) The Koopman Operator in Systems and Control: Concepts, Methodologies and Applications, pp. 3–33. Springer, Cham (2020)
Nayfeh, A.H., Mook, D.T., Holmes, P.: Nonlinear oscillations. J. Appl. Mech. 47(3), 692–692 (1980). https://doi.org/10.1115/1.3153771
Bentvelsen, B., Lazarus, A.: Modal and stability analysis of structures in periodic elastic states: application to the Ziegler column. Nonlinear Dyn. 91(2), 1349–1370 (2018). https://doi.org/10.1007/s11071-017-3949-4
Karkar, S., Vergez, C., Cochelin, B.: Oscillation threshold of a clarinet model: a numerical continuation approach. J. Acoust. Soc. Am. 131(1), 698–707 (2012). https://doi.org/10.1121/1.3651231
Noiray, N., Durox, D., Schuller, T., Candel, S.: A unified framework for nonlinear combustion instability analysis based on the flame describing function. J. Fluid Mech. 615, 139–167 (2008). https://doi.org/10.1017/S0022112008003613
da Cruz Scarabello, M., Messias, M.: Bifurcations leading to nonlinear oscillations in a 3D piecewise linear memristor oscillator. Int. J. Bifurc. Chaos 24(01), 1430001 (2014). https://doi.org/10.1142/s0218127414300018
Cheffer, A., Savi, M.A., Pereira, T.L., de Paula, A.S.: Heart rhythm analysis using a nonlinear dynamics perspective. Appl. Math. Model. 96, 152–176 (2021). https://doi.org/10.1016/j.apm.2021.03.014
Peeters, M., Viguié, R., Sérandour, G., Kerschen, G., Golinval, J.-C.: Nonlinear normal modes, Part II: toward a practical computation using numerical continuation techniques. Mech. Syst. Signal Process. 23(1), 195–216 (2009). https://doi.org/10.1016/j.ymssp.2008.04.003
Kevrekidis, I.G., Aris, R., Schmidt, L.D., Pelikan, S.: Numerical computation of invariant circles of maps. Physica D 16(2), 243–251 (1985). https://doi.org/10.1016/0167-2789(85)90061-2
Parker, T.S., Chua, L.O.: Practical Numerical Algorithms for Chaotic Systems. Springer, Berlin (1989)
Morrison, D.D., Riley, J.D., Zancanaro, J.F.: Multiple shooting method for two-point boundary value problems. Commun. ACM 5(12), 613–614 (1962). https://doi.org/10.1145/355580.369128
Ascher, U.M., Mattheij, R.M.M., Russell, R.D.: Numerical Solution of Boundary Value Problems for Ordinary Differential Equations. Soc. Ind. Appl. Math. (1995). https://doi.org/10.1137/1.9781611971231
Krack, M., Gross, J.: Harmonic Balance for Nonlinear Vibration Problems. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-14023-6
Detroux, T., Renson, L., Masset, L., Kerschen, G.: The harmonic balance method for bifurcation analysis of large-scale nonlinear mechanical systems. Comput. Methods Appl. Mech. Eng. 296, 18–38 (2015). https://doi.org/10.1016/j.cma.2015.07.017
Cameron, T.M., Griffin, J.H.: An alternating frequency/time domain method for calculating the steady-state response of nonlinear dynamic systems. J. Appl. Mech. 56(1), 149–154 (1989). https://doi.org/10.1115/1.3176036
Cochelin, B., Vergez, C.: A high order purely frequency-based harmonic balance formulation for continuation of periodic solutions. J. Sound Vib. 324(1–2), 243–262 (2009). https://doi.org/10.1016/j.jsv.2009.01.054
Zhou, J., Hagiwara, T., Araki, M.: Spectral characteristics and eigenvalues computation of the harmonic state operators in continuous-time periodic systems. Syst. Control Lett. 53(2), 141–155 (2004). https://doi.org/10.1016/j.sysconle.2004.03.002
Guillot, L., Lazarus, A., Thomas, O., Vergez, C., Cochelin, B.: A purely frequency based Floquet–Hill formulation for the efficient stability computation of periodic solutions of ordinary differential systems. J. Comput. Phys. 416, 109477 (2020). https://doi.org/10.1016/j.jcp.2020.109477
Lazarus, A., Thomas, O.: A harmonic-based method for computing the stability of periodic solutions of dynamical systems. Comptes Rendus Mécanique 338(9), 510–517 (2010). https://doi.org/10.1016/j.crme.2010.07.020
Peletan, L., Baguet, S., Torkhani, M., Jacquet-Richardet, G.: A comparison of stability computational methods for periodic solution of nonlinear problems with application to rotordynamics. Nonlinear Dyn. 72(3), 671–682 (2013). https://doi.org/10.1007/s11071-012-0744-0
Moore, G.: Floquet theory as a computational tool. SIAM J. Numer. Anal. 42(6), 2522–2568 (2005). https://doi.org/10.1137/s0036142903434175
Wu, J., Hong, L., Jiang, J.: A robust and efficient stability analysis of periodic solutions based on harmonic balance method and Floquet–Hill formulation. Mech. Syst. Signal Process. 173, 109057 (2022). https://doi.org/10.1016/j.ymssp.2022.109057
Bayer, F., Leine, R.I.: A Koopman view on the harmonic balance and Hill method. In: Proceedings of the 10th European Nonlinear Dynamics Conference (2022). https://enoc2020.sciencesconf.org/394116
Naylor, A.W., Sell, G.R.: Linear Operator Theory in Engineering and Science. Holt, Rinehart & Winston, New York (1971)
Budišić, M., Mohr, R., Mezić, I.: Applied Koopmanism. Chaos: Interdiscip. J. Nonlinear Sci. 22(4), 047510 (2012). https://doi.org/10.1063/1.4772195
Carleman, T.: Application de la théorie des équations intégrales linéaires aux systèmes d’équations différentielles non linéaires. Acta Math. 59, 63–87 (1932)
Berrueta, T.A., Abraham, I., Murphey, T.: Experimental applications of the Koopman operator in active learning for control. In: Mauroy, A., Mezić, I., Susuki, Y. (eds.) The Koopman Operator in Systems and Control, pp. 421–450. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-35713-9_16
Champion, K.P., Brunton, S.L., Kutz, J.N.: Discovery of nonlinear multiscale systems: sampling strategies and embeddings. SIAM J. Appl. Dyn. Syst. 18(1), 312–333 (2019). https://doi.org/10.1137/18m1188227
Bittanti, S., Colaneri, P.: Invariant representations of discrete-time periodic systems. Automatica 36(12), 1777–1793 (2000). https://doi.org/10.1016/S0005-1098(00)00087-X
Teschl, G.: Ordinary Differential Equations and Dynamical Systems. Graduate Studies in Mathematics, vol. 140. American Mathematical Society, Providence, Rhode Island (2012)
Von Groll, G., Ewins, D.J.: The harmonic balance method with arc-length continuation in rotor/stator contact problems. J. Sound Vib. 241(2), 223–233 (2001). https://doi.org/10.1006/jsvi.2000.3298
Golub, G.H.V., Van Loan, C.F.V.: Matrix Computations. North Oxford Academic, Oxford (1986)
Bruder, D., Fu, X., Gillespie, R.B., Remy, C.D., Vasudevan, R.: Data-driven control of soft robots using Koopman operator theory. IEEE Trans. Rob. 37(3), 948–961 (2021). https://doi.org/10.1109/TRO.2020.3038693
Johnson, C.A., Balakrishnan, S., Yeung, E.: Heterogeneous mixtures of dictionary functions to approximate subspace invariance in Koopman operators (2022). https://doi.org/10.48550/arXiv.2206.13585
Korda, M., Mezić, I.: Linear predictors for nonlinear dynamical systems: Koopman operator meets model predictive control. Automatica 93, 149–160 (2018). https://doi.org/10.1016/j.automatica.2018.03.046
Moler, C., Van Loan, C.: Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later. SIAM Rev. 45(1), 3–49 (2003). https://doi.org/10.1137/S00361445024180
Al-Mohy, A.H., Higham, N.J.: Computing the action of the matrix exponential, with an application to exponential integrators. SIAM J. Sci. Comput. 33(2), 488–511 (2011). https://doi.org/10.1137/100788860
Magnus, W., Winkler, S.: Hill’s Equation. Interscience Publishers, New York (1966)
Moideen, H., Falzarano, J., Somayajula, A.: Parametric roll of container ships in head waves. Ocean Systems Engineering 2: 239–255. (2012). https://doi.org/10.12989/ose.2012.2.4.239
Leine, R.I.: Non-smooth stability analysis of the parametrically excited impact oscillator. Int. J. Non-Linear Mech. 47(9), 1020–1032 (2012). https://doi.org/10.1016/j.ijnonlinmec.2012.06.010
Kovacic, I., Rand, R., Mohamed Sah, S.: Mathieu’s equation and its generalizations: overview of stability charts and their features. Appl. Mech. Rev. 70(2) (2018). https://doi.org/10.1115/1.4039144
Abboud, E., Thomas, O., Grolet, A., Mahé, H.: On the solution of the Mathieu equation with multiple harmonic stiffness, parametric amplification for constant and harmonic forcing. In: Proceedings of the 10th European Nonlinear Dynamics Conference (2022). https://enoc2020.sciencesconf.org/341631
Bartuccelli, M.V., Gentile, G., Georgiou, K.V.: On the stability of the upside-down pendulum with damping. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 458(2018), 255–269 (2001). https://doi.org/10.1098/rspa.2001.0859
Schiele, K., Hemmecke, R.: Migration effects in driven multiple pendula. Z. Angew. Math. Mech. 81(5), 291–303 (2001)
Meirovich, L.: Methods of Analytical Dynamics. Advanced Engineering Series, vol. 3. McGraw-Hill Book Company, New York (1970)
Higham, N.: Matrix exponential times a vector. MATLAB Central File exchange (2022). www.mathworks.com/matlabcentral/fileexchange/29576-matrix-exponential-times-a-vector
Debeurre, M., Grolet, A., Mattei, P.-O., Cochelin, B., Thomas, O.: Nonlinear modes of cantilever beams at extreme amplitudes: numerical computation and experiments. In: Brake, M.R.W., Renson, L., Kuether, R.J., Tiso, P. (eds.) Nonlinear Struct. Syst., vol. 1, pp. 245–248. Springer, Cham (2023)
Hubay, C.Á., Kalmár-Nagy, T.: Return time approximation in planar nonlinear systems. J. Sound Vib. 508, 116200 (2021). https://doi.org/10.1016/j.jsv.2021.116200
Hubay, C.Á., Kalmár-Nagy, T.: Period approximation for nonlinear oscillators with Carleman linearization. In: Proceedings of the 10th European Nonlinear Dynamics Conference (2022). https://enoc2020.sciencesconf.org/309588
Reed, M., Simon, B.: Functional Analysis. Methods of Modern Mathematical Physics, vol. 1, p. 400. Academic Press, San Diego (1980)
Ehrenfest, P., Kamerlingh Onnes, H.: XXXIII. Simplified deduction of the formula from the theory of combinations which Planck uses as the basis of his radiation theory. Lond Edinb Dublin Philos Mag J Sci 29(170), 297–301 (1915). https://doi.org/10.1080/14786440208635308
Funding
Open Access funding enabled and organized by Projekt DEAL. The authors declare that no funds, grants, or other support was received during the preparation of this manuscript.
Author information
Authors and Affiliations
Contributions
Both authors contributed to the conceptualization, design and methodology. The formal analysis was performed by Fabia Bayer. The original draft of the manuscript was prepared by Fabia Bayer and both authors commented on previous versions of the manuscript. Remco Leine was responsible for funding acquisition and supervision. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Multi-index calculation rules
For convenience, the standard multi-index calculation rules (see, for example, [59, p. 319]) are revisited. A multi-index is a tuple \(\varvec{\beta }\in \mathbb {N}_0^d\) with nonnegative integer entries. In particular, a multi-index \(\varvec{\beta }= (\beta _1, \dots , \beta _d)\) has the 1-norm
and a factorial
given by the product of the factorials of all its components. For a vector \({\textbf{x}}\in \mathbb {C}^{d}\), exponentiation is given by
and for a function \(f: \mathbb {R}^d \rightarrow \mathbb {C}\), the \(\varvec{\beta }\)-th derivative is given by
It is known in combinatorics that the number of multi-indices \(\varvec{\beta }\in \mathbb {N}_0^d\) with \( \left\| \varvec{\beta } \right\| \le N\) is given by \(\left( {\begin{array}{c}N + d\\ d\end{array}}\right) \) [60]. This is also the number of unique monomials of the form (A3) with degree \(\le N\), including \({\textbf{x}}^\textbf{0}\).
Appendix B: Proofs for the theorems
In this section, the theorems of Sect. 3.2 are proven formally. The slightly unusual matrix-valued inner product notation (1)–(2c) is heavily utilized throughout the proofs for the sake of brevity.
1.1 B.1 Theorems 1 and 2
Theorem 2 will be proven first, and Theorem 1 will result as a consequence from that proof. Recall Theorem 2:
Theorem 2
Let \({\dot{{\textbf{z}}}} = {\textbf{A}}({\textbf{p}}) {\textbf{z}}+ {\textbf{B}}({\textbf{p}}) {\textbf{u}}\) be the lifted dynamics of system (6) with linear basis functions \({\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}\) of frequency order \(N_{{\textbf{u}}}\) that are sorted as in (22), evaluated for the perturbed system around an unknown periodic ansatz of the form (10) up to frequency order at least \(N_{\textrm{HBM}} = 2N_{{\textbf{u}}}\). Then, the matrix \({\textbf{B}}({\textbf{p}}) \in \mathbb {C}^{n (2 N_{{\textbf{u}}} + 1) \times (2 N_{{\textbf{u}}} + 1) }\) consists of n stacked Toeplitz matrices. The l-th Toeplitz matrix \({\textbf{B}}_l\) contains as entries (ignoring duplicates) precisely the \(4N_{{\textbf{u}}}+1\) residuals \(r_{k, l}({\textbf{p}}), \left| k \right| \le 2N_{{\textbf{u}}}\) that follow from the HBM w.r.t the l-th state.
If \({\textbf{B}}({\textbf{p}}) = \textbf{0}\), then all these residuals of the HBM vanish. Conversely, if \({\textbf{p}}\) solves the HBM equations \({{\textbf{r}}_k({\textbf{p}}) = \textbf{0}}, {\left| k \right| \le 2N_{{\textbf{u}}}}\), then it holds that \({\textbf{B}}({\textbf{p}}) = \textbf{0}\).
Proof
For the sake of brevity, bounds of sums are omitted in this proof if they take the values of \(\pm \infty \). Recall that the HBM equations can be expressed as the harmonic residual of the dynamics (29). Let (26) be a linear basis for the Koopman lift as in Theorem 2 with \({\textbf{z}}(t) \approx {\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}({\textbf{y}}(t), t)\). With the ordering (26), the first \(2N_{{\textbf{u}}} + 1\) entries of \({\textbf{z}}\) approximate all basis functions connected to \(y_{1}\), the next \(2 N_{{\textbf{u}}} + 1\) entries approximate all basis functions connected to \(y_2\) et cetera. With this separation, divide the matrix \({{\textbf{B}}({\textbf{p}}) \in \mathbb {C}^{n (2 N_{{\textbf{u}}} + 1) \times (2 N_{{\textbf{u}}} + 1)}}\) into n square matrices \(\left\{ {\textbf{B}}_l\right\} _{l = 1}^n\) such that \({\textbf{B}}_l \in \mathbb {C}^{(2 N_{{\textbf{u}}} + 1) \times (2 N_{{\textbf{u}}} + 1)}\) influences the derivative of \(y_l\). Below, the argument is made for one \({\textbf{B}}_l\) and \({\textbf{B}}\) can be stacked together in the end.
Consider now the time derivative along the system flow of a Koopman basis function corresponding to the l-th state and frequency j, evaluated on the perturbed system:
The inner product \(\left\langle {\dot{\psi }}_{j, l}, {\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}} \right\rangle \) is a row of \({\textbf{A}}\) and \(\left\langle {\dot{\psi }}_{j, l}, {\textbf{u}} \right\rangle \) is a row of \({\textbf{B}}_l\). As the inner product for \({\textbf{A}}\) contains all summands that are dependent on \({\textbf{y}}\) and the inner product for \({\textbf{B}}\) collects all parts that are not dependent on \({\textbf{y}}\), we can set \({\textbf{y}}= \textbf{0}\) in this proof about properties of \({\textbf{B}}\). With this, it results
The inner product with \({\textbf{u}}\) is just a projection onto the Fourier basis functions between \(\pm N_{{\textbf{u}}}\), and therefore, the row of \({\textbf{B}}_l\) that corresponds to frequency j is given by
Comparing two successive rows, i.e., the j-th and the \((j+1)\)-th row of \({{\textbf {B}}}_l\), it is obvious from (B13) that they contain the same entries, but shifted to the right by one element. Adequately, going from row j to row \(j + 1\), the entry \(r_{-N_{{\textbf{u}}} - (j+1), l}\) is added on the left, while the entry \(r_{N_{{\textbf{u}}} - j, l}\) is pushed out on the right. The matrix \({\textbf{B}}_l\) thus has a Toeplitz structure, where all residuals between \(r_{-2N_{{\textbf{u}}}, l}\) (in the bottom left entry of \({\textbf{B}}_l\) with \(j = N_{{\textbf{u}}}\)) and \(r_{2N_{{\textbf{u}}}, l}\) (in the top right entry with \({j = -N_{{\textbf{u}}}}\)) occur, yielding \(4 N_{{\textbf{u}}} + 1\) distinct entries in total.
In particular, if the coefficients \({\textbf{p}}\) describe the HBM solution for order \(2 N_{{\textbf{u}}}\), then all these residuals vanish and it holds that \({\textbf{B}}({\textbf{p}}) = \textbf{0}\). \(\square \)
The arguments of the previous proof can be reused for Theorem 1 with slightly modified assumptions. Recall the theorem:
Theorem 1
Let \({\dot{{\textbf{z}}}} = {\textbf{A}}({\textbf{p}}) {\textbf{z}}+ {\textbf{B}}({\textbf{p}}) {\textbf{u}}\) be the lifted dynamics of frequency order \(N_{\textrm{HBM}}\) of system (6) around an unknown periodic ansatz of the form (10). The \(N_{\textrm{HBM}}\)-th order HBM equations (11), i.e., \({{\textbf{r}}_k \!=\! 0}, \left| k \right| \le N_{\textrm{HBM}}\), are given by \({\textbf{C}}_{{\textbf{z}}} {\textbf{B}}({\textbf{p}}) = \textbf{0}\), where \({\textbf{C}}_{{\textbf{z}}}\) is the constant selection matrix that fulfills \({\textbf{y}}= {\textbf{C}}_{{\textbf{z}}} {\varvec{\Psi }}_{{\textbf{z}}}({\textbf{y}}, t)\) for all t.
Proof
In contrast to the previously proven Theorem 2, in this theorem the basis functions are not restricted to be linear in the state. Due to sesquilinearity of the inner product (2b), however, the selection matrix \({\textbf{C}}_{{\textbf{z}}}\) can be pulled into the expression for \({\textbf{B}}({\textbf{p}})\) via
These expressions can again be evaluated row-wise with (B13) and since \(j = 0\) for all entries of (B14), the condition \({\textbf{C}}_{{\textbf{z}}}{\textbf{B}}({\textbf{p}}) = 0\) is equivalent to \({\textbf{r}}_k = 0\) for all \(\left| k \right| \le N_{\textrm{HBM}}\), which are exactly the HBM equations. \(\square \)
1.2 B.2 Theorem 3
Similarly to the theorems proven previously, it is central in the proof for Theorem 3 to evaluate the inner product explicitly. The theorem is restated for convenience.
Theorem 3
Let \({\dot{{\textbf{z}}}} = {\textbf{A}}({\textbf{p}}) {\textbf{z}}+ {\textbf{B}}({\textbf{p}}) {\textbf{u}}\) be the lifted dynamics around a periodic solution of system (6) with linear basis functions \({\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}\) of frequency order \(N_{{\textbf{u}}}\) that are ordered as in (22). Then, the Hill matrix \({\textbf{H}}\), truncated to frequency order \(N_{{\textbf{u}}}\), for the periodic solution parameterized by \({\textbf{p}}\) results from the matrix \({\textbf{A}}({\textbf{p}})\) by the similarity transform \({\textbf{H}}= {\textbf{U}}{\textbf{A}}({\textbf{p}}) {\textbf{U}}^{\mathop {\textrm{T}}}\), where \({\textbf{U}}\) is an orthogonal permutation matrix that satisfies \({\textbf{U}}{\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}} = ({\textbf{y}}^{\mathop {\textrm{T}}}\ \textrm{e}^{i N_{{\textbf{u}}} \omega t}, \dots , {\textbf{y}}^{\mathop {\textrm{T}}}\ \textrm{e}^{- i N_{{\textbf{u}}} \omega t})^{\mathop {\textrm{T}}}\).
Proof
The matrix \({\textbf{U}}\) is derived from the identity matrix by reordering its rows, and it reorders the entries of \({\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}\) such that the resulting vector has entries descending in frequency, where all states corresponding to the same frequency are collected together. Denote \({\tilde{{\varvec{\Psi }}}}_{{\textbf{z}}}:= {\textbf{U}}{\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}} =: (({\tilde{{\varvec{\Psi }}}}_{{\textbf{z}}})_{-N_{{\textbf{u}}}}^{\mathop {\textrm{T}}}, \dots , ({\tilde{{\varvec{\Psi }}}}_{{\textbf{z}}})_{N_{{\textbf{u}}}}^{\mathop {\textrm{T}}})^{\mathop {\textrm{T}}}\) and separate it into \(2 N_{{\textbf{u}}} + 1\) blocks of length n with \(({\tilde{{\varvec{\Psi }}}}_{{\textbf{z}}})_{k}:= {\textbf{y}}\text {e}^{-i k \omega t}\). First, we show that the Koopman lift performed with basis \({\tilde{{\varvec{\Psi }}}}_{{\textbf{z}}}\) identically yields \({\textbf{H}}\) as its system matrix \({\tilde{{\textbf{A}}}}\), and afterward we demonstrate how performing the lift with \({\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}\) instead of \({\tilde{{\varvec{\Psi }}}}_{{\textbf{z}}}\) demands the additional similarity transform.
As in the proof for Theorem 2, we start by determining the time derivative of the basis functions. For the vector of time derivatives, by the chain rule it holds that
where \({\tilde{{\textbf{f}}}}\) is the nonlinear perturbed dynamics (27a). Evaluating the individual summands of (B17) yields
The terms of order \( \mathcal {O}(\left\| {\textbf{y}} \right\| ^2)\) in (B20) can be dropped because terms of higher polynomial order are not represented in the chosen basis \({\varvec{\Psi }}_{{\textbf{z}}, \textrm{lin}}\). The terms in \({\textbf{b}}(t)\) appear if the candidate ansatz is not a periodic solution. They are purely time-dependent and will remain so after multiplication by (B19). Hence they are collected in the \({\textbf{B}}\) matrix. The column vector in (B18) and the matrix in (B19) can be decomposed into \(2 N_{{\textbf{u}}} + 1\) blocks with n rows and 1 or n columns as indicated above, each block corresponding to a specific frequency. These blocks are labeled in ascending order by k, \(-N_{{\textbf{u}}}\le k \le N_{{\textbf{u}}}\), such that the k-th block corresponds to the term \(\text {e}^{-ik\omega t}\). Equations (B18)–(B20) are substituted into the k-th block in (B17) to yield
where the purely time-dependent terms and the terms of order \( \mathcal {O}(\left\| {\textbf{y}} \right\| ^2)\) have been dropped for the sake of legibility. To obtain the k-th block of the Koopman lift matrix \({\tilde{{\textbf{A}}}}\), the inner product \(\left\langle \left( \dot{{\tilde{{\varvec{\Psi }}}}}_{{\textbf{z}}}\right) _{k}, {\tilde{{\varvec{\Psi }}}}_{{\textbf{z}}} \right\rangle \) is considered. Due to the sesquilinearity of the inner product, both summands in (B23) can be computed separately. It is easy to see that the first summand yields a sparse matrix where only the diagonal in the k-th column block is nonzero. With an index shift
the inner product with the second summand of (B23) yields the matrix
Collecting all row blocks and both summands together, the Koopman lift matrix \({\tilde{{\textbf{A}}}}\) for the re-sorted basis is given by
Comparison of (B26) to the truncated Hill matrix (18) shows the identity \({\tilde{{\textbf{A}}}} = {\textbf{H}}\) for the Koopman lift with the re-sorted basis.
Finally, the similarity transform obtained by the re-ordering is considered. The permutation matrix \({\textbf{U}}\) is constant and can thus be pulled out of the time derivative. With the sesquilinearity of the matrix-valued inner product (2b), (2c), it then follows
where \({\textbf{A}}({\textbf{p}})\) is the Koopman lift with the standard basis. In the last step, it has been exploited that \({\textbf{U}}\) is a real-valued matrix and thus transpose and conjugate transpose coincide. \(\square \)
1.3 B.3 Symmetry properties of the optimization problem
Below, it will be shown that there always exist solutions to the optimization problem (56) fulfilling (41b), even if this constraint is not enforced explicitly. This is summarized in the following proposition.
Proposition 4
For an arbitrary collection \({\hat{{\textbf{c}}}}_{\textrm{all}} \in \mathbb {C}^{n(2 N_{{\textbf{u}}} + 1)}\) of coefficients which admit the residual \({\textbf{R}}\) in the variational equation (45), there exists another collection \({\hat{{\textbf{c}}}}_{\textrm{sym}} \in \mathbb {C}^{n(2 N_{{\textbf{u}}} + 1)}\) constructed by
which fulfills (41b). The residual \({\textbf{R}}_{\textrm{sym}}\) of the variational equation (45) for \({\hat{{\textbf{c}}}}_{\textrm{sym}}\) is real for arbitrary t with \({\textbf{R}}_{\textrm{sym}} = \mathop {\textrm{Re}}({\textbf{R}})\).
The proof for this proposition is only sketched here. Some mathematical steps are only indicated but not performed in detail for the sake of brevity.
Proof
Below, vectors \({\textbf{d}}\in \mathbb {C}^{(2 N_{{\textbf{u}}} + 1)}\) which fulfill (41b) will be called symmetric. The symmetric vectors form a vector space over \(\mathbb {R}\) (but not over \(\mathbb {C}\)).
First, the structure of the Koopman lift matrix \({\textbf{A}}\) is revisited. Applying the similarity transform of Theorem 3 to the Hill matrix explicitly yields for the matrix \({\textbf{A}}\) the structure
Hence, the lj-th block of the matrix \({\textbf{A}}\) contains the Fourier coefficients of the lj-th entry of the system matrix \({\textbf{J}}\). In particular, since \({\textbf{J}}(t)\) admits only real values, \(J_{lj, k} = \overline{J_{lj, -k}}\) and each block \({\textbf{A}}_{lj}\) fulfills a variant of the symmetry property: The \(-k\)-th row is the complex conjugate of the k-th row, with the order of elements reversed. A little algebra shows that for matrices with these properties and symmetric vectors \({\textbf{d}}\in \mathbb {C}^{(2 N_{{\textbf{u}}} + 1)}\), the symmetry is retained though multiplication: \({\textbf{A}}_{lj}{\textbf{d}}\) is symmetric if \({\textbf{d}}\) is symmetric.
If a matrix \({\textbf{P}}= [{\textbf{d}}_{lj}]\) is constructed block-wise from symmetric column vectors \(\left\{ {\textbf{d}}_{lj}\right\} _{l, j = 1}^n\), then the matrix \({\textbf{A}}{\textbf{P}}\) is again constructed from symmetric column vectors since all block entries of \({\textbf{A}}{\textbf{P}}\) can be decoupled into sums of products \({\textbf{A}}_{li} {\textbf{d}}_{ij}\), which each retain the symmetry as described above. In particular, since the matrix \({\textbf{W}}\) in (33) is constructed in the considered fashion, the product \({\textbf{A}}{\textbf{W}}\) again has block-wise symmetric entries. Iterative application of this multiplicative invariance to
shows that the column vectors \({\textbf{Q}}_{lj}\) and \({\textbf{L}}_{lj}\) in (50) are also symmetric.
Next, the scalar product \({\textbf{b}}^{\mathop {\textrm{T}}}{\textbf{d}}\in \mathbb {C}\) of a symmetric vector \({\textbf{d}}\) and an arbitrary vector \({\textbf{b}}\) of appropriate size is considered. The operator \(\mathop {\textrm{flip}}{{\textbf{b}}}\) reverses the order of entries of a vector \({\textbf{b}}\). Element-wise evaluation shows that
Defining \({\hat{{\textbf{c}}}}_{l, \textrm{sym}} = \frac{1}{2}\left( {\hat{{\textbf{c}}}}_l + \mathop {\textrm{flip}}{\overline{{\hat{{\textbf{c}}}}}_l}\right) \) and using the above relation yields
and analogously for \({\textbf{L}}_{ij}\). As \({\textbf{R}}\) is constructed from summands of this form via (49)–(52), the proposition follows. \(\square \)
A purely real matrix \({\textbf{R}}_{\textrm{sym}}\) will necessarily have a Frobenius norm smaller or equal than the norm of a matrix with same real part and arbitrary imaginary part. Hence, Proposition 4 allows to easily construct a minimizer that satisfies all constraints in case a different minimizer is returned in the quadratic program (56).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bayer, F., Leine, R.I. Sorting-free Hill-based stability analysis of periodic solutions through Koopman analysis. Nonlinear Dyn 111, 8439–8466 (2023). https://doi.org/10.1007/s11071-023-08247-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-023-08247-7