Experimental investigation of a single-degree-of-freedom system with Coulomb friction

Abstract

This paper presents an experimental investigation of the dynamic behaviour of a single-degree-of-freedom (SDoF) system with a metal-to-metal contact under harmonic base or joined base-wall excitation. The experimental results are compared with those yielded by mathematical models based on a SDoF system with Coulomb damping. While previous experiments on friction-damped systems focused on the characterisation of the friction force, the proposed approach investigates the steady response of a SDoF system when different exciting frequencies and friction forces are applied. The experimental set-up consists of a single-storey building, where harmonic excitation is imposed on a base plate and a friction contact is achieved between a steel top plate and a brass disc. The experimental results are expressed in terms of displacement transmissibility, phase angle and top plate motion in the time and frequency domains. Both continuous and stick-slip motions are investigated. The main results achieved in this paper are: (1) the development of an experimental set-up capable of reproducing friction damping effects on a harmonically excited SDoF system; (2) the validation of the analytical model introduced by Marino et al. (Nonlinear Dyn, 2019. https://doi.org/10.1007/s11071-019-04983-x) and, particularly, the inversion of the transmissibility curves in the joined base-wall motion case; (3) the systematic observation of stick-slip phenomena and their validation with numerical results.

1 Introduction

Friction plays a central role in many engineering systems, ranging from civil to mechanical applications. The main research interest in this field is the development of a predictive model for frictional joint behaviour: the challenge is rooted in the lack of understanding of the phenomenon across small and large scales [2]. As the Coulomb friction model has not proved sufficient to address accurately the dynamic regimes commonly experienced by engineering structures [2], most of the recent studies have focused on proposing alternative constitutive laws. These can account for friction-related effects not addressed such as stiction, friction dependence on sliding speed and hysteresis [3]. Stribeck [4, 5], LuGre [6, 7] or rate-and-state [8,9,10] models account for different combinations of these phenomena.

In the literature, experimental approaches have been used for three main different purposes: friction model development [11, 12], identification of existing models and/or parameters [13,14,15] or model validation [3, 16,17,18]. Attempts to characterise the friction force include models simply based on the friction coefficient $\mu$ (the coefficient of proportionality between friction force and normal force acting on the contact) [19, 20] or on more complicated constitutive laws which attempt to account for the dynamic friction component as well. Frequency dependency of $\mu$ is of interest for the analysis of jointed structures [21, 22]. It is not yet clear which underlying physical agents generate this dependency [23].

Experiments involving friction usually offer poor reliability and repeatability [3]. An effective solution is to consider alternative metrics during a test. For instance, the frictional frequency response (i.e. the ratio between the dynamic component of the friction force and sliding velocity fluctuations) has been used in references [3, 11, 23, 24].

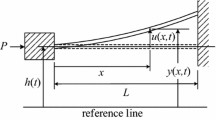
Several analytical and numerical approaches have been developed for investigating the response of structures with friction damping considering different constitutive laws. The dynamic response to forced vibration is not known analytically, even when applying Coulomb friction to a simple mass–spring system. Analytical approaches based on a Coulomb damping model, proposed by Den Hartog [25], Hong and Liu [26, 27] and other authors [16, 28,29,30,31,32], allow the investigation of the dynamic behaviour of such a system. Particularly, Den Hartog determined analytically a condition for identifying the motion regime (continuous or stick-slip) and the amplitude and phase angle of mass non-sticking response. Den Hartog’s solution has recently been extended by Marino et al. [1] to two classes of base motion problems, where friction contact is achieved between the mass and either a ground-fixed (Fig. 1a) or base-fixed (Fig. 1b) wall. In the second case, indicated as joined base-wall motion, the behaviour of the system exhibits significative differences compared to typical forced vibration cases, highlighting a more complex behaviour in terms of motion regimes and an inversion of the friction damping effect on the response amplitude when the exciting frequency is larger than 1.5 times the natural frequency of the system. This phenomenon introduces an interesting physical similarity with viscous single-degree-of-freedom (SDoF) systems (see reference [33]).

Experimental investigation of these SDoF systems with a Coulomb friction contact has received little attention [16, 34]. These experiments focus on the dynamic response in the time domain, mainly referring to stick-slip regime; to the best of the authors’ knowledge, only Marui and Kato [16] introduced the displacement transmissibility among their results but only for quasi-static motion. Furthermore, forced vibration testing has been performed exploiting base excitation but no experiments have been led for the joined base-wall motion case.

This paper presents an experimental investigation of a SDoF system under base and joined base-wall harmonic motion. The main goals of this contribution are:

• the development of an experimental framework suitable for reproducing a SDoF system;

• the validation of the analytical and numerical findings presented in [1];

• the investigation of continuous and stick-slip motions in the time and frequency domains, and their comparison with results found with a numerical approach.

Analytical results from [1] are reviewed in Sect. 2 and a numerical approach is also described; Sect. 3 is dedicated to the description of the experimental framework and of the testing procedure, as well as to the estimation of the parameters related to the SDoF model of the set-up; an overview of the experimental results is presented in Sect. 4, while Sect. 5 shows a detailed comparison between experimental and numerical results in time and frequency domains.

Fig. 1

SDoF mass–spring systems with a Coulomb friction contact

2 Mathematical models

In reference [1], Marino et al. introduced analytical and numerical approaches for the investigation of the dynamic behaviour of a SDoF system with Coulomb damping under harmonic base motion (Fig. 1a) or joined base-wall motion (Fig. 1b). This section recalls the main analytical findings presented in [1] and describes a numerical approach.

2.1 Summary of analytical developments

The analytical approach proposed by Den Hartog in reference [25] is able to address forced vibration in a SDoF system with Coulomb damping, represented in Fig. 1c. The equation of motion of a system with mass m, stiffness k, subject to a normal force N acting on the friction contact and a harmonic force of magnitude $F_0$ and frequency $\omega _\mathrm {b}$ applied to the mass can be written as:

$$\begin{aligned} m\ddot{x}+kx+\mu N\mathrm {sgn}(\dot{x})=F_0\cos (\omega _\mathrm {b}t) \end{aligned}$$

(1)

where $\mu$ is the friction coefficient between the mass and the wall. In the assumptions of a periodic and steady mass motion, Den Hartog determined:

• an analytical boundary condition for continuous non-sticking motion;

• for a continuous motion, analytical expressions of the mass steady response amplitude and phase angle.

The base motion problems in Fig. 1a, b are described, respectively, by the following governing equations:

$$\begin{aligned}&m\ddot{x}+kx+\mu N\mathrm {sgn}(\dot{x})=kY\cos (\omega _\mathrm {b}t) \end{aligned}$$

(2)

$$\begin{aligned}&m\ddot{z}+kz+\mu N\mathrm {sgn}(\dot{z})=kYr^2\cos (\omega _\mathrm {b}t) \end{aligned}$$

(3)

where Y is the amplitude of the base motion and $z=x-y$ is the relative motion between mass and wall. As explained in [1, 16], it is possible to describe the dynamic behaviour of these systems referring to two dimensionless groups only. These groups are the frequency ratio:

$$\begin{aligned} r=\dfrac{\omega _\mathrm {b}}{\omega _\mathrm {n}} \end{aligned}$$

(4)

i.e. the ratio between the driving frequency and the natural frequency $\omega _\mathrm {n}=\sqrt{k/m}$, and the force ratio:

$$\begin{aligned} \beta =\dfrac{\mu N}{kY} \end{aligned}$$

(5)

that is the ratio between the amplitudes of friction and exciting forces.

Comparing Eqs. (1) and (2), the base motion problem represented in Fig. 1a is equivalent to the forced vibration problem described by Den Hartog by posing $F_0=kY$. In particular, it can be found [1] that a steady motion is always possible if $\beta <1$ and the mass will exhibit a non-stop motion if:

$$\begin{aligned} \beta <\sqrt{\dfrac{V^2}{\bigg (\dfrac{S}{r^2}\bigg )^2+U^2}} \end{aligned}$$

(6)

where:

$$\begin{aligned}&U(r)=\dfrac{\sin (\pi /r)}{r[1+\cos (\pi /r)]} \end{aligned}$$

(7)

$$\begin{aligned}&V(r)=\dfrac{1}{1-r^2} \end{aligned}$$

(8)

$$\begin{aligned}&S(r) =\max \limits _{\tau _\mathrm {n}\in [0, {\pi \over r}]}\bigg \{\dfrac{r\sin (\tau _\mathrm {n})+Ur^2[\cos (r\tau _\mathrm {n})-\cos (\tau _\mathrm {n})]}{\sin (r\tau _\mathrm {n})}\bigg \}\nonumber \\ \end{aligned}$$

(9)

where:

$$\begin{aligned} \tau _\mathrm {n}=\omega _\mathrm {n}t \end{aligned}$$

(10)

is the dimensionless time. Displacement transmissibility and phase angle between response and excitation can be evaluated as [1]:

$$\begin{aligned} \dfrac{|X|}{|Y|}= & {} \sqrt{V^2-\big (U\beta \big )^2} \end{aligned}$$

(11)

$$\begin{aligned} \phi _\mathrm {xy}= & {} \arccos \bigg (\dfrac{1}{V}\dfrac{|X|}{|Y|}\bigg ) \end{aligned}$$

(12)

Den Hartog’s solution can be extended to joined base-wall motion case (Fig. 1b), since Eq. (3) has the same form as Eq. (1) with $F_0=kYr^2$. The amplitude of the excitation is here dependent on the frequency ratio and this implies a more complex scenario in terms of motion regimes, which can be described as follows [1]:

where:

$$\begin{aligned} \beta _\mathrm {lim}=r^2\sqrt{\dfrac{V^2}{\bigg (\dfrac{S}{r^2}\bigg )^2+U^2}} \end{aligned}$$

(14)

While Den Hartog’s solution can be applied only to relative mass–wall motion, mass absolute motion is also addressed in [1], so that displacement transmissibility and phase angle can be written as:

$$\begin{aligned} \dfrac{|X|}{|Y|}= & {} \max \limits _{\tau _\mathrm {n}\in [0, {\pi \over r}]}\bigg |\sqrt{V^2-\bigg (\dfrac{U\beta }{r^2}\bigg )^2}\cos (r\tau _\mathrm {n})\nonumber \\&+\beta [1-\cos (\tau _\mathrm {n})]-\dfrac{U\beta }{r^2}[r^3\sin (\tau _\mathrm {n})-\sin ( r\tau _\mathrm {n})]\bigg |\nonumber \\ \end{aligned}$$

(15)

$$\begin{aligned} \phi _\mathrm {xy}= & {} \arccos \Bigg [\dfrac{1}{V}\sqrt{V^2-\bigg (\dfrac{U\beta }{r^2}\bigg )^2}\Bigg ]+r\tau _\mathrm {n,max}-\pi \nonumber \\ \end{aligned}$$

(16)

where $\tau _\mathrm {n,max}$ is the dimensionless time where the maximum absolute response occurs during a steady motion cycle.

2.2 Numerical procedure

The analytical results summarised in Sect. 2.1 can be used to investigate the displacement transmissibility and the phase angle for continuously sliding motions but a numerical approach is required to describe the full dynamic response of the system, including stick-slip solutions.

Due to the non-smooth nature of the system, specialised numerical solvers (stiff solvers) can be implemented in order to improve both the accuracy and the computational efficiency when stick-slip motion occurs. Alternatively, it is possible to use standard integration methods by setting explicit conditions to account for the transition between different regimes. The latter approach is implemented here.

The governing equations Eqs. (2), (3) are written in a non-dimensional form:

$$\begin{aligned} r^2\bar{x}''+\bar{x}+\beta \mathrm {sgn}(\bar{x}')=\cos (\tau _\mathrm {b}) \end{aligned}$$

(17)

for the base motion case and:

$$\begin{aligned} r^2\bar{z}''+\bar{z}+\beta \mathrm {sgn}(\bar{z}')=r^2\cos (\tau _\mathrm {b}) \end{aligned}$$

(18)

for the joined base-wall motion case, so that the numerical response can be evaluated for different pairs of the parameters r and $\beta$, without need to specify any other system parameters. In the above equations, the dimensionless time:

$$\begin{aligned} \tau _\mathrm {b}=\omega _\mathrm {b}t \end{aligned}$$

(19)

and the dimensionless displacements:

$$\begin{aligned}&\bar{x}=\dfrac{x}{Y}\qquad \qquad&\bar{z}=\dfrac{z}{Y} \end{aligned}$$

(20)

are introduced and $\bullet '=\mathrm {d}\bullet /\mathrm {d}\tau _\mathrm {b}$. It is worth noting that, in this formulation, the duration of an excitation cycle is always equal to $2\pi$. Therefore, the final time of the integration can be expressed as:

$$\begin{aligned} \tau _\mathrm {b,f}=2\pi N_\mathrm {cycles} \end{aligned}$$

(21)

and the user can choose directly the number of cycles ($N_\mathrm {cycles}$) to be included in the simulation.

Fig. 2

Pictures of the test rig. A rotor is connected to the base plate of a single-storey building through a Scotch yoke mechanism. A counterweight pinned to the external frame (a) or to the base plate (b) applies a normal force on the top plate

In this paper, Eqs. (17), (18) are numerically integrated by using a variable-step Runge–Kutta (4,5) method, implemented in MATLAB by the function ode45 [35]. The integration is performed until the condition for which mass sticking occurs is verified with an absolute tolerance of $10^{-6}$. In such a way, the governing equation are solved numerically only when the motion is smooth. Specifically, the stop condition occurs in mass motion when [32]:

Eq. (22b) can be also written as:

$$\begin{aligned} |\cos (\tau _\mathrm {b})-\bar{x}(\tau _\mathrm {b})|\le \beta \end{aligned}$$

(23)

The condition (22a) is clearly verified for the whole duration of the stop, so mass sticking will last as long as the condition (23) holds. Therefore, the transition from sticking to slipping phase will occur when:

$$\begin{aligned} |\cos (\tau _\mathrm {b})-\bar{x}(\tau _\mathrm {b})|-\beta =0 \end{aligned}$$

(24)

The value of $\tau _\mathrm {b}$ for which Eq. (24) is satisfied is determined by using the MATLAB function fzero [35] with an absolute tolerance of $10^{-6}$. Starting from this time instant, Eqs. (17), (18) will be solved again with ode45, considering the latest values of $\bar{x}$ and $\bar{x}'$ as initial conditions. The described procedure is repeated until $\tau _\mathrm {b}=\tau _\mathrm {b,f}$.

The evaluation of the frequency spectrum of the response and, in general, of frequency related quantites, requires the interpolation of the numerical responses on a fixed-step time vector. The length of such a step will be the inverse of the sampling frequency, which can be specified by the user. The corresponding time step has also been added to ode45 as a maximum step condition.

The displacement transmissibility and the phase angle are determined by comparing peak values in the frequency spectrum of the base and mass motions, as explained in detail in Sect. 3.2.3 for the experimental signals. The results obtained from this numerical procedure are presented in Sect. 4, 5.

3 Experimental approach

3.1 Apparatus

The test rig is a single-storey building composed by two metal plates connected through four metal bars, as shown in Fig. 2a, b. Each stanchion is doubly bolted to both the floors. The main properties of these components are reported in Table 1.

Table 1 Properties of the single-storey building components

A friction force is applied to the system by means of a brass disc resting on the top plate producing a line metal-to-metal contact. The disc is mounted on a bar equipped with a counterweight system, so that the normal force, and therefore the friction force, applied on the plate can be modified by adjusting the position of the weights along the bar.

Two test configurations are considered by changing the location of the counterweight system. When the counterweight is pinned to the external frame (as shown in Fig. 2a), the fixed wall configuration is obtained. The joined base-wall configuration (shown in Fig. 2b) is instead achieved by pinning the counterweight system to a post bolted to the base plate. A schematic representation of the test rig is reported in Fig. 3.

The single-storey building is dynamically excited through the motion of the base plate. In particular, this motion is imposed by using an electric motor (DKM-9PBK) with an inverter motor speed regulator (RS Pro RS510) and a Scotch yoke mechanism in order to convert the rotating motion into a harmonic reciprocating motion. The frequency of the base motion can be controlled by changing the input speed of the inverter, while the amplitude can be set by pinning the Scotch yoke to different points of the rotor.

During the test, the displacements of the base and top plates were recorded with two separate laser displacement sensors (optoNCDT 1420, with a measuring range of 50 mm [36]). The sensors were clamped to the external frame.

3.2 Test procedure

3.2.1 Parameter estimation and setting

The single-storey building can be modelled as a SDoF mass–spring system equivalent to those shown in Fig. 1a, b. In a first approximation, the top plate corresponds to the mass m of the SDoF, while the four stanchions can be modelled with an equivalent spring of stiffness k. The last statement requires two important assumptions:

• the stiffness of the plates, compared to the flexural stiffness of the stanchions, is large enough to consider them as infinitely rigid;

• the driving frequencies investigated during the test are such that only the first bending mode of the stanchions can be excited.

Both assumptions are satisfied with the present experimental set-up. The approximate mass and the stiffness of the SDoF system can be calculated as follows:

• the equivalent stiffness of the system is the overall stiffness provided by the four stanchions. The stiffness of each stanchion can be therefore calculated, in a first approximation, as the stiffness of a beam clamped to both the plates;

• because of their deformed shape during vibration, a fraction of the mass of the stanchions will participate to the mass motion. Therefore, this contribution should be added to the mass of the top plate for estimating the equivalent mass of the SDoF system.

Fig. 3

Schematic representation of the base motion test rig in the ground-fixed wall configuration

However, as shown in Eqs. (17), (18), the dynamic response of the system, both to base and to joined base-wall harmonic excitations, is a function of the dimensionless parameters r and $\beta$; these parameters can be directly estimated experimentally as follows.

The frequency ratio r requires the evaluation of $\omega _\mathrm {b}$ and $\omega _\mathrm {n}$. The driving frequency is specified by changing the input frequency of the inverter and it can be visualised from the frequency spectrum of the excitation, which will exhibit a peak at $f=\omega _\mathrm {b}/2\pi$. The natural frequency has been estimated by running multiple tests at different driving frequencies up to 8 Hz in the absence of friction, i.e. removing the counterweight from the set-up. A least square method was used to find the value of $\omega _\mathrm {n}$ for which the difference between the experimental transmissibility and the analytical transmissibility [32]

$$\begin{aligned} \dfrac{|X|}{|Y|}=\dfrac{1}{|1-r^2|} \end{aligned}$$

(25)

is minimum.

It is possible to observe in Fig. 4 a very good agreement between experimental and analytical results when the natural frequency is set to 3.086 Hz. The transmissibility results shown in Fig. 4 also highlight how the experimental apparatus is suitable for the representation of a SDoF system.

Fig. 4

Undamped displacement transmissibility: experimental (markers) versus analytical (continuous line)

The force ratio can be adjusted by choosing a configuration of the counterweight masses producing the desired normal force on the top plate. The friction force acting between the disc and the top plate cannot be directly measured during the forced vibration test. Nevertheless, the coefficient $\mu$ can be estimated by using a linear decrement approach. A free vibration is generated in the building by pulling and releasing the top mass and, in accordance with the Coulomb model for free vibration, the peaks of each cycle of the measured freely decaying vibration have an approximately linear slope (Fig. 5). Therefore, the friction coefficient can be evaluated as [32]:

$$\begin{aligned} \mu =\dfrac{k(x_1-x_2)}{4N} \end{aligned}$$

(26)

where $x_1$ and $x_2$ are the displacements of two subsequent peaks. A better estimate can be obtained by averaging the coefficient estimated for every pairs of subsequent peaks of the signal.

Fig. 5

Experimental measurement of top plate free decay. The measured peaks show an approximately linear slope (dashed line)

Unlike the friction coefficient, the force ratio can be directly estimated from linear decrement once the base motion amplitude Y has been selected. In fact, recalling Eq. 5 and writing the normal force as $N=Mg$, where M is the effective mass produced by the counterweight system on the contact line, the force ratio can be written as:

$$\begin{aligned} \beta =\dfrac{\mu Mg}{kY} \end{aligned}$$

(27)

and, from Eqs. 26 and  27:

$$\begin{aligned} \beta =\dfrac{x_1 - x_2}{4Y} \end{aligned}$$

(28)

It is worth noting that the expression for the force ratio is only valid under the assumption of a Coulomb friction model. Therefore, efforts have been made to reduce and control non-Coulomb phenomena which may occur during the test campaign. In particular, the set-up allows the modification of the contact line between the disc and upper plate when significant wear has occurred; in fact, the brass disc can be rotated or shifted. Furthermore, debris was removed after each test by thoroughly cleaning the surfaces in contact.

3.2.2 Further considerations on the force ratio estimation

In order to verify the theoretical results presented in [1] two response metrics need to be considered: the displacement transmissibility and the phase lag.

For a fixed frequency ratio, the force ratio estimated from the linear decrement can be initially used. However, during the test campaign the friction force might vary. This can be due to variations in the normal force [37] and/or in the friction coefficient. Particularly, it is worth observing that the latter is an empirical parameter and its variation can be due to several underlying physical agents, as stated in Sect. 1.

Fig. 6

Counterweight system pinned to the external frame (a) and to the base-fixed post (b)

Fig. 7

Time domain evolution of base and mass displacements for a Coulomb damped SDoF system under harmonic base motion at ($r=0.85$, $\beta =0.2$) before and after signal post-processing

Fig. 8

Frequency spectra of base and mass displacements for a Coulomb damped SDoF system under harmonic base motion at ($r=0.85$, $\beta =0.2$) before and after signal post-processing

The normal force variation can be related to an imperfect pin connection between the counterweight bar and either the external frame (base motion case, see Fig. 6a) or the base-fixed post (joined base-wall motion case, shown in Fig. 6b). In fact, this constraint should allow a free rotation around the pinning axis, preventing at the same time any horizontal or vertical displacement of the counterweight bar. Washers have been located on both sides of the pinning disc of the counterweight system in order to aid the rotation. Even so, pinning these components too tightly may partially prevent this free rotation, producing a reaction moment in the constraint, which would eventually alter the normal force applied on the plate. On the other hand, an excessively loose tightening would allow an unacceptable horizontal displacement of the counterweight bar. Consequently, in order to limit both effects, care was taken when tightening.

The friction coefficient displayed only small variations from test to test under the same conditions. However, some differences were observed when varying the driving frequency. The focus of this study is not to quantify this variation but, as stated at the beginning of this section, to validate general results in terms of dimensionless groups.

Therefore, the force ratio estimated from the linear decrement is verified, and possibly refined, to compensate for friction force variations, to yield simultaneously a good agreement with both displacement transmissibility and phase angle theoretical results. This is achieved by controlling the normal force applied with the counterweight. It is worth noting that since it is possible to reproduce not only the magnitude but also the phase shift of the response, and therefore the main harmonic component of the mass motion, the force ratio fine tuning considered is not affecting the validation provided by the experiment.

3.2.3 Signal processing for response metrics evaluation

The signals acquired during the test have to be processed in order to evaluate accurately the driving frequency, and therefore the frequency ratio. In particular, the signals from the laser sensors are recorded for $60\,\mathrm {s}$ with a sampling frequency of $2\,\mathrm{kHz}$. This choice of duration for the recording window represents a compromise between obtaining an acceptable frequency resolution and avoiding significant changes in the friction force due to wear and debris formation during a single test.

Signals were processed by applying a Hanning window and then zero-padding in order to reduce leakage [38] and allow a more accurate resolution of the main peaks in the frequency spectrum by increasing the frequency resolution. Figures 7, 8 show how post-processing affects a pair of recorded signals (with parameters specified in the figure caption) both in time and frequency domains, respectively. It is worth noting that the frequency domain signal displays not only a peak at the main driving frequency, but also smaller peaks at other frequencies. This is because the set-up is generating mainly a mono-harmonic base motion but also other harmonics are excited, as inevitable when using a Scotch yoke mechanism. Nevertheless, these additional frequency contents are typically more than 20 dB below the fundamental peak so they do not affect the evaluation of the response metrics, which are always referred to the main driving frequency, as detailed in what follows. The displacement transmissibility is evaluated as:

$$\begin{aligned} \mathrm {Tr}_{r,\beta }=\dfrac{|\hat{X}_{r,\beta }(f_b)|}{|\hat{Y}_r(f_b)|} \end{aligned}$$

(29)

where $\hat{X}_{r,\beta }(f)$ and $\hat{Y}_{r}(f)$ are, respectively, the frequency spectra of the processed mass and base displacements for a specific couple of frequency and force ratios. The phase shift between excitation and response can be calculated as:

$$\begin{aligned} \phi _{r,\beta } = \arg \{\hat{X}_{r,\beta }(f_b)\}-\arg \{\hat{Y}_r(f_b)\} \end{aligned}$$

(30)

Fig. 9

Displacement transmissibility of a Coulomb damped SDoF system under harmonic base motion for varying force ratios: analytical (dotted line), numerical (circles) and experimental (crosses). Analytical mass motion is continuous above Den Hartog’s boundary (continuous line) while stick-slip motion occurs below it

Fig. 10

Displacement transmissibility of a Coulomb damped SDoF system under harmonic base motion: experimental (markers) versus analytical (continuous lines). Analytical mass motion is continuous above Den Hartog’s boundary (dotted line) while stick-slip motion occurs below it

Fig. 11

Displacement transmissibility of a Coulomb damped SDoF system under harmonic base motion in the low-frequency-ratio region: experimental (markers) versus numerical (continuous lines)

Fig. 12

Phase angle of a Coulomb damped SDoF system under harmonic base motion: experimental (markers) versus analytical (continuous lines)

4 Transmissibility and phase angle results

4.1 Base motion with fixed wall

The base motion case was investigated using the rig shown in Fig. 2a. In addition to the two laser sensors introduced in Sect. 3.1, the set-up was equipped with a third laser sensor clamped to the external frame to measure the motion of the disc and ensure that it was negligible. For every test performed, it was verified that the amplitude of the disc motion was at least two orders of magnitude smaller than top plate vibration.

The parameter space investigated was $r=0.025:2.5$ and $\beta =[0.2,0.4,0.6]$. Overall results from the experimental campaign on the base motion case are reported in Figs. 9, 10, 11, 12 and 13. The displacement transmissibility as a function of the frequency ratio is shown in Fig. 9. The experimental results are compared with the analytical and numerical results showing an excellent agreement when the motion is continuous. Den Hartog’s analytical boundary between continuous and stick-slip motion [25] is reported in the same figure.

Fig. 13

Phase angle of a Coulomb damped SDoF system under harmonic base motion in low-frequency-ratio region: experimental (markers) versus numerical (continuous lines)

The numerical results for the displacement transmissibility have been obtained by using the approach described in Sect. 2.2. In particular, since the decay rate of the transient response may be slow due to the absence of viscous damping, the duration of the overall simulation was varied for each numerical analysis. The overall duration was set so that, after reaching a steady-state condition within a base motion cycle, additional 100 steady-state response cycles were considered. The transmissibility evaluation was then performed on these 100 cycles, disregarding the initial transient.

The results obtained for the three different $\beta$ values are shown in Fig. 10. The low-frequency-ratio region where stick-slip motion occurs is represented in Fig. 11, where a comparison between experimental and numerical results shows an overall good agreement. Particularly, it can be observed that for low values of $\beta$ the experimental results are better matched by the numerical solution. The main disagreement is found in the range $r=0.3:0.6$, where the experimental results appear to be overlapped rather than showing the increase of the displacement transmissibility forecast by the numerical solution.

In Fig. 12, the phase angle between base and mass motion is shown as a function of the inverse frequency ratio. The agreement between analytical and experimental results is also very good. In Fig. 13, it is shown that, similarly to what observed for the transmissibility, the agreement between experimental and numerical phase angles is acceptable but less accurate in the low-frequency-ratio region when the force ratio increases. It is possible to observe that the phase angle is more sensitive than the displacement transmissibility to the force ratio variations; so it appears to be a more suitable metric for the force ratio detection in experimental measurements.

Fig. 14

Displacement transmissibility of a Coulomb damped SDoF system under harmonic joined base-wall motion for varying force ratios: analytical (dotted line), numerical (circles) and experimental (crosses). Three different motion regimes are identified analytically by Eqs. (13a, b, c): no steady motion (dark-grey region), relative mass–wall stick-slip motion (light-grey region) and continuous motion (white region)

Fig. 15

Displacement transmissibility of a Coulomb damped SDoF system under harmonic joined base-wall motion: experimental (markers) versus analytical (continuous lines) (a) and detail of the inversion (b)

Moreover, it is worth noting that, according to theory [1], stick-slip motion at high frequency ratios would occur only for $\beta =0.6$ among the investigated cases. This has been verified experimentally. In Figs. 9c and 12, it can be observed how the transmissibility and the phase angle trends change suddenly after the intersection with Den Hartog’s boundary.

4.2 Joined base-wall motion

The joined base-wall motion case was investigated on the set-up shown in Fig. 2b. An additional laser sensor clamped to the external frame was used to measure the displacement of the disc to ensure that the “wall”was providing the same motion as the base. It was observed that the disc motion was characterised by a negligible phase shift with respect to the base motion and a very low percentage increase in the level of noise.

The parameters space investigated was such that $\beta =[0.5,0.75,1,1.5,2]$, while values for r ranged up to 2.5. The results of this experimental campaign are presented in Figs. 14, 15 and 16. In Fig.14, the displacement transmissibility is illustrated as a function of r, showing an excellent agreement among experimental, analytical and numerical results. According to the theoretical boundaries introduced in Sect. 2, three motion regimes can be distinguished for every value of $\beta$: no steady motion (dark-grey region), relative mass–wall stick-slip motion (light-grey region) and continuous motion (white region). The experimental transmissibilities obtained for the different values of $\beta$ investigated are compared in Fig. 15a. The experimental results confirmed the existence of a point of inversion across the transmissibility curves. This demonstrated that the resulting amplitude of the mass response is amplified by increasing the force ratio, which corresponds to increasing friction damping, above $r\cong 1.5$ [1]. The inversion point is shown in detail in Fig. 15b, where it is possible to observe that the experimental results obtained immediately to the left and to the right of $r=1.5$ display an inverted trend with varying $\beta$. It can also be noted that, despite the overall very good agreement, in the frequency ratio range represented in Fig. 15b there is a visible difference between experimental and analytical transmissibilities. Due to the low sensitivity to force ratio variation exhibited by the transmissibility in this range, it would not be possible to obtain an accurate force ratio identification.

In Fig. 16, the phase angle between base and mass motion is plotted versus the inverse frequency ratio, showing a very good agreement between analytical and experimental results. For $\beta =2$, it is possible to observe that, in relative stick-slip conditions, the phase angle changes suddenly, showing increasing values for lower frequency ratios.

4.3 Limitations on the applicability of the set-up

The results presented in the previous subsections for base and joined base-wall motion cases have shown that the SDoF Coulomb friction system can be investigated with the proposed experimental set-up.

Fig. 16

Phase angle of a Coulomb damped SDoF system under harmonic joined base-wall motion: experimental (markers) versus analytical (continuous lines)

Fig. 17

Experimental time response at ($r=1.15$, $\beta =0.7$), highlighting a mass–disc sticking occurrence at $t=54.8s$

However, during the test campaign, it was observed that for some particular conditions the top plate and the disc became stuck during the test. For example, in Fig. 17, it is shown a case for which the mass and disc coupling affects the mass motion to the point of reaching a no-motion condition after about 55s. It is worth noting that a steady-state condition is apparently reached in a first stage but this is followed by a variation in set-up conditions which leads to a new transient ending with the sticking condition. In order to investigate the stop occurrence, the test was repeated under the same conditions. It was found that the duration of the motion length was changing in every test; furthermore, this event might occur outside the duration of the test (60 s). It was not possible to determine the causes of this phenomenon, which might include: (1) initial conditions variation; (2) contact properties variation; (3) temperature variation; (4) debris formation; (5) set-up imperfections; (6) transient chaotic behaviour (see reference [40]). Moreover, it is worth noting that, starting a new test directly from the stuck condition, no mass motion was observed.

The particular test conditions for which this phenomenon was observed are discussed in what follows. In the base motion with fixed wall case, it occurred for values above $\beta \cong 0.7$, independent of the frequency ratio. As for the joined base-wall motion case, mass–disc sticking may occur for any force ratio for certain values of r. Introducing an equivalent force ratio:

$$\begin{aligned} \beta _\mathrm {BW}=\dfrac{\mu N}{kYr^2}=\dfrac{\beta }{r^2} \end{aligned}$$

(31)

as the ratio between the amplitudes of the friction force and of the equivalent force applied on the mass, the no-motion phenomenon was observed again above $\beta _\mathrm {BW}\cong 0.7$.

It is also worth noting that, because of the mass–disc sticking during the test, it is difficult to achieve an accurate experimental evaluation of the response metrics within the stick-slip region shown in Fig. 14. In particular, the lowest frequency ratio for which continuous or stick-slip motion was observed at least for 60 s for a given value of $\beta$ is shown in the frequency ratio-force ratio plane represented in Fig. 18. It can be observed that stick-slip motion was experimentally investigated only for $\beta =2$.

In conclusion, this set-up cannot be used to investigate with sufficient accuracy the displacement transmissibility and phase angle when $\beta \ge 0.7$ in the base motion configuration and $\beta _\mathrm {BW}\ge 0.7$ in the joined base-wall motion case.

Fig. 18

$\beta _\mathrm {BW}$ curves (grey continuous lines) in the frequency ratio–force ratio plane. Experimental $\beta _\mathrm {BW}$ values (markers). The boundary condition between continuous and stick-slip motion (dotted line) is given by Eq. 14

Fig. 19

Time mass steady-state response for $\beta =0.2$ (short duration): experimental (black line) versus numerical (red line). (Color figure online)

Fig. 20

Time mass steady-state response for $\beta =0.2$ (long duration): experimental (black line) versus numerical (red line). (Color figure online)

Fig. 21

Frequency spectra of mass steady-state response for $\beta =0.2$: experimental (black line) versus numerical (red line). (Color figure online)

5 Mass motion analysis in the time and frequency domains

In this section, the experimental results obtained for fixed pairs of the parameters r and $\beta$ are compared to the system response yielded by the numerical approach in different motion regimes. Particularly, the mass stick-slip motion is investigated in the time and frequency domains in order to account for features such as the number of stops per cycle and their duration, as well as the multi-harmonic content, which cannot be captured by the response metrics presented in Sect. 4.

During the test, the signals were recorded for 60 s only after a steady-state condition was reached. For this reason, the experimental response in the time domain was shifted to match the first zero crossing of the numerical steady-state response.

The comparison between the experimental and numerical mass motions for fixed wall configuration is shown in Figs. 19, 20 and 21 for different values of r at $\beta =0.2$. A comparison in the time domain is shown in Fig. 19 for a small number of cycles in order to investigate the agreement in terms of number and duration of the stops, and the causes of the amplitude mismatches highlighted in the displacement transmissibility in Fig. 11b. It is possible to observe that the experimental mass responses are well reproduced by the numerical simulations, even in the complex case of a multiple stops stick-slip regime. The comparison between the same signals for longer durations is reported in Fig. 20. This allows the assessment of their overall agreement. The experimental mass motion shows the presence of a low-frequency variation not accounted by the numerical simulations. It is worth noting that an asymmetric mass motion with one stop per cycle is shown in Figs. 19b, 20b. This peculiar case of stick-slip motion was discussed in references [32, 40]. Particularly, an asymmetric solution is expected for $r=0.5$ when $\beta <1/3$ [32]. The numerical solutions presented in this paper confirm this result, which has also been observed experimentally. However, it is worth mentioning that when $r=0.5$ (or, more generally, $r=1/n, n=1,2,\ldots$), the numerical response exhibits a very long initial transient and it is possible that further changes may occur in the motion after the numerical simulation is stopped [32].

The comparison between experimental and numerical frequency spectra is shown in Fig. 21. The experimental noise level is below -40dB in all the reported cases and it allows a clear observation of the peaks. A very good agreement is observed for the peaks related to the first six odd harmonics. While these peaks are due to the nonlinearity of the problem [39], the peaks observed at the even harmonics in the experimental spectra are caused by the non-ideal mono-harmonic base motion, as discussed in Sect. 3.2.3. In Fig. 21b, even peaks are observed also in the numerical response and they are clearly due to the asymmetry in the mass motion. Finally, a difference in the low-frequency content can be observed between experimental and numerical signals, as shown in Fig. 21c–e. This can be due to set-up imperfections, noise from the instrumentation or variation in the test conditions.

In conclusion, it has been shown that the experimental set-up allows the investigation of the dynamic behaviour of a Coulomb friction oscillator also in the time and frequency domains. Particularly, the stick-slip motion has been observed with a very good accuracy.

6 Concluding remarks

An experimental investigation of a Coulomb friction oscillator under harmonic base excitation and joined base-wall excitation has been presented in this paper and validated with analytical and numerical results.

A single-storey building set-up with a metal-to-metal contact, in two different configurations, has been designed to apply simultaneously a harmonic base excitation and a static normal force. The response metrics considered were: (1) displacement transmissibility; (2) phase shift angle; (3) time domain and (4) frequency domain mass motion.

The analytical developments presented in reference [1] have been validated for different values of the frequency and force ratios. An excellent agreement with analytical results for the continuous motion has been found in terms of the response metrics (1) and (2). In particular, it was confirmed that, in the joined base-wall motion case, the transmissibility curves present an inversion point at $r\cong 1.5$.

A very good agreement between experimental and numerical results was obtained in terms of the four response metrics. In particular, it was shown that the numerical approach and the experimental set-up allow the observation of features such as the number and the duration of the stops in stick-slip regime, and the multi-harmonic content in the system response.

The main limitations of the test set-up were discussed. In particular, the frequency ratio–force ratio parameter space which can be investigated is limited by the occurrence of a sticking between the surfaces in contact when an equivalent force ratio (defined differently for each set-up configuration) is above 0.7.

Overall, the experimental investigation presented in this paper has shown that the theoretical approaches proposed in [1] are suitable, in most conditions, for describing the dynamic behaviour of a SDoF system with a metal-to-metal contact. It has been shown that by combining mathematical models with experimental measurements, it is possible to determine the force ratio and therefore the friction coefficient. Further work will focus on investigating with the proposed set-up different materials in contact, friction-related effects not accounted by Coulomb model and the transition between different stick-slip motion regimes.