Closed-form solutions for free vibration of rectangular FGM thin plates resting on elastic foundation

Abstract

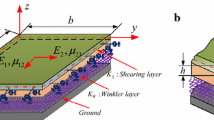
This article presents closed-form solutions for the frequency analysis of rectangular functionally graded material (FGM) thin plates subjected to initially in-plane loads and with an elastic foundation. Based on classical thin plate theory, the governing differential equations are derived using Hamilton’s principle. A neutral surface is used to eliminate stretching–bending coupling in FGM plates on the basis of the assumption of constant Poisson’s ratio. The resulting governing equation of FGM thin plates has the same form as homogeneous thin plates. The separation-of-variables method is adopted to obtain solutions for the free vibration problems of rectangular FGM thin plates with separable boundary conditions, including, for example, clamped plates. The obtained normal modes and frequencies are in elegant closed forms, and present formulations and solutions are validated by comparing present results with those in the literature and finite element method results obtained by the authors. A parameter study reveals the effects of the power law index n and aspect ratio a/b on frequencies.

Appendices

Appendix 1

Here the elastic foundation and in-plane loads are not involved. The dimensionless natural frequency parameter is $\omega ^{{*}}=\omega a^{2}\sqrt{\rho h/D}$. As for the SUS304 and $\hbox {Si}_{3}\hbox {N}_{4}$ plates, we have

$$\begin{aligned}&\omega _{{\mathrm{Si}_3 \mathrm{N}_4} }^{*} =\omega _{\mathrm{Si}_3 \mathrm{N}_4 } a^{2}\sqrt{\rho _{\mathrm{Si}_3 \mathrm{N}_4 } h/D_{\mathrm{Si}_3 \mathrm{N}_4 } } ,\nonumber \\&\omega _{\mathrm{SUS304}}^{*} =\omega _{\mathrm{SUS304}} a^{2}\sqrt{\rho _{\mathrm{SUS304}} h/D_{\mathrm{SUS304}} }. \end{aligned}$$

(A1)

From Eq. (24) one finds that the frequency parameter $\omega ^{{*}}$ is the same for thin plates with different materials since the elastic foundation and in-plane loads are not taken into account here, that is

$$\begin{aligned} \omega _{\mathrm{Si}_3 \mathrm{N}_4 }^{*} =\omega _{\mathrm{SUS304}}^{*}. \end{aligned}$$

(A2)

Substitution of Eq. (A1) into Eq. (A2) yields

$$\begin{aligned} \frac{\omega _{\mathrm{Si}_3 \mathrm{N}_4 } }{\omega _{\mathrm{SUS304}} }=\frac{\sqrt{\rho _{\mathrm{SUS304}} /D_{\mathrm{SUS304}} }}{\sqrt{\rho _{\mathrm{Si}_3 \mathrm{N}_4 } /D_{\mathrm{Si}_3 \mathrm{N}_4 } }}. \end{aligned}$$

(A3)

Yang and Shen [6] used the dimensionless natural frequency parameter $\omega ^{*}=\omega a^{2}\sqrt{\rho _{\mathrm{SUS304}} h/D_{\mathrm{SUS304}} }$ for plates with different materials, then

$$\begin{aligned}&\omega _{\mathrm{Si}_3 \mathrm{N}_4 }^{*} =\omega _{\mathrm{Si}_3 \mathrm{N}_4 } a^{2}\sqrt{\rho _{\mathrm{SUS304}} h/D_{\mathrm{SUS304}} }, \nonumber \\&\omega _{\mathrm{SUS304}}^{*} =\omega _{\mathrm{SUS304}} a^{2}\sqrt{\rho _{\mathrm{SUS304}} h/D_{\mathrm{SUS304}} }, \end{aligned}$$

(A4)

from which we have

$$\begin{aligned} \frac{\omega _{\mathrm{Si}_3 \mathrm{N}_4 }^{*} }{\omega _{\mathrm{SUS304}}^{*} }=\frac{\omega _{\mathrm{Si}_3 \mathrm{N}_4 } }{\omega _{\mathrm{SUS304}} }. \end{aligned}$$

(A5)

To substitute the material properties of SUS304 and $\hbox {Si}_{3}\hbox {N}_{4}$ as given in Table 3 into Eq. (A3), and to substitute the ensuing results into Eq. (A5), one can obtain that the ratio of the frequency parameter $\omega ^{*}$ between $\hbox {Si}_{3}\hbox {N}_{4 }$ and SUS304 is 2.2579 (Table 13). In Sect. 4.1, we use the same dimensionless natural frequency parameter as Yang and Shen [6] in numerical comparisons, $\omega _{\mathrm{Si}_3 \mathrm{N}_4 }^{*} / \omega _{\mathrm{SUS304}}^{*}$, which is also 2.2579 (Table 13); therefore, it can be concluded that the present results are correct. But using the numerical results of Yang and Shen [6], $\omega _{\mathrm{Si}_3 \mathrm{N}_4 }^{*} /\omega _{\mathrm{SUS304}}^{*}$ is 1.2164, and this shows that some numerical results of Yang and Shen [6] may not be correct.

Appendix 2

The differential operators in Eq. (18) are as follows

$$\begin{aligned} L_{11} \left( \right)= & {} A_{11} \frac{\partial ^{2}}{\partial x^{2}}+A_{66} \frac{\partial ^{2}}{\partial y^{2}}, \nonumber \\ L_{12} \left( \right)= & {} A_{12} \frac{\partial ^{2}}{\partial x\partial y}+A_{66} \frac{\partial ^{2}}{\partial x\partial y}, \nonumber \\ L_{13} \left( \right)= & {} -B_{11} \frac{\partial ^{3}}{\partial x^{3}}-\left( {B_{12} +2B_{66} } \right) \frac{\partial ^{3}}{\partial x\partial y^{2}}, \nonumber \\ L_{22} \left( \right)= & {} A_{66} \frac{\partial ^{2}}{\partial x^{2}}+A_{22} \frac{\partial ^{2}}{\partial y^{2}}, \nonumber \\ L_{23} \left( \right)= & {} -\left( {B_{12} +2B_{66} } \right) \frac{\partial ^{3}}{\partial x^{2}\partial y}-B_{22} \frac{\partial ^{3}}{\partial y^{3}} ,\nonumber \\ L_{33} \left( \right)= & {} D_{11} \frac{\partial ^{4}}{\partial x^{4}}+2\left( {D_{12} +2D_{66} } \right) \frac{\partial ^{4}}{\partial x^{2}\partial y^{2}}+D_{22} \frac{\partial ^{4}}{\partial y^{4}}, \nonumber \\ L_{34} \left( \right)= & {} -\left( {F_x \frac{\partial ^{2}}{\partial x^{2}}+2F_{xy} \frac{\partial ^{2}}{\partial x\partial y}+F_y \frac{\partial ^{2}}{\partial y^{2}}} \right) , \nonumber \\&\nabla ^{2}=\frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}. \end{aligned}$$

(A6)

And the boundary conditions derived using Hamilton’s principle have the following forms:

$$\begin{aligned}&\left. {\left( {N_x \delta u_0 +N_{xy} \delta v_0 } \right) } \right| _0^a =0, \nonumber \\&\left. {\left( {N_y \delta v_0 +N_{xy} \delta u_0 } \right) } \right| _0^b =0, \nonumber \\&\left. \left[ Q_x +\frac{\partial M_{xy} }{\partial y}+F_{xy} \frac{\partial w}{\partial y}+(K_2 +F_x )\frac{\partial w}{\partial x}\right. \right. \nonumber \\&\quad \left. \left. + \, \left( {I_1 \frac{\partial ^{2}u_0 }{\partial t^{2}}-I_2 \frac{\partial ^{3}w}{\partial x\partial t^{2}}} \right) \right] \delta w \right| _0^a =0,\nonumber \\&\left. \left[ Q_y +\frac{\partial M_{xy} }{\partial x}+F_{xy} \frac{\partial w}{\partial x}+(K_2 +F_y )\frac{\partial w}{\partial y}\right. \right. \nonumber \\&\quad \left. \left. + \, \left( {I_1 \frac{\partial ^{2}v_0 }{\partial t^{2}}-I_2 \frac{\partial ^{3}w}{\partial y\partial t^{2}}} \right) \right] \delta w \right| _0^b =0,\nonumber \\&\left. {M_x \frac{\partial \delta w}{\partial x}} \right| _0^a =0 ,\nonumber \\&\left. {M_y \frac{\partial \delta w}{\partial y}} \right| _0^b =0, \nonumber \\&\left. {\left. {2M_{xy} \delta w} \right| _0^a } \right| _0^b =0. \end{aligned}$$

(A7)

The shear forces are given by following relations:

$$\begin{aligned} Q_x= & {} \frac{\partial M_x }{\partial x}+\frac{\partial M_{xy} }{\partial y}, \nonumber \\ Q_y= & {} \frac{\partial M_y }{\partial y}+\frac{\partial M_{xy} }{\partial x}. \end{aligned}$$

(A8)