Abstract
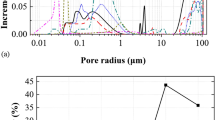
Heating treatment generally causes thermal damage inside rocks, and the influence of thermal damage on mechanical properties of rocks is an important topic in rock mechanics. The coarse marble specimens drilled out from a rock block were first heated to a specific temperature level of 200, 400 and 600 °C except the control group left at 20 °C. A series of triaxial compression tests subjected to the confining pressure of 0, 5, 10, 15, 20, 25, 30, 35 and 40 MPa were conducted. Coupling effects of thermal damage and confining pressure on the mechanical properties of marbles including post-peak behaviors and failure modes, strength and deformation parameters, characteristic stresses in the progressive failure process had been investigated. Meanwhile, accompanied tests of physical properties were carried out to study the effect of thermal damage on microstructure, porosity and P-wave velocity. Finally, the degradation parameter was defined and a strength-degradation model to describe the peak strength was proposed. Physical investigations show that porosity increases slowly and P-wave velocity reduces dramatically, which could be re-demonstrated by the microscopy results. As for the post-peak behaviors and the failure modes, there is a brittle to ductile transition trend with increasing confining pressure and thermal effect reinforces the ductility to some degree. The comparative study on strength and deformation parameters concludes that heating causes damage and confining pressure inhibits the damage to develop. Furthermore, crack damage stress and crack initiation stress increase, while the ratios of crack damage stress to peak strength and crack initiation stress to peak strength show a decreasing trend with the increase of confining pressure; the magnitude of crack damage stress or crack initiation stress shows a tendency of decrease with the increasing heating temperature and the tendency vanishes subjected to high confinement.












Similar content being viewed by others
References
Bahrani N, Kaiser PK (2013) Strength degradation of non-persistently jointed rockmass. Int J Rock Mech Min Sci 62:28–33
Brace WF, Paulding BW, Scholz CH (1966) Dilatancy in the fracture of crystalline rocks. J Geophys Res 71(16):3939–3953
Cai M, Kaiser PK, Tasaka Y, Maejima T, Morioka H, Minami M (2004) Generalized crack initiation and crack damage stress thresholds of brittle rock masses near underground excavations. Int J Rock Mech Min Sci 41(5):833–847
Cantisani E, Pecchioni E, Fratini F, Garzonio CA, Malesani P, Molli G (2009) Thermal stress in the Apuan marbles: relationship between microstructure and petrophysical characteristics. Int J Rock Mech Min Sci 46(1):128–137
Chen YL, Ni J, Shao W, Azzam R (2012) Experimental study on the influence of temperature on the mechanical properties of granite under uni-axial compression and fatigue loading. Int J Rock Mech Min Sci 56:62–66
Eberhardt E, Stead D, Stimpson B, Read RS (1998) Identifying crack initiation and propagation thresholds in brittle rock. Can Geotech J 35(2):222–233
Eberhardt E, Stead D, Stimpson B (1999a) Effects of sample disturbance on the stress-induced microfracturing characteristics of brittle rock. Can Geotech J 36(2):239–250
Eberhardt E, Stimpson B, Stead D (1999b) Effects of grain size on the initiation and propagation thresholds of stress-induced brittle fractures. Rock Mech Rock Eng 32(2):81–99
Emmermann R, Lauterjung J (1997) The German continental deep drilling program KTB: overview and major results. J Geophys Res-Sol Ea (1978–2012) 102(B8):18179–18201
Gónzalez-Gómez WS, Quintana P, May-Pat A, Avilés F, May-Crespo J, Alvarado-Gil JJ (2015) Thermal effects on the physical properties of limestones from the Yucatan Peninsula. Int J Rock Mech Min Sci 75:182–189
Inserra C, Biwa S, Chen Y (2013) Influence of thermal damage on linear and nonlinear acoustic properties of granite. Int J Rock Mech Min Sci 62:96–104
Liu S, Xu J (2014) Mechanical properties of Qinling biotite granite after high temperature treatment. Int J Rock Mech Min Sci 71:188–193
Liu XJ, Gao H, Liang LX (2011) Study of temperature and confining pressure effects on porosity and permeability in low permeability sandstone. Chin J Rock Mech Eng 30:3771–3778
Martin CD, Chandler NA (1994) The progressive fracture of Lac du Bonnet granite. Int J Rock Mech Min Sci Geomech Abstr 31(6):643–659
Martin CD, Christiansson R (2009) Estimating the potential for spalling around a deep nuclear waste repository in crystalline rock. Int J Rock Mech Min Sci 46(2):219–228
Martin CD, Stimpson B (1994) The effect of sample disturbance on laboratory properties of Lac du Bonnet granite. Can Geotech J 31(5):692–702
Nicksiar M, Martin CD (2012) Evaluation of methods for determining crack initiation in compression tests on low-porosity rocks. Rock Mech Rock Eng 45(4):607–617
Nicksiar M, Martin CD (2013) Crack initiation stress in low porosity crystalline and sedimentary rocks. Eng Geol 154:64–76
Peng J, Rong G, Zhou CB (2013) Experimental study of effect of water pressure on progressive failure process of rocks under compression. Rock Soil Mech 34(4):941–946
Peng J, Rong G, Cai M, Wang XJ, Zhou CB (2014) An empirical failure criterion for intact rocks. Rock Mech Rock Eng 47(2):347–356
Pestman BJ, Van Munster JG (1996) An acoustic emission study of damage development and stress-memory effects in sandstone. Int J Rock Mech Min Sci Geomech Abstr 33(6):585–593
Rosengren KJ, Jaeger JC (1968) The mechanical properties of an interlocked low-porosity aggregate. Geotechnique 18(3):317–326
Sun Q, Zhang ZZ, Xue L, Zhu SY (2013) Physico-mechanical properties variation of rock with phase transformation under high temperature. Chin J Rock Mech Eng 32(5):935–942
Tian H, Ziegler M, Kempka T (2014) Physical and mechanical behavior of claystone exposed to temperatures up to 1000 C. Int J Rock Mech Min Sci 70:144–153
Ulusay R, Hudson JA (2007) The complete ISRM suggested methods for rock characterization, testing and monitoring: 1974–2006. ISRM commission on testing methods, Ankata
Xue L, Qin S, Sun Q, Wang Y, Lee LM, Li W (2014) A study on crack damage stress thresholds of different rock types based on uniaxial compression tests. Rock Mech Rock Eng 47(4):1183–1195
Yavuz H, Altindag R, Sarac S, Ugur I, Sengun N (2006) Estimating the index properties of deteriorated carbonate rocks due to freeze–thaw and thermal shock weathering. Int J Rock Mech Min Sci 43(5):767–775
Yavuz H, Demirdag S, Caran S (2010) Thermal effect on the physical properties of carbonate rocks. Int J Rock Mech Min Sci 47(1):94–103
Zhao XG, Cai M, Wang J, Ma LK (2013) Damage stress and acoustic emission characteristics of the Beishan granite. Int J Rock Mech Min Sci 64:258–269
Zhao XG, Cai M, Wang J, Li PF, Ma LK (2015) Objective determination of crack initiation stress of brittle rocks under compression using AE measurement. Rock Mech Rock Eng 48(6):2473–2484
Acknowledgments
The research work presented in this paper is supported by the National Natural Science Foundation of China (Grant No. 51579189), the National Basic Research Program of China (‘‘973’’ Program, Grant No. 2011CB013501), and the Fundamental Research Funds for the Central Universities. The authors are grateful for these financial supports.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Yao, M., Rong, G., Zhou, C. et al. Effects of Thermal Damage and Confining Pressure on the Mechanical Properties of Coarse Marble. Rock Mech Rock Eng 49, 2043–2054 (2016). https://doi.org/10.1007/s00603-016-0916-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00603-016-0916-1