1 Introduction

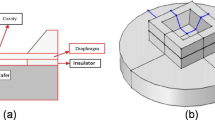
Pressure sensors based upon different transduction techniques including piezoresistive (Mosser et al. 1991; Aryafar et al. 2015; Shaby et al. 2015; Rajavelu et al. 2014) (using the change in the resistance to detect strain in diaphragm-embedded strain gauges due to applied pressure), capacitive (Palasagaram and Ramadoss 2006; Rochus et al. 2016; Molla-Alipour and Ganji 2015; Sundararajan and Hasan 2014; Lei et al. 2012) (using the diaphragm deflection due to applied pressure/or pressure difference in the cavity to create a variable capacitor), resonance (Petersen et al. 1991; Burns et al. 1994; Burns et al. 1995) (measuring the change in resonance frequency of edge clamped plate/bridge due to the applied pressure), piezoelectric (Eaton and Smith 1997; Koal 1985; Sharma et al. 2012) (measuring the influence of the pressure on the charge in certain materials, such as quartz, III–V compound semiconductors and others), optical (Wagner et al. 1993; Dziuban et al. 1992; Wagner et al. 1994) (using Mach–Zehnder interferometry for measuring pressure induced deflection) and thermal (Haberli et al. 1996) (measuring the heat transfer across an air gap between source and sink based upon applied pressure) have been developed. Among these, most of the pressure sensor designs incorporate a membrane or diaphragm (as depicted in Fig. 1), whose mechanical deflection stimulates the transduction.

Fig. 1
figure 1

Optical micrograph (top-view) of a diaphragm based MEMS piezoresistive pressure sensor. The sensor has four piezoresistors embedded in the diaphragm (transparent membrane) to detect pressure as a function of membrane deflection

Full size image

Membrane or diaphragm-based micro-fabricated pressure sensors are used in the medical, aerospace, process control, automation and automotive industries (Bogue 2007). Although, the very first diaphragm pressure sensor and strain gauge were reported in 1958 (Bryzek et al. 1990) and their full scale commercialization was achieved in 1990 (Bryzek 2012), yet the efforts to further improve the micro-fabricated pressure sensors’ mechanical design (and hence performance) by optimizing its shape/geometrical parameters still continue. For example, the effect of diaphragm thickness and side length on sensitivity and resonant frequency were studied and it was concluded that both the sensor diaphragm and side length need to be reduced to achieve a pressure-sensitive diaphragm with high resonance frequency (Wang et al. 2006). Similarly, geometric optimization of a piezoresistive pressure sensor with measurement span of 1 MPa was also carried out for enhanced sensitivity and linearity (Ferreira et al. 2012). In this case, optimization was carried out by varying membrane thickness, edge length to thickness ratio and optimal positioning of the piezoresistive sensing elements. In another study, the effects of membrane or diaphragm thickness and edge length on pressure sensor’s sensitivity were explored and a perforated membrane was proposed for improved sensitivity (Rajavelu et al. 2014). Thermal and packaging effects on the sensitivity and stability of a silicon based piezoresistive pressure sensor, caused by the geometry of silicon gel (which was used to protect the die surface) were also studied (Chou et al. 2009).

Most of the past attempts to improve the mechanical design and performance of micro-fabricated pressure sensors are primarily focused on shape or geometry optimization, and not much attention has been given to optimization of its materials. The only exceptions are papers by Spearing et al. (2000) and Qian and Zhao (2002), which report the material aspects of the mechanical design of MEMS pressure sensors. However, the data set of the materials considered in these studies was very small. Only a total of eight and nine materials were included in their studies, respectively, and material properties considered for optimization were compared in a tabular form, mainly due to non-availability of a comprehensive MEMS materials database. Furthermore, the candidate materials for simultaneously maximizing both the key performance parameters (i.e. diaphragm deflection and resonance frequency) have never been explored or reported in the past. Maximizing both these performance requirements simultaneously is a case of conflict between the two mechanical design objectives as the material’s Young’s modulus is required to be maximized for achieving maximum natural frequency whereas, it is required to be minimized for achieving maximum diaphragm deflection.

In this paper, therefore, first a sizeable micro-scale properties data of MEMS materials has been consolidated. Subsequently, this data has been used along with a material selection software. Following Ashby’s material selection approach (Ashby 1989; Ashby and Cebon 1993; Ashby et al. 2004; Ashby 2005), the Performance and Material Indices have been developed for a more demanding and conflicting mechanical design requirements of a MEMS pressure sensor diaphragm. In conjunction with the derived Performance and Material Indices, the consolidated materials data has been then utilized to select materials for maximizing MEMS pressure sensor diaphragm deflection and natural frequency, simultaneously. For the sake of comparison, material selection for maximizing MEMS pressure sensor diaphragm deflection and its natural resonance frequency separately has also been performed.

The structure of the remaining paper is as follows. Section 2 presents the consolidation process of MEMS materials data and its integration with the Cambridge Engineering Selector (CES) material selection software. Section 3 briefly reviews Ashby’s material selection approach. Derivation of performance indices for conflicting requirements of MEMS pressure sensor diaphragm design is presented in Sect. 4. Material selection charts and candidate materials for three considered cases (i.e. maximizing only diaphragm deflection, maximizing only diaphragm resonance frequency and maximizing both diaphragm deflection and frequency simultaneously) are presented in Sect. 5. Finally, concluding remarks are given in Sect. 6.

2 MEMS materials data

A data set of micro-scale properties for MEMS materials falling in three classes i.e. (a) ceramics, (b) metals and (c) polymers, has been consolidated in Tables 1, 2, and 3, respectively. Three material properties (i.e. density, Young’s modulus, and ultimate tensile strength), which are most pertinent to our study have been included in the data. For most of the MEMS materials, their properties have been reported by more than one researcher, e.g. silicon as MEMS material has been reported by 10 different researchers. Interestingly, the material properties (specifically ultimate tensile strength) of many MEMS materials vary in different papers; e.g. ultimate tensile strength of silicon by three researchers has been reported as 4000 MPa, whereas the other two reported it as 1000 MPa (ref Table 1). In such cases, where possible, ultimate tensile strength data was traced back to the specific test results. The material properties used in our data are then either taken from the reported micro-fabricated structures or from the recommended initial design values in the literature, based upon the variety of material characterization techniques. In some cases these are backed by our own experience with designing and characterization of MEMS structures.

Table 1 MEMS/micro-scale material properties: ceramics
Full size table
Table 2 MEMS/micro-scale material properties: metals and alloys
Full size table
Table 3 MEMS/micro-scale material properties: polymers
Full size table

The material properties data collected in respect of these MEMS materials was then integrated with Cambridge Engineering Selector (CES), a software developed by Granta Design (Cambridge Engineering Selector (CES), Software 1999), which is a comprehensive material selection software (Ramalhete et al. 2010).

3 Ashby’s material selection methodology

In Ashby’s methodology (Ashby 1989, 2005; Ashby and Cebon 1993; Ashby et al. 2004), the performance of a structural element is determined by three parameters: (1) the functional requirements, (2) the geometry and (3) the properties of the material of which it is made. The performance P of the element is described by an equation in the form of a product as:

$$P = \left[ {\left( {\begin{array}{*{20}c} {Function } \\ {requirements, F} \\ \end{array} } \right) \times \left( {\begin{array}{*{20}c} {Geometric} \\ { requirement, G} \\ \end{array} } \right) \times \left( {\begin{array}{*{20}c} {Material } \\ {requirement, M} \\ \end{array} } \right)} \right]$$
(1)

The three parameters in Eq. (1) are independent and separable, which implies that the material requirement portion of this equation can be solved independently without solving the complete design problem or even knowing about the complete details of F and G. Therefore, from formulated performance indices (Eq. 1 above), material indices are extracted and based upon these, material selection charts are generated. The x-axis and y-axis of these material selection charts are the material properties that are aimed to be optimized. Available materials are plotted on these charts and the materials best fulfilling the selection criteria are chosen. Due to usefulness of Ashby’s material selection strategy, it has not only been widely adopted in material selection for general applications and macro-systems e.g. (Ashby 1989, 2000; Ashby and Cebon 1993; Wood et al. 1997; Cebon and Ashby 1994; Huber et al. 1997) but also for a number of Microsystems/MEMS (with limited MEMS material data sets) e.g. (Sharma et al. 2012; Spearing 2000; Qian and Zhao 2002; Prasanna and Spearing 2007; Srikar and Spearing 2003a, b; Srinivasan and Spearing 2008; Pratap and Arunkumar 2007; Guisbiers et al. 2007, 2010; Guisbiers and Wautelet 2007; Reddy and Gupta 2010; Sharma and Gupta 2012; Mehmood et al. 2018).

4 Performance indices for conflicting design requirements of MEMS pressure sensor diaphragm

The main structural element of a micro-fabricated pressure sensor is its diaphragm. Such diaphragms are normally circular (Jeong 2015; Yasukawa et al. 1982) or square (Kumar and Pant 2015, 2016) (Fig. 2). In terms of shape, it is well established that for two different pressure sensors with diaphragm made of any material having same thickness and same side length or diameter, the one with square shape will experience 1.64 times higher stresses compared to the one having a circular diaphragm (Berns et al. 2006) for same applied pressure. However, material choice becomes independent of the diaphragm shape when presented in the form of Eq. (1) above. Therefore, in the current design study, we focus only on selection and optimization of the material of a pressure sensor diaphragm (and not its shape) for a more demanding and conflicting requirement of simultaneous maximization of both the diaphragm deflection and resonance frequency. The Performance Index for individual maximization of the diaphragm deflection is given as \(M_{1} = \frac{{\sigma_{f}^{3/2} }}{E}\), while that for maximization of the resonance frequency alone is reported as \(M_{2} = \sqrt {\frac{E}{\rho }}\) (Spearing 2000; Qian and Zhao 2002). In these Performance Indices, ‘\(E\)’ is the material’s Young’s modulus, ‘\(\rho\)’ is the mass density and ‘\(\sigma_{f}\)’ is the ultimate tensile strength, which is taken as the ultimate tensile strength of the material for all practical engineering applications.

Fig. 2
figure 2

Typical geometry of a MEMS pressure sensor’s circular and square diaphragms where \(a\) is the diaphragm’s diameter (for circular membrane)/side length (for square membrane), h is the diaphragm thickness and \(\delta_{\hbox{max} }\) is the maximum diaphragm deflection

Full size image

In order to maximize M1 index, the requirement is to select the material with maximum value of ‘\(\sigma_{f}\)’ and minimum value of ‘\(E\)’, where as for maximizing the index M2, it is required that a material with maximum value of ‘\(E\)’ is selected, which is contradictory to the requirement of M1. To handle these conflicting requirements, a systematic procedure has been adopted (Ashby 2005). First, the relevant performance indices have been normalized by dividing the individual index by the properties of any one selected reference/standard material (silicon in our case whose Young’s modulus, ultimate tensile strength and density are denoted by \(E_{0}\), \(\sigma_{{f_{0} }}\) and \(\rho_{0}\), respectively). After normalizing the indices, the problem can then be converted to the problem of minimization. The normalization of the index M1 is given by Eq. (2) and for converting it into a minimization problem, its reciprocal is taken which is given by Eq. (3). Similarly, normalization and minimization of material index M2 are given by Eqs. (4) and (5).

$$\frac{{M_{1} }}{{M_{1,0} }} = \frac{{\sigma_{f}^{{^{3/2} }} }}{{\sigma_{{f_{0} }}^{3/2} }}\frac{{E_{0} }}{E}$$
(2)
$$\frac{{M_{1,0} }}{{M_{1} }} = \frac{{\sigma_{{f_{0} }}^{3/2} }}{{\sigma_{f}^{3/2} }}\frac{E}{{E_{0} }}$$
(3)
$$\frac{{M_{2} }}{{M_{2,0} }} = \sqrt {\frac{{E \, \rho_{0} }}{{E_{0} \, \rho }}}$$
(4)
$$\frac{{M_{2,0} }}{{M_{2} }} = \sqrt {\frac{{E_{0} \, \rho }}{{E \, \rho_{0} }}}$$
(5)

5 Material selection charts and candidate materials

Based upon the derived Performance Indices for the conflicting requirements of a MEMS pressure sensor’s diaphragm design, material selection charts have been developed. Material properties of MEMS materials included in our MEMS materials data-base have been utilized to plot these charts. Log–log scale was used to cover the wide range of the data. Three different material selection charts with respect to three different design criteria, presented below, have been developed. Candidate materials for a variety of applications, using each design criterion, have also been elaborated.

5.1 Case 1: maximizing diaphragm deflection

The Performance Index governing the diaphragm deflection is given (Spearing 2000; Qian and Zhao 2002) as:

$$M_{1} = {\raise0.7ex\hbox{${\sigma _{f}^{{3/2}} }$} \!\mathord{\left/ {\vphantom {{\sigma _{f}^{{3/2}} } E}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$E$}}$$
(6)

In order to achieve maximum diaphragm deflection without failure, materials with maximum value of ‘\(\sigma_{f}\)’ and minimum value of ‘\(E\)’ are required. Figure 3 is the plot of failure strength (ultimate tensile strength) ‘\(\sigma_{f}\)’ shown on the y-axis and Young’s modulus ‘\(E\)’ depicted on the x-axis. Grid lines with slope = 2/3 (by taking log of material index M1 we get the slope of line as 2/3) were plotted on the chart. On each grid line \({\raise0.7ex\hbox{${\sigma _{f} }$} \!\mathord{\left/ {\vphantom {{\sigma _{f} } E}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$E$}}\) has the same value; above each grid line \({\raise0.7ex\hbox{${\sigma _{f} }$} \!\mathord{\left/ {\vphantom {{\sigma _{f} } E}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$E$}}\) has higher values, while below the grid line it has lower values.

Fig. 3
figure 3

MEMS pressure sensor diaphragm material selection chart for maximizing diaphragm deflection

Full size image

It is evident from Fig. 3 that ceramics and polymers are promising materials for maximizing diaphragm deflection, whereas metals are comparatively less attractive. Among the ceramics silicon with crystal orientation 110 [i.e. (Si (110)] is top ranked, while from the polymers Poly-Di-Methyl-Siloxane (PDMS) and silicone rubber are the most suitable materials for applications requiring maximum deflection of pressure sensor diaphragm.

The conventionally used membrane material from ceramics i.e. Si (100) and polysilicon (Poly-Si) fall at second tier of the candidate materials identified in Fig. 3. Other ceramics materials comparable with Si (100) are silicon nitride (SiN), germanium (Ge), 3H silicon carbide (3H-SiC), diamond and Diamond Like Carbon (DLC). As such there are no MEMS devices reported in the literature that uses 3H-SiC, however few devices made of Ge have been reported but mostly for optoelectronics applications (Burt et al. 2017; Scopece et al. 2014). MEMS devices made of SiN, diamond and DLC and incorporating membranes for their applications are reported in the literature. However, these have been used for specific applications, details of which have been discussed in the next sections.

Similarly, polymers such as Poly-Vinyli-Dene-Fluoride (PVDF), Poly-Methyl-Meth-Acrylate) (PMMA), parylene, Polyaniline (PANI) and Polypyrrole (PPy) also fall in the second tier of the candidate materials after PDMS and silicone rubber. On the other hand, SU-8 and polyimide emerged as far inferior in terms of maximizing diaphragm deflection. Polyaniline (PANI) is suitable for gas sensing applications and its use to sense different gases has been demonstrated (Liu et al. 2009; Lee et al. 2005). Polypyrrole (PPy) is a low cost environmental friendly material that has been mainly used as an electrode material in super capacitors (Sun and Chen 2009; Sun et al. 2010; Beidaghi and Wang 2011). However, PVDF and PMMA have been used to fabricate the pressure sensor in the past. Both PVDF and PMMA have an added advantage of being bio-compatible (Fung et al. 2005a, b; Shirinov and Schomburg 2008). Because of their low Young’s modulus, they have a higher sensitivity compared to conventionally used Si (100); however, their pressure range is limited.

Among all these materials, the three materials i.e. Si(110), PDMS and silicone rubber that lie along the same line on the materials selection chart (i.e. green line, Fig. 3), emerge as most suitable materials since they have the same value of index M1. However, the final choice of the diaphragm material would depend upon the required pressure range and sensitivity of the pressure sensor.

Owing to higher values of Young’s modulus, amongst the ceramics, Si (110) appears as one of the most suitable material for applications requiring measurement of higher pressures with a wider range. From micro-machining point of view, Si(110) is a CMOS compatible material and has a higher etch rate in alkali-based etchant than the conventionally used Si(100). Moreover, Si(110) surface intersects the four (111) planes at right angle, making it a suitable material for achieving structures with perfectly vertical walls (Ghodssi and Lin 2011; Lee et al. 1999), whereas such structures are not possible to achieve with Si(100) wafer using any wet etchant.

Among polymers, small stiffness values of PDMS and silicone rubber suggest them to be suitable for high sensitivity applications. Using MEMS fabrication process, membranes of silicone rubber and PDMS have been realized (Lee and Choi 2008; Yang et al. 1999).

Silicone rubber is IC compatible and exhibits excellent adhesion with CMOS compatible materials such as silicon, silicon nitride and silicon oxide. However, silicone rubber undergoes plastic deformation even with the application of small pressure (Yang et al. 1999). Moreover, its properties tend to be highly temperature dependent, which makes it very difficult to work with as a sensor (Rey et al. 2013).

PDMS, a polymer material well known for its biocompatibility and low cost, is widely used for MEMS applications. Its usage as a membrane material in biocompatible pressure sensors has also been widely demonstrated (Lee and Choi 2008; Liu et al. 2013; Kim and Meng 2015; Zhou et al. 2018; Xue et al. 2018; Peng et al. 2018; Chaudhury et al. 2016). One such study by Lee and Choi (2008) reported fabrication of a PDMS diaphragm pressure sensor and compared its deflection versus applied pressure curve with that of a conventional silicon [Si(100)] diaphragm pressure sensor. For the same amount of applied pressure, PDMS diaphragm underwent higher deflection than the conventional Si(100) diaphragm pressure sensor. The higher deflection of PDMS diaphragm resulted into higher sensitivity compared with the Si(100) diaphragm pressure sensor. Nevertheless, for PDMS, high volume manufacturability, long term reliability and mass production cost remain challenges to be considered, when compared to silicon.

5.2 Case 2: maximizing diaphragm resonance frequency (minimizing resonance time constant)

The Performance Index governing the resonance frequency of pressure sensor diaphragm (Spearing 2000; Qian and Zhao 2002) is M2 =  \(\sqrt {{\raise0.7ex\hbox{$E$} \!\mathord{\left/ {\vphantom {E \rho }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\rho $}}}\). To achieve maximum frequency of vibration, materials with maximum value of ‘\(E\)’ and minimum value of ‘\(\rho\)’ are required. Figure 4 is the plot of the two material properties (i.e. ‘\(E\)’ on the y-axis and ‘\(\rho\)’ on x-axis). Grid lines with slope = 1 were plotted on the chart. On each grid line,\({\raise0.7ex\hbox{$E$} \!\mathord{\left/ {\vphantom {E \rho }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\rho $}}\) (specific stiffness) has a constant value, the top most grid line has the highest value of \({\raise0.7ex\hbox{$E$} \!\mathord{\left/ {\vphantom {E \rho }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\rho $}}\), while decreases on lower lines with the one at bottom having the lowest value.

Fig. 4
figure 4

MEMS pressure sensor diaphragm material selection chart for maximizing diaphragm resonance frequency (or minimizing vibration time constant)

Full size image

It is evident from Fig. 4 that only ceramics are promising materials for maximizing diaphragm resonance frequency, whereas metals and polymers are comparatively less attractive. Among the ceramics, diamond, Diamond Like Carbon (DLC) and Ultra Nano Crystalline Diamond (UNCD) are the preferred materials for pressure sensor diaphragm intended to be used for high frequency pressure measurement applications.

At the second tier of Fig. 4, materials such as silicon carbide (SiC), 3H-SiC, SiN and aluminum oxide (AlO) also appear as potential candidate materials for high frequency applications. Aluminum oxide is mainly being used as a humidity sensor (Lan et al. 2018; Kim et al. 2009; Nahar 2000); however, due to its high specific stiffness (\({\raise0.7ex\hbox{$E$} \!\mathord{\left/ {\vphantom {E \rho }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\rho $}}\)) it can potentially be used for high frequency applications as well (Spearing 2000). Similar to aluminum oxide, SiC also has high specific stiffness. Additionally, it also has high thermal conductivity, high electric field breakdown strength and wide band-gap, making it a good candidate material for high temperature, high power and high frequency applications (Casady and Johnson 1996). To exploit all these advantages, SiC pressure sensors have been developed for applications in harsh environment (Wieczorek et al. 2007; Beker et al. 2017).

Figure 4 also depicts that diamond, Diamond Like Carbon (DLC) and Ultra Nano Crystalline Diamond (UNCD) are even better than silicon carbide for high frequency applications.

Diamond and DLC can be deposited in the form of thin films using a variety of deposition techniques such as plasma enhanced chemical vapor deposition, plasma assisted chemical vapor deposition, microwave plasma chemical vapor deposition, ion beam deposition, pulsed laser ablations, filtered cathodic arc deposition, magnetron sputtering and DC plasma-jet chemical vapor deposition (Boudina et al. 1992; Fu et al. 2000; Santra et al. 2012). Though the deposition of diamond and DLC include some inherent issues such as high deposition temperature (600–1000 °C), large intrinsic and thermal stresses, low deposition rates, poor adhesion to substrate and higher values of surface roughness (Luo et al. 2007), yet the use of diamond in high frequency applications (Baliga 1989; Taniuchi et al. 2001) and realization of its membranes has been demonstrated (Davidson et al. 1999; Kohn et al. 1999). Pressure sensors made of all diamond (i.e. both membranes and piezoresistors are made of diamond) have also been fabricated and characterized (Wur et al. 1995; Davidson et al. 1996).

In spite of successful demonstration of diamond and DLC in high frequency measurement applications, their deposition related issues restrict the exploitation of full benefits of diamond and DLC in wider MEMS applications. Many of these issues were however, resolved in UNCD film technology developed by Argonne National Laboratory (Auciello et al. 2004), rendering UNCD also a promising MEMS materials for high frequency applications. The developed UNCD films have been successfully implemented to form wide dynamic range pressure, acceleration and vibration sensors (Krauss et al. 2002).

5.3 Case 3: simultaneous maximization of diaphragm deflection and vibration frequency

The material selection chart for selecting optimized materials considering both the design requirements (i.e. maximum deflection and maximum frequency) of MEMS pressure sensor diaphragm is given in Fig. 5. In this figure, Eq. (3) has been plotted on the y-axis, while Eq. (5) is on the x-axis. Figure 5 has been divided into four sectors, with point (1,1) corresponding to silicon being in the center, which has been selected as reference material for comparison. The materials falling in sector A are the best materials having both the performance parameters (i.e. deflection and frequency) at maximum and superior to silicon. Materials falling in sector B, C and D have performance, in terms of both deflection and frequency, inferior to that of silicon with materials in sector C being the least promising.

Fig. 5
figure 5

MEMS pressure sensor diaphragm material selection chart for simultaneously maximization of both the diaphragm deflection and its vibration frequency

Full size image

Figure 5 reveals that when both diaphragm deflection and its resonance frequency are required to be maximized simultaneously, then ceramics are the most promising candidate materials, while metals and polymers are far inferior to ceramics. Figure 5 also reveals that 3H-SiC, silicon nitride (SiN) and (110) oriented silicon [i.e. Si(110)] are the only three materials, which would perform better than most frequently reported silicon diaphragm based MEMS pressure sensors.

Interestingly, UNCD (that previously emerged as the most suitable material for high frequency applications of pressure sensor) and PDMS (which previously emerged as the most suitable material for large deflection applications of pressure sensor) have inferior performance, when both diaphragm deflection and frequency are required to be maximized simultaneously. However, Si (110), which emerged as the most suitable material for applications requiring large deflections, is still a candidate material for maximizing both deflection and frequency simultaneously. The other preferred material in this case is silicon nitride. 3H-SiC is also depicted to be a promising material in this case. However, as mentioned earlier, no 3H-SiC based MEMS devices have yet been reported.

While both Si(110) and SiN are CMOS compatible materials, Si(110) has a number of unique advantages: (a) it is mechanically superior than Si (100), (b) it has higher etch rate in Alkali-based etchant than the conventionally used Si (100), (c) its surface intersects the four (111) planes at right angle making it a suitable material for achieving structures with perfectly vertical walls (Ghodssi and Lin 2011; Lee et al. 1999), (d) the maximum longitudinal piezoresistance coefficient is along <111> direction, which is on silicon (110) plane. Kanda et al. (Kanda and Yasukawa 1997) showed that when the non-linearity and the full scale pressure are the same, the sensitivity of a piezoresistor pressure sensor on Si(110) wafer is 1.4 times higher than that of the conventionally used Si(100) wafer. The only disadvantage associated with Si (110) oriented wafer is that rectangular-bottom cavities cannot be achieved using wet etchant as two of (111) planes intersect Si(110) plane perpendicularly at an angle of 109.48° and remaining two intersect Si(110) plane surface at an angle of 35.26° (Bassous 1978). However, this limitation has been overcome by using more advanced etching techniques such as deep reactive ion etching (DRIE). This has been demonstrated experimentally by Lee et al. (Lee et al. 2009) whereby 100 µm tall vertical mirrors were fabricated using a combination of KOH etch and DRIE.

The findings of our current study and the past literature (Kanda and Yasukawa 1997) suggest that Si(110) has a good potential to increase the sensitivity of a diaphragm pressure sensor, which has yet not been exploited. It is worth mentioning that Si(110) is an active research area (Rao et al. 2017; Dutta et al. 2011; Hölke and Henderson 1999; Singh et al. 2017; Swarnalatha et al. 2018) and already being used for fabrication of various micro-machined/MEMS devices. Examples of Si(110) wafer based micro-machined devices include a high aspect ratio comb actuator (Kim et al. 2002), a high sensitivity vertical hall sensor (Chiu et al. 2001), a capacitive accelerometer for air bag application (Tsugai et al. 1997), an opto-mechanical accelerometer based on strain sensing by a Bragg grating in a planar waveguide (Storgaard-Larsen et al. 1996), a vertical-membrane optical-fiber pressure sensor (Tu and Zemel 1993), a micro-channel (Singh et al. 2008) and an optical Fabry–Perot modulator (Chaffey et al. 2004) etc.

On the other hand, pressure sensors having silicon nitride (SiN) membranes have also been demonstrated (Kumar and Pant 2015). Using silicon nitride as a membrane material is advantageous in a sense that it has a higher strength than the conventionally used Si(100) membrane. Folkmer et al. (Folkmer et al. 1996) conducted a blister test on membranes made of conventional silicon, silicon carbide and silicon nitride. They demonstrated that silicon nitride membrane has the highest strength (maximum pressure taking capability). However, random crystalline orientation, smaller crystalline grain size and presence of high residual stresses in the SiN are the issues (Eaton et al. 1999; Sugiyama et al. 1986) to be catered while using it as diaphragm material in pressure sensors.

6 Conclusions

Material selection for MEMS based pressure sensor, taking into account the demanding and conflicting requirement of simultaneously maximizing its diaphragm deflection and natural frequency of vibration, has been reported for the first time. Since no comprehensive MEMS materials database incorporating micro-scale properties was readily available, first a MEMS specific materials data is consolidated, which included three key properties (i.e. density, Young’s modulus and ultimate tensile strength) at micro-scale for ceramics (Table 1), metals and alloys (Table 2) and polymers (Table 3) reported in the literature. This data has been then successfully integrated with a material selection software, CES (Cambridge Engineering Selector), to develop material selection charts.

Based upon the formulated Performance Indices, the performance of MEMS materials included in the consolidated MEMS micro-scale properties data has been analyzed for three different design requirements of pressure sensor. The materials, which emerge as the most suitable materials for these design requirements are further critically analyzed in light of microfabrication processes available for them. Amongst the candidate materials whose microfabrication or application in micro-sensors has been previously demonstrated, the most promising materials have been identified for the three design conditions requirements in this study.

Our analysis suggests that PDMS is a promising material to be used for pressure sensor diaphragms requiring large deflection, high sensitivity as well as bio-compatibility. If the aim is to achieve only a high frequency response, then UNCD is the best material. Silicon with crystal orientation 110 [i.e. Si(110)] emerged as most suited material capable of fulfilling two distinct design requirement of MEMS pressure sensor diaphragms: (a) for pressure sensors requiring only maximum diaphragm deflection (and sensitivity) for measurement of high pressures over wide pressure ranges. (b) for simultaneously achieving highest deflection (sensitivity) and highest frequency response of diaphragm. This is in close agreement with the fact highlighted previously that the performance of conventional silicon pressure sensor can be increased by a factor of 1.4 if Si(100) diaphragm is replaced with the Si(110) diaphragm.

This study has hence identified an opportunity for MEMS designers and researchers to exploit the Si(110) diaphragm based pressure sensors for achieving improved pressure measurement range, higher frequency and higher sensitivity compared to the Si(100) based MEMS pressure sensors.

The material selection methodology and the MEMS materials data with micro-scale material properties reported in this design case study is not only limited for selection of materials for MEMS pressure sensors but can also be applied for systematic and successful material selection of other MEMS devices.