Discrete boundary element methods on general meshes in 3D

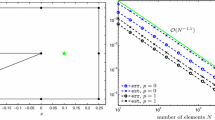
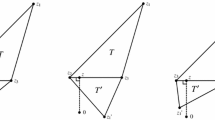
Abstract. This paper is concerned with the stability and convergence of fully discrete Galerkin methods for boundary integral equations on bounded piecewise smooth surfaces in $\mathbb{R}^3$. Our theory covers equations with very general operators, provided the associated weak form is bounded and elliptic on $H^\mu$, for some $\mu \in [-1,1]$. In contrast to other studies on this topic, we do not assume our meshes to be quasiuniform, and therefore the analysis admits locally refined meshes. To achieve such generality, standard inverse estimates for the quasiuniform case are replaced by appropriate generalised estimates which hold even in the locally refined case. Since the approximation of singular integrals on or near the diagonal of the Galerkin matrix has been well-analysed previously, this paper deals only with errors in the integration of the nearly singular and smooth Galerkin integrals which comprise the dominant part of the matrix. Our results show how accurate the quadrature rules must be in order that the resulting discrete Galerkin method enjoys the same stability properties and convergence rates as the true Galerkin method. Although this study considers only continuous piecewise linear basis functions on triangles, our approach is not restricted in principle to this case. As an example, the theory is applied here to conventional “triangle-based” quadrature rules which are commonly used in practice. A subsequent paper [14] introduces a new and much more efficient “node-based” approach and analyses it using the results of the present paper.