Negative norm error control for second-kind convolution Volterra equations

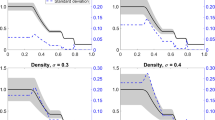
Summary. We consider a piecewise constant finite element approximation to the convolution Volterra equation problem of the second kind: find $u$ such that $u = f + \phi * u$ in a time interval $[0,T]$. An a posteriori estimate of the error measured in the $W^{-1}_p(0,T)$ norm is developed and used to provide a time step selection criterion for an adaptive solution algorithm. Numerical examples are given for problems in which $\phi$ is of a form typical in viscoelasticity theory.