Abstract
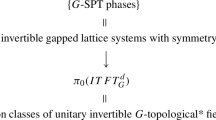
It has been proposed recently that interacting Symmetry Protected Topological Phases can be classified using cobordism theory. We test this proposal in the case of Fermionic SPT phases with \( {\mathrm{\mathbb{Z}}}_2 \) symmetry, where \( {\mathrm{\mathbb{Z}}}_2 \) is either time-reversal or an internal symmetry. We find that cobordism classification correctly describes all known Fermionic SPT phases in space dimension D ≤ 3 and also predicts that all such phases can be realized by free fermions. In higher dimensions we predict the existence of inherently interacting fermionic SPT phases.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
S. Ryu, A.P. Schnyder, A. Furusaki and A.W.W. Ludwig, Topological insulators and superconductors: Tenfold way and dimensional hierarchy, New J. Phys. 12 (2010) 065010 [INSPIRE].
A. Kitaev, Periodic table for topological insulators and superconductors, AIP Conf. Proc. 1134 (2009) 22 [arXiv:0901.2686] [INSPIRE].
L. Fidkowski and A. Kitaev, Topological phases of fermions in one dimension, Phys. Rev. B 83 (2011) 075103 [arXiv:1008.4138].
C. Wang and T. Senthil, Interacting fermionic topological insulators/superconductors in three dimensions, Phys. Rev. B 89 (2014) 195124 [arXiv:1401.1142] [INSPIRE].
Z.C. Gu and M. Levin, The effect of interactions on 2D fermionic symmetry protected topological phases with Z 2 symmetry, Phys. Rev. B 89 (2014) 201113 [arXiv:1304.4569].
X. Chen, Z.-C. Gu, Z.-X. Liu and X.-G. Wen, Symmetry protected topological orders and the group cohomology of their symmetry group, Phys. Rev. B 87 (2013) 155114 [arXiv:1106.4772] [INSPIRE].
Z.-C. Gu and X.-G. Wen, Symmetry-protected topological orders for interacting fermions: fermionic topological nonlinear σ models and a special group supercohomology theory, Phys. Rev. B 90 (2014) 115141 [arXiv:1201.2648] [INSPIRE].
L. Fidkowski, X. Chen and A. Vishwanath, Non-abelian topological order on the surface of a 3D topological superconductor from an exactly solved model, Phys. Rev. X 3 (2013) 041016.
A. Kapustin, Symmetry protected topological phases, anomalies and cobordisms: beyond group cohomology, arXiv:1403.1467 [INSPIRE].
A. Kapustin, Bosonic topological insulators and paramagnets: a view from cobordisms, arXiv:1404.6659 [INSPIRE].
D. Cimasoni and N. Reshetikhin, Dimers on surface graphs and spin structures. I, Comm. Math. Phys. 275 (2007) 187 [math-ph/0608070].
N. Read and D. Green, Paired states of fermions in two-dimensions with breaking of parity and time reversal symmetries and the fractional quantum Hall effect, Phys. Rev. B 61 (2000) 10267 [cond-mat/9906453] [INSPIRE].
J. Milnor and J Stasheff, Characteristic classes, Princeton University Press, Princeton U.S.A. (1974).
R.C. Kirby and L.R. Taylor, Pin structures on low dimensional manifolds.
X. Chen, Y-M. Li and A. Vishwanath, Symmetry protected topological phases from decorated domain walls, Nature Commun. 5 (2014) 3507 [arXiv:1303.4301].
D.W. Anderson, E.H. Brown Jr. and F.P. Peterson, The structure of the Spin cobordism ring, Ann. Math. 86 (1967) 271.
D.W. Anderson et al., Pin cobordism and related topics, Comment. Math. Helv. 44 (1969) 462.
R. Kirby and L. Taylor, A calculation of Pin + bordism groups, Comment. Math. Helv. 65 (1990) 434.
E. Barrera-Yanez, The moduli space \( \mathrm{\mathcal{M}}(M) \) of certain non-orientable manifolds of even dimension.
E.H. Brown Jr., Generalizations of the Kervaire Invariant, Ann. Math. 95 (1972) 368.
S. Stolz, Exotic structures on 4-manifolds detected by spectral invariants, Inv. Math. 94 (1988) 147.
R. Blumenhagen, D. Lüst and S. Theisen, Basic concepts of string theory, Springer Germany (2013).
Open Access
This article is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
ArXiv ePrint: 1406.7329
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kapustin, A., Thorngren, R., Turzillo, A. et al. Fermionic symmetry protected topological phases and cobordisms. J. High Energ. Phys. 2015, 1–21 (2015). https://doi.org/10.1007/JHEP12(2015)052
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/JHEP12(2015)052