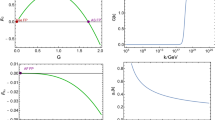
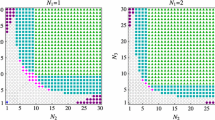
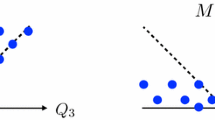
Abstract
We study the ultraviolet behaviour of four-dimensional quantum field theories involving non-abelian gauge fields, fermions and scalars in the Veneziano limit. In a regime where asymptotic freedom is lost, we explain how the three types of fields cooperate to develop fully interacting ultraviolet fixed points, strictly controlled by perturbation theory. Extensions towards strong coupling and beyond the large-N limit are discussed.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
K.G. Wilson, Renormalization group and critical phenomena. 1. Renormalization group and the Kadanoff scaling picture, Phys. Rev. B 4 (1971) 3174 [INSPIRE].
K.G. Wilson, Renormalization group and critical phenomena. 2. Phase space cell analysis of critical behavior, Phys. Rev. B 4 (1971) 3184 [INSPIRE].
D.J. Gross and F. Wilczek, Ultraviolet behavior of non-Abelian gauge theories, Phys. Rev. Lett. 30 (1973) 1343 [INSPIRE].
H.D. Politzer, Reliable perturbative results for strong interactions?, Phys. Rev. Lett. 30 (1973) 1346 [INSPIRE].
D.J.E. Callaway, Triviality pursuit: can elementary scalar particles exist?, Phys. Rept. 167 (1988) 241 [INSPIRE].
S. Weinberg, Ultraviolet divergences in quantum theories of gravitation, in General relativity: an Einstein centenary survey, S.W. Hawking and W. Israel eds., (1979), pg. 790 [INSPIRE].
D.F. Litim, Renormalisation group and the Planck scale, Phil. Trans. Roy. Soc. Lond. A 369 (2011) 2759 [arXiv:1102.4624] [INSPIRE].
D.F. Litim, On fixed points of quantum gravity, AIP Conf. Proc. 841 (2006) 322 [hep-th/0606044] [INSPIRE].
M. Niedermaier, The asymptotic safety scenario in quantum gravity: an introduction, Class. Quant. Grav. 24 (2007) R171 [gr-qc/0610018] [INSPIRE].
M. Niedermaier and M. Reuter, The asymptotic safety scenario in quantum gravity, Living Rev. Rel. 9 (2006) 5 [INSPIRE].
R. Percacci, Asymptotic safety, arXiv:0709.3851 [INSPIRE].
D.F. Litim, Fixed points of quantum gravity and the renormalisation group, PoS(QG-Ph)024 [arXiv:0810.3675] [INSPIRE].
M. Reuter and F. Saueressig, Quantum Einstein gravity, New J. Phys. 14 (2012) 055022 [arXiv:1202.2274] [INSPIRE].
D.I. Kazakov, Ultraviolet fixed points in gauge and SUSY field theories in extra dimensions, JHEP 03 (2003) 020 [hep-th/0209100] [INSPIRE].
H. Gies, J. Jaeckel and C. Wetterich, Towards a renormalizable standard model without fundamental Higgs scalar, Phys. Rev. D 69 (2004) 105008 [hep-ph/0312034] [INSPIRE].
T.R. Morris, Renormalizable extra-dimensional models, JHEP 01 (2005) 002 [hep-ph/0410142] [INSPIRE].
P. Fischer and D.F. Litim, Fixed points of quantum gravity in extra dimensions, Phys. Lett. B 638 (2006) 497 [hep-th/0602203] [INSPIRE].
P. Fischer and D.F. Litim, Fixed points of quantum gravity in higher dimensions, AIP Conf. Proc. 861 (2006) 336 [hep-th/0606135] [INSPIRE].
D.I. Kazakov and G.S. Vartanov, Renormalizable 1/N f expansion for field theories in extra dimensions, JHEP 06 (2007) 081 [arXiv:0707.2564] [INSPIRE].
O. Zanusso, L. Zambelli, G.P. Vacca and R. Percacci, Gravitational corrections to Yukawa systems, Phys. Lett. B 689 (2010) 90 [arXiv:0904.0938] [INSPIRE].
H. Gies, S. Rechenberger and M.M. Scherer, Towards an asymptotic-safety scenario for chiral Yukawa systems, Eur. Phys. J. C 66 (2010) 403 [arXiv:0907.0327] [INSPIRE].
J.-E. Daum, U. Harst and M. Reuter, Running gauge coupling in asymptotically safe quantum gravity, JHEP 01 (2010) 084 [arXiv:0910.4938] [INSPIRE].
G.P. Vacca and O. Zanusso, Asymptotic safety in Einstein gravity and scalar-fermion matter, Phys. Rev. Lett. 105 (2010) 231601 [arXiv:1009.1735] [INSPIRE].
X. Calmet, Asymptotically safe weak interactions, Mod. Phys. Lett. A 26 (2011) 1571 [arXiv:1012.5529] [INSPIRE].
S. Folkerts, D.F. Litim and J.M. Pawlowski, Asymptotic freedom of Yang-Mills theory with gravity, Phys. Lett. B 709 (2012) 234 [arXiv:1101.5552] [INSPIRE].
F. Bazzocchi, M. Fabbrichesi, R. Percacci, A. Tonero and L. Vecchi, Fermions and Goldstone bosons in an asymptotically safe model, Phys. Lett. B 705 (2011) 388 [arXiv:1105.1968] [INSPIRE].
H. Gies, S. Rechenberger, M.M. Scherer and L. Zambelli, An asymptotic safety scenario for gauged chiral Higgs-Yukawa models, Eur. Phys. J. C 73 (2013) 2652 [arXiv:1306.6508] [INSPIRE].
O. Antipin, M. Mojaza and F. Sannino, Conformal extensions of the standard model with Veltman conditions, Phys. Rev. D 89 (2014) 085015 [arXiv:1310.0957] [INSPIRE].
P. Doná, A. Eichhorn and R. Percacci, Matter matters in asymptotically safe quantum gravity, Phys. Rev. D 89 (2014) 084035 [arXiv:1311.2898] [INSPIRE].
A. Bonanno and M. Reuter, Cosmology of the Planck era from a renormalization group for quantum gravity, Phys. Rev. D 65 (2002) 043508 [hep-th/0106133] [INSPIRE].
K.A. Meissner and H. Nicolai, Conformal symmetry and the standard model, Phys. Lett. B 648 (2007) 312 [hep-th/0612165] [INSPIRE].
R. Foot, A. Kobakhidze, K.L. McDonald and R.R. Volkas, A solution to the hierarchy problem from an almost decoupled hidden sector within a classically scale invariant theory, Phys. Rev. D 77 (2008) 035006 [arXiv:0709.2750] [INSPIRE].
J. Hewett and T. Rizzo, Collider signals of gravitational fixed points, JHEP 12 (2007) 009 [arXiv:0707.3182] [INSPIRE].
D.F. Litim and T. Plehn, Signatures of gravitational fixed points at the LHC, Phys. Rev. Lett. 100 (2008) 131301 [arXiv:0707.3983] [INSPIRE].
M. Shaposhnikov and D. Zenhausern, Quantum scale invariance, cosmological constant and hierarchy problem, Phys. Lett. B 671 (2009) 162 [arXiv:0809.3406] [INSPIRE].
M. Shaposhnikov and D. Zenhausern, Scale invariance, unimodular gravity and dark energy, Phys. Lett. B 671 (2009) 187 [arXiv:0809.3395] [INSPIRE].
M. Shaposhnikov and C. Wetterich, Asymptotic safety of gravity and the Higgs boson mass, Phys. Lett. B 683 (2010) 196 [arXiv:0912.0208] [INSPIRE].
S. Weinberg, Asymptotically safe inflation, Phys. Rev. D 81 (2010) 083535 [arXiv:0911.3165] [INSPIRE].
G. ’t Hooft, Probing the small distance structure of canonical quantum gravity using the conformal group, arXiv:1009.0669 [INSPIRE].
E. Gerwick, D. Litim and T. Plehn, Asymptotic safety and Kaluza-Klein gravitons at the LHC, Phys. Rev. D 83 (2011) 084048 [arXiv:1101.5548] [INSPIRE].
E. Gerwick, Asymptotically safe gravitons in electroweak precision physics, Eur. Phys. J. C 71 (2011) 1676 [arXiv:1012.1118] [INSPIRE].
M. Hindmarsh, D. Litim and C. Rahmede, Asymptotically safe cosmology, JCAP 07 (2011) 019 [arXiv:1101.5401] [INSPIRE].
T. Hur and P. Ko, Scale invariant extension of the standard model with strongly interacting hidden sector, Phys. Rev. Lett. 106 (2011) 141802 [arXiv:1103.2571] [INSPIRE].
B. Dobrich and A. Eichhorn, Can we see quantum gravity? Photons in the asymptotic-safety scenario, JHEP 06 (2012) 156 [arXiv:1203.6366] [INSPIRE].
G. Marques Tavares, M. Schmaltz and W. Skiba, Higgs mass naturalness and scale invariance in the UV, Phys. Rev. D 89 (2014) 015009 [arXiv:1308.0025] [INSPIRE].
C. Tamarit, Running couplings with a vanishing scale anomaly, JHEP 12 (2013) 098 [arXiv:1309.0913] [INSPIRE].
S. Abel and A. Mariotti, Novel Higgs potentials from gauge mediation of exact scale breaking, arXiv:1312.5335 [INSPIRE].
O. Antipin, J. Krog, M. Mojaza and F. Sannino, Stable Eχtensions with(out) gravity, Nucl. Phys. B 886 (2014) 125 [arXiv:1311.1092] [INSPIRE].
M. Heikinheimo, A. Racioppi, M. Raidal, C. Spethmann and K. Tuominen, Physical naturalness and dynamical breaking of classical scale invariance, Mod. Phys. Lett. A 29 (2014) 1450077 [arXiv:1304.7006] [INSPIRE].
E. Gabrielli et al., Towards completing the standard model: vacuum stability, EWSB and dark matter, Phys. Rev. D 89 (2014) 015017 [arXiv:1309.6632] [INSPIRE].
M. Holthausen, J. Kubo, K.S. Lim and M. Lindner, Electroweak and conformal symmetry breaking by a strongly coupled hidden sector, JHEP 12 (2013) 076 [arXiv:1310.4423] [INSPIRE].
G.C. Dorsch, S.J. Huber and J.M. No, Cosmological signatures of a UV-conformal standard model, Phys. Rev. Lett. 113 (2014) 121801 [arXiv:1403.5583] [INSPIRE].
A. Eichhorn and M.M. Scherer, The Planck scale, the Higgs mass and scalar dark matter, Phys. Rev. D 90 (2014) 025023 [arXiv:1404.5962] [INSPIRE].
K. Falls, D.F. Litim, K. Nikolakopoulos and C. Rahmede, A bootstrap towards asymptotic safety, arXiv:1301.4191 [INSPIRE].
R. Gastmans, R. Kallosh and C. Truffin, Quantum gravity near two-dimensions, Nucl. Phys. B 133 (1978) 417 [INSPIRE].
S.M. Christensen and M.J. Duff, Quantum gravity in two + ϵ dimensions, Phys. Lett. B 79 (1978) 213 [INSPIRE].
M.E. Peskin, Critical point behavior of the Wilson loop, Phys. Lett. B 94 (1980) 161 [INSPIRE].
K. Gawedzki and A. Kupiainen, Exact renormalization for the Gross-Neveu model of quantum fields, Phys. Rev. Lett. 54 (1985) 2191 [INSPIRE].
K. Gawedzki and A. Kupiainen, Renormalizing the nonrenormalizable, Phys. Rev. Lett. 55 (1985) 363 [INSPIRE].
K.G. Wilson and J.B. Kogut, The renormalization group and the ϵ-expansion, Phys. Rept. 12 (1974) 75 [INSPIRE].
E. Tomboulis, 1/N expansion and renormalization in quantum gravity, Phys. Lett. B 70 (1977) 361 [INSPIRE].
E. Tomboulis, Renormalizability and asymptotic freedom in quantum gravity, Phys. Lett. B 97 (1980) 77 [INSPIRE].
L. Smolin, A fixed point for quantum gravity, Nucl. Phys. B 208 (1982) 439 [INSPIRE].
C. de Calan, P.A. Faria da Veiga, J. Magnen and R. Seneor, Constructing the three-dimensional Gross-Neveu model with a large number of flavor components, Phys. Rev. Lett. 66 (1991) 3233 [INSPIRE].
O. Antipin, M. Mojaza, C. Pica and F. Sannino, Magnetic fixed points and emergent supersymmetry, JHEP 06 (2013) 037 [arXiv:1105.1510] [INSPIRE].
O. Antipin, M. Mojaza and F. Sannino, Light dilaton at fixed points and ultra light scale super Yang-Mills, Phys. Lett. B 712 (2012) 119 [arXiv:1107.2932] [INSPIRE].
O. Antipin, S. Di Chiara, M. Mojaza, E. Mølgaard and F. Sannino, A perturbative realization of Miransky scaling, Phys. Rev. D 86 (2012) 085009 [arXiv:1205.6157] [INSPIRE].
O. Antipin, M. Gillioz, E. Mølgaard and F. Sannino, The a theorem for gauge-Yukawa theories beyond Banks-Zaks fixed point, Phys. Rev. D 87 (2013) 125017 [arXiv:1303.1525] [INSPIRE].
G. Veneziano, U(1) without instantons, Nucl. Phys. B 159 (1979) 213 [INSPIRE].
T. Banks and A. Zaks, On the phase structure of vector-like gauge theories with massless fermions, Nucl. Phys. B 196 (1982) 189 [INSPIRE].
H. Kawai, Y. Kitazawa and M. Ninomiya, Scaling exponents in quantum gravity near two-dimensions, Nucl. Phys. B 393 (1993) 280 [hep-th/9206081] [INSPIRE].
H. Kawai, Y. Kitazawa and M. Ninomiya, Ultraviolet stable fixed point and scaling relations in (2 + ϵ)-dimensional quantum gravity, Nucl. Phys. B 404 (1993) 684 [hep-th/9303123] [INSPIRE].
D.F. Litim, Fixed points of quantum gravity, Phys. Rev. Lett. 92 (2004) 201301 [hep-th/0312114] [INSPIRE].
A. Codello, R. Percacci and C. Rahmede, Investigating the ultraviolet properties of gravity with a Wilsonian renormalization group equation, Annals Phys. 324 (2009) 414 [arXiv:0805.2909] [INSPIRE].
D. Benedetti, P.F. Machado and F. Saueressig, Asymptotic safety in higher-derivative gravity, Mod. Phys. Lett. A 24 (2009) 2233 [arXiv:0901.2984] [INSPIRE].
I. Donkin and J.M. Pawlowski, The phase diagram of quantum gravity from diffeomorphism-invariant RG-flows, arXiv:1203.4207 [INSPIRE].
N. Christiansen, D.F. Litim, J.M. Pawlowski and A. Rodigast, Fixed points and infrared completion of quantum gravity, Phys. Lett. B 728 (2014) 114 [arXiv:1209.4038] [INSPIRE].
N. Christiansen, B. Knorr, J.M. Pawlowski and A. Rodigast, Global flows in quantum gravity, arXiv:1403.1232 [INSPIRE].
D. Becker and M. Reuter, En route to background independence: broken split-symmetry and how to restore it with bi-metric average actions, Annals Phys. 350 (2014) 225 [arXiv:1404.4537] [INSPIRE].
D.J. Gross and A. Neveu, Dynamical symmetry breaking in asymptotically free field theories, Phys. Rev. D 10 (1974) 3235 [INSPIRE].
Y. Kikukawa and K. Yamawaki, Ultraviolet fixed point structure of renormalizable four fermion theory in less than four-dimensions, Phys. Lett. B 234 (1990) 497 [INSPIRE].
H.-J. He, Y.-P. Kuang, Q. Wang and Y.-P. Yi, Effective potential, renormalization and nontrivial ultraviolet fixed point in D-dimensional four fermion theories (2 < D < 4) to order 1/N in 1/N expansion, Phys. Rev. D 45 (1992) 4610 [INSPIRE].
S. Hands, A. Kocic and J.B. Kogut, Four Fermi theories in fewer than four-dimensions, Annals Phys. 224 (1993) 29 [hep-lat/9208022] [INSPIRE].
J. Braun, H. Gies and D.D. Scherer, Asymptotic safety: a simple example, Phys. Rev. D 83 (2011) 085012 [arXiv:1011.1456] [INSPIRE].
H. Gies, Renormalizability of gauge theories in extra dimensions, Phys. Rev. D 68 (2003) 085015 [hep-th/0305208] [INSPIRE].
A. Pelissetto and E. Vicari, Critical phenomena and renormalization group theory, Phys. Rept. 368 (2002) 549 [cond-mat/0012164] [INSPIRE].
D.F. Litim and D. Zappala, Ising exponents from the functional renormalisation group, Phys. Rev. D 83 (2011) 085009 [arXiv:1009.1948] [INSPIRE].
L. Fei, S. Giombi and I.R. Klebanov, Critical O(N) models in 6 − ϵ dimensions, Phys. Rev. D 90 (2014) 025018 [arXiv:1404.1094] [INSPIRE].
R. Percacci and G.P. Vacca, Are there scaling solutions in the O(N)-models for large-N in d > 4?, Phys. Rev. D 90 (2014) 107702 [arXiv:1405.6622] [INSPIRE].
E. Brézin and J. Zinn-Justin, Renormalization of the nonlinear σ-model in 2 + ϵ dimensions. Application to the Heisenberg ferromagnets, Phys. Rev. Lett. 36 (1976) 691 [INSPIRE].
W.A. Bardeen, B.W. Lee and R.E. Shrock, Phase transition in the nonlinear σ-model in 2 + ϵ dimensional continuum, Phys. Rev. D 14 (1976) 985 [INSPIRE].
R. Percacci, Asymptotic safety in gravity and σ-models, PoS(CLAQG08)002 [arXiv:0910.4951] [INSPIRE].
B.H. Wellegehausen, D. Körner and A. Wipf, Asymptotic safety on the lattice: the nonlinear O(N) σ-model, Annals Phys. 349 (2014) 374 [arXiv:1402.1851] [INSPIRE].
M.E. Machacek and M.T. Vaughn, Two loop renormalization group equations in a general quantum field theory. 1. Wave function renormalization, Nucl. Phys. B 222 (1983) 83 [INSPIRE].
M.E. Machacek and M.T. Vaughn, Two loop renormalization group equations in a general quantum field theory. 2. Yukawa couplings, Nucl. Phys. B 236 (1984) 221 [INSPIRE].
M.E. Machacek and M.T. Vaughn, Two loop renormalization group equations in a general quantum field theory. 3. Scalar quartic couplings, Nucl. Phys. B 249 (1985) 70 [INSPIRE].
W.E. Caswell, Asymptotic behavior of non-Abelian gauge theories to two loop order, Phys. Rev. Lett. 33 (1974) 244 [INSPIRE].
F. Sannino, Conformal dynamics for TeV physics and cosmology, Acta Phys. Polon. B 40 (2009) 3533 [arXiv:0911.0931] [INSPIRE].
J. Kuti, The Higgs particle and the lattice, PoS(LATTICE 2013)004 [INSPIRE].
F.J. Dyson, Divergence of perturbation theory in quantum electrodynamics, Phys. Rev. 85 (1952) 631 [INSPIRE].
E. Pomoni and L. Rastelli, Large-N field theory and AdS tachyons, JHEP 04 (2009) 020 [arXiv:0805.2261] [INSPIRE].
D.F. Litim, M. Mojaza and F. Sannino, Vacuum stability of asymptotically safe gauge-Yukawa theories, in preparation.
M.-X. Luo, H.-W. Wang and Y. Xiao, Two loop renormalization group equations in general gauge field theories, Phys. Rev. D 67 (2003) 065019 [hep-ph/0211440] [INSPIRE].
I. Jack and H. Osborn, Analogs for the c theorem for four-dimensional renormalizable field theories, Nucl. Phys. B 343 (1990) 647 [INSPIRE].
I. Jack and H. Osborn, Constraints on RG flow for four dimensional quantum field theories, Nucl. Phys. B 883 (2014) 425 [arXiv:1312.0428] [INSPIRE].
O. Antipin, M. Gillioz, J. Krog, E. Mølgaard and F. Sannino, Standard model vacuum stability and Weyl consistency conditions, JHEP 08 (2013) 034 [arXiv:1306.3234] [INSPIRE].
M. Lüscher and P. Weisz, Scaling laws and triviality bounds in the lattice ϕ 4 theory. 2. One component model in the phase with spontaneous symmetry breaking, Nucl. Phys. B 295 (1988) 65 [INSPIRE].
A. Hasenfratz, K. Jansen, C.B. Lang, T. Neuhaus and H. Yoneyama, The triviality bound of the four component ϕ 4 model, Phys. Lett. B 199 (1987) 531 [INSPIRE].
O.J. Rosten, Triviality from the exact renormalization group, JHEP 07 (2009) 019 [arXiv:0808.0082] [INSPIRE].
M. Harada, Y. Kikukawa, T. Kugo and H. Nakano, Nontriviality of gauge Higgs-Yukawa system and renormalizability of gauged NJLS model, Prog. Theor. Phys. 92 (1994) 1161 [hep-ph/9407398] [INSPIRE].
J. Polchinski, Renormalization and effective Lagrangians, Nucl. Phys. B 231 (1984) 269 [INSPIRE].
C. Wetterich, Exact evolution equation for the effective potential, Phys. Lett. B 301 (1993) 90 [INSPIRE].
T.R. Morris, The exact renormalization group and approximate solutions, Int. J. Mod. Phys. A 9 (1994) 2411 [hep-ph/9308265] [INSPIRE].
D.F. Litim, Optimized renormalization group flows, Phys. Rev. D 64 (2001) 105007 [hep-th/0103195] [INSPIRE].
C. Pica and F. Sannino, β-function and anomalous dimensions, Phys. Rev. D 83 (2011) 116001 [arXiv:1011.3832] [INSPIRE].
B. Holdom, Large-N flavor β-functions: a recap, Phys. Lett. B 694 (2010) 74 [arXiv:1006.2119] [INSPIRE].
R. Shrock, Study of possible ultraviolet zero of the β-function in gauge theories with many fermions, Phys. Rev. D 89 (2014) 045019 [arXiv:1311.5268] [INSPIRE].
A. Palanques-Mestre and P. Pascual, The 1/N f expansion of the γ and β-functions in QED, Commun. Math. Phys. 95 (1984) 277 [INSPIRE].
J.A. Gracey, The QCD β-function at O(1/N f ), Phys. Lett. B 373 (1996) 178 [hep-ph/9602214] [INSPIRE].
H.W. Hamber and R.M. Williams, Quantum gravity in large dimensions, Phys. Rev. D 73 (2006) 044031 [hep-th/0512003] [INSPIRE].
N. Seiberg, Electric-magnetic duality in supersymmetric non-Abelian gauge theories, Nucl. Phys. B 435 (1995) 129 [hep-th/9411149] [INSPIRE].
F. Sannino, QCD dual, Phys. Rev. D 80 (2009) 065011 [arXiv:0907.1364] [INSPIRE].
F. Sannino, Magnetic S-parameter, Phys. Rev. Lett. 105 (2010) 232002 [arXiv:1007.0254] [INSPIRE].
Open Access
This article is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
ArXiv ePrint: 1406.2337
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Litim, D.F., Sannino, F. Asymptotic safety guaranteed. J. High Energ. Phys. 2014, 178 (2014). https://doi.org/10.1007/JHEP12(2014)178
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/JHEP12(2014)178