Abstract
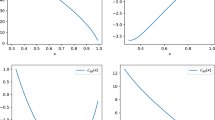
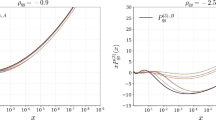
It is common lore that Parton Distribution Functions (PDFs) in the \( \overline{\mathrm{MS}} \) factorization scheme can become negative beyond leading order due to the collinear subtraction which is needed in order to define partonic cross sections. We show that this is in fact not the case and next-to-leading order (NLO) \( \overline{\mathrm{MS}} \) PDFs are actually positive in the perturbative regime. In order to prove this, we modify the subtraction prescription, and perform the collinear subtraction in such a way that partonic cross sections remain positive. This defines a factorization scheme in which PDFs are positive. We then show that positivity of the PDFs is preserved when transforming from this scheme to \( \overline{\mathrm{MS}} \), provided only the strong coupling is in the perturbative regime, such that the NLO scheme change is smaller than the LO term.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
G. Altarelli, S. Forte and G. Ridolfi, On positivity of parton distributions, Nucl. Phys. B 534 (1998) 277 [hep-ph/9806345] [INSPIRE].
S. Forte, G. Altarelli and G. Ridolfi, Are parton distributions positive?, Nucl. Phys. B Proc. Suppl. 74 (1999) 138 [hep-ph/9808462] [INSPIRE].
NNPDF collaboration, A determination of parton distributions with faithful uncertainty estimation, Nucl. Phys. B 809 (2009) 1 [Erratum ibid. 816 (2009) 293] [arXiv:0808.1231] [INSPIRE].
F. Faura, S. Iranipour, E.R. Nocera, J. Rojo and M. Ubiali, The Strangest Proton?, arXiv:2009.00014 [INSPIRE].
R.D. Ball et al., A first unbiased global NLO determination of parton distributions and their uncertainties, Nucl. Phys. B 838 (2010) 136 [arXiv:1002.4407] [INSPIRE].
NNPDF collaboration, Parton distributions for the LHC Run II, JHEP 04 (2015) 040 [arXiv:1410.8849] [INSPIRE].
R.K. Ellis, W.J. Stirling and B.R. Webber, QCD and collider physics, Camb. Monogr. Part. Phys. Nucl. Phys. Cosmol. 8 (1996) 1.
J.C. Collins and D.E. Soper, Parton Distribution and Decay Functions, Nucl. Phys. B 194 (1982) 445 [INSPIRE].
G. Curci, W. Furmanski and R. Petronzio, Evolution of Parton Densities Beyond Leading Order: The Nonsinglet Case, Nucl. Phys. B 175 (1980) 27 [INSPIRE].
J. Collins, Foundations of perturbative QCD, vol. 32, Cambridge University Press (2013).
M. Bonvini, S. Forte and G. Ridolfi, The threshold region for Higgs production in gluon fusion, Phys. Rev. Lett. 109 (2012) 102002 [arXiv:1204.5473] [INSPIRE].
S. Catani and L. Trentadue, Resummation of the QCD Perturbative Series for Hard Processes, Nucl. Phys. B 327 (1989) 323 [INSPIRE].
G.F. Sterman, Summation of Large Corrections to Short Distance Hadronic Cross-Sections, Nucl. Phys. B 281 (1987) 310 [INSPIRE].
S. Forte and G. Ridolfi, Renormalization group approach to soft gluon resummation, Nucl. Phys. B 650 (2003) 229 [hep-ph/0209154] [INSPIRE].
S. Albino and R.D. Ball, Soft resummation of quark anomalous dimensions and coefficient functions in MS-bar factorization, Phys. Lett. B 513 (2001) 93 [hep-ph/0011133] [INSPIRE].
S. Jadach, W. Płaczek, S. Sapeta, A. Siodmok and M. Skrzypek, Parton distribution functions in Monte Carlo factorisation scheme, Eur. Phys. J. C 76 (2016) 649 [arXiv:1606.00355] [INSPIRE].
F. Maltoni, Basics of QCD for the LHC: pp → H + X as a case study, CERN Yellow Rep. School Proc. 2 (2018) 41.
S. Catani, Comment on quarks and gluons at small x and the SDIS factorization scheme, Z. Phys. C 70 (1996) 263 [hep-ph/9506357] [INSPIRE].
M. Diemoz, F. Ferroni, E. Longo and G. Martinelli, Parton Densities from Deep Inelastic Scattering to Hadronic Processes at Super Collider Energies, Z. Phys. C 39 (1988) 21 [INSPIRE].
S. Jadach, private communications, (2020).
S. Forte, E. Laenen, P. Nason and J. Rojo, Heavy quarks in deep-inelastic scattering, Nucl. Phys. B 834 (2010) 116 [arXiv:1001.2312] [INSPIRE].
M.A.G. Aivazis, J.C. Collins, F.I. Olness and W.-K. Tung, Leptoproduction of heavy quarks. 2. A unified QCD formulation of charged and neutral current processes from fixed target to collider energies, Phys. Rev. D 50 (1994) 3102 [hep-ph/9312319] [INSPIRE].
M. Buza, Y. Matiounine, J. Smith and W.L. van Neerven, Charm electroproduction viewed in the variable flavor number scheme versus fixed order perturbation theory, Eur. Phys. J. C 1 (1998) 301 [hep-ph/9612398] [INSPIRE].
R.D. Ball, M. Bonvini and L. Rottoli, Charm in Deep-Inelastic Scattering, JHEP 11 (2015) 122 [arXiv:1510.02491] [INSPIRE].
NNPDF collaboration, A Determination of the Charm Content of the Proton, Eur. Phys. J. C 76 (2016) 647 [arXiv:1605.06515] [INSPIRE].
NNPDF collaboration, Parton distributions from high-precision collider data, Eur. Phys. J. C 77 (2017) 663 [arXiv:1706.00428] [INSPIRE].
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
ArXiv ePrint: 2006.07377
Rights and permissions
Open Access . This article is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Candido, A., Forte, S. & Hekhorn, F. Can \( \overline{\mathrm{MS}} \) parton distributions be negative?. J. High Energ. Phys. 2020, 129 (2020). https://doi.org/10.1007/JHEP11(2020)129
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/JHEP11(2020)129