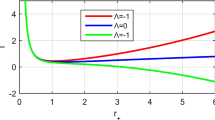
Abstract
We consider Einstein-Maxwell-dilaton gravity with the non-minimal exponential coupling between the dilaton and the Maxwell field emerging from low energy heterotic string theory. The dilaton is endowed with a potential that originates from an electromagnetic Fayet-Iliopoulos (FI) term in \( \mathcal{N} \) = 2 extended supergravity in four spacetime dimensions. For the case we are interested in, this potential introduces a single parameter α. When α → 0, the static black holes (BHs) of the model are the Gibbons-Maeda-Garfinkle-Horowitz-Strominger (GMGHS) solutions. When α → ∞, the BHs become the standard Reissner-Nordström (RN) solutions of electrovacuum General Relativity. The BH solutions for finite non-zero α interpolate between these two families. In this case, the dilaton potential regularizes the extremal limit of the GMGHS solution yielding a set of zero temperature BHs with a near horizon AdS2 × S2 geometry. We show that, in the neighborhood of these extremal solutions, there is a subset of BHs that are dynamically and thermodynamically stable, all of which have charge to mass ratio larger than unity. By dynamical stability we mean that no growing quasi-normal modes are found; thus they are stable against linear perturbations (spherical and non-spherical). Moreover, non-linear numerical evolutions lend support to their non-linear stability. By thermodynamical stability we mean the BHs are stable both in the canonical and grand-canonical ensemble. In particular, both the specific heat at constant charge and the isothermal permittivity are positive. This is not possible for RN and GMGHS BHs. We discuss the different thermodynamical phases for the BHs in this model and comment on what may allow the existence of both dynamically and thermodynamically stable BHs.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
W. Israel, Event horizons in static vacuum space-times, Phys. Rev. 164 (1967) 1776 [INSPIRE].
T. Regge and J.A. Wheeler, Stability of a Schwarzschild singularity, Phys. Rev. 108 (1957) 1063 [INSPIRE].
F.J. Zerilli, Effective potential for even parity Regge-Wheeler gravitational perturbation equations, Phys. Rev. Lett. 24 (1970) 737 [INSPIRE].
S.W. Hawking, Particle creation by black holes, Commun. Math. Phys. 43 (1975) 199 [Erratum ibid. 46 (1976) 206] [INSPIRE].
S.W. Hawking, Black holes and thermodynamics, Phys. Rev. D 13 (1976) 191 [INSPIRE].
W. Israel, Event horizons in static electrovac space-times, Commun. Math. Phys. 8 (1968) 245 [INSPIRE].
V. Moncrief, Odd-parity stability of a Reissner-Nordström black hole, Phys. Rev. D 9 (1974) 2707 [INSPIRE].
V. Moncrief, Stability of Reissner-Nordström black holes, Phys. Rev. D 10 (1974) 1057 [INSPIRE].
P.C.W. Davies, The thermodynamic theory of black holes, Proc. Roy. Soc. Lond. A 353 (1977) 499.
G.W. Gibbons, Antigravitating black hole solitons with scalar hair in n = 4 supergravity, Nucl. Phys. B 207 (1982) 337.
G.W. Gibbons and K.-I. Maeda, Black holes and membranes in higher dimensional theories with dilaton fields, Nucl. Phys. B 298 (1988) 741 [INSPIRE].
D. Garfinkle, G.T. Horowitz and A. Strominger, Charged black holes in string theory, Phys. Rev. D 43 (1991) 3140 [Erratum ibid. 45 (1992) 3888] [INSPIRE].
A. Anabalón, D. Astefanesei, A. Gallerati and M. Trigiante, Hairy black holes and duality in an extended supergravity model, JHEP 04 (2018) 058 [arXiv:1712.06971] [INSPIRE].
A. Anabalon, D. Astefanesei and R. Mann, Exact asymptotically flat charged hairy black holes with a dilaton potential, JHEP 10 (2013) 184 [arXiv:1308.1693] [INSPIRE].
D. Astefanesei, D. Choque, F. Gómez and R. Rojas, Thermodynamically stable asymptotically flat hairy black holes with a dilaton potential, JHEP 03 (2019) 205 [arXiv:1901.01269] [INSPIRE].
J.L. Blázquez-Salcedo, S. Kahlen and J. Kunz, Quasinormal modes of dilatonic Reissner-Nordstr¨om black holes, Eur. Phys. J. C 79 (2019) 1021 [arXiv:1911.01943] [INSPIRE].
A. Jansen, A. Rostworowski and M. Rutkowski, Master equations and stability of Einstein-Maxwell-scalar black holes, JHEP 12 (2019) 036 [arXiv:1909.04049] [INSPIRE].
C.A.R. Herdeiro, E. Radu, N. Sanchis-Gual and J.A. Font, Spontaneous scalarization of charged black holes, Phys. Rev. Lett. 121 (2018) 101102 [arXiv:1806.05190] [INSPIRE].
P.G.S. Fernandes, C.A.R. Herdeiro, A.M. Pombo, E. Radu and N. Sanchis-Gual, Spontaneous scalarisation of charged black holes: coupling dependence and dynamical features, Class. Quant. Grav. 36 (2019) 134002 [Erratum ibid. 37 (2020) 049501] [arXiv:1902.05079] [INSPIRE].
P.G.S. Fernandes, C.A.R. Herdeiro, A.M. Pombo, E. Radu and N. Sanchis-Gual, Charged black holes with axionic-type couplings: classes of solutions and dynamical scalarization, Phys. Rev. D 100 (2019) 084045 [arXiv:1908.00037] [INSPIRE].
C.W. Misner and D.H. Sharp, Relativistic equations for adiabatic, spherically symmetric gravitational collapse, Phys. Rev. 136 (1964) B571 [INSPIRE].
D. Astefanesei, R. Ballesteros, D. Choque and R. Rojas, Scalar charges and the first law of black hole thermodynamics, Phys. Lett. B 782 (2018) 47 [arXiv:1803.11317] [INSPIRE].
C.A.R. Herdeiro and E. Radu, Asymptotically flat black holes with scalar hair: a review, Int. J. Mod. Phys. D 24 (2015) 1542014 [arXiv:1504.08209] [INSPIRE].
K. Goldstein, N. Iizuka, R.P. Jena and S.P. Trivedi, Non-supersymmetric attractors, Phys. Rev. D 72 (2005) 124021 [hep-th/0507096] [INSPIRE].
A. Sen, Black hole entropy function and the attractor mechanism in higher derivative gravity, JHEP 09 (2005) 038 [hep-th/0506177] [INSPIRE].
D. Astefanesei, K. Goldstein, R.P. Jena, A. Sen and S.P. Trivedi, Rotating attractors, JHEP 10 (2006) 058 [hep-th/0606244] [INSPIRE].
A. Sen, Black hole entropy function, attractors and precision counting of microstates, Gen. Rel. Grav. 40 (2008) 2249 [arXiv:0708.1270] [INSPIRE].
A. Anabalón and D. Astefanesei, On attractor mechanism of AdS4 black holes, Phys. Lett. B 727 (2013) 568 [arXiv:1309.5863] [INSPIRE].
I. Robinson, A solution of the Maxwell-Einstein equations, Bull. Acad. Pol. Sci. Ser. Sci. Math. Astron. Phys. 7 (1959) 351.
B. Bertotti, Uniform electromagnetic field in the theory of general relativity, Phys. Rev. 116 (1959) 1331 [INSPIRE].
J.L. Blázquez-Salcedo, D.D. Doneva, J. Kunz and S.S. Yazadjiev, Radial perturbations of the scalarized Einstein-Gauss-Bonnet black holes, Phys. Rev. D 98 (2018) 084011 [arXiv:1805.05755] [INSPIRE].
K.D. Kokkotas and B.G. Schmidt, Quasinormal modes of stars and black holes, Living Rev. Rel. 2 (1999) 2 [gr-qc/9909058] [INSPIRE].
H.-P. Nollert, Quasinormal modes: the characteristic ‘sound’ of black holes and neutron stars, Class. Quant. Grav. 16 (1999) R159 [INSPIRE].
E. Berti, V. Cardoso and A.O. Starinets, Quasinormal modes of black holes and black branes, Class. Quant. Grav. 26 (2009) 163001 [arXiv:0905.2975] [INSPIRE].
R.A. Konoplya and A. Zhidenko, Quasinormal modes of black holes: from astrophysics to string theory, Rev. Mod. Phys. 83 (2011) 793 [arXiv:1102.4014] [INSPIRE].
V. Ferrari, M. Pauri and F. Piazza, Quasinormal modes of charged, dilaton black holes, Phys. Rev. D 63 (2001) 064009 [gr-qc/0005125] [INSPIRE].
J.L. Blázquez-Salcedo et al., Quasinormal modes of compact objects in alternative theories of gravity, Eur. Phys. J. Plus 134 (2019) 46 [arXiv:1810.09432] [INSPIRE].
E.W. Leaver, Quasinormal modes of Reissner-Nordström black holes, Phys. Rev. D 41 (1990) 2986 [INSPIRE].
J.L. Blázquez-Salcedo et al., Perturbed black holes in Einstein-dilaton-Gauss-Bonnet gravity: stability, ringdown and gravitational-wave emission, Phys. Rev. D 94 (2016) 104024 [arXiv:1609.01286] [INSPIRE].
J.L. Blázquez-Salcedo, F.S. Khoo and J. Kunz, Quasinormal modes of Einstein-Gauss-Bonnet-dilaton black holes, Phys. Rev. D 96 (2017) 064008 [arXiv:1706.03262] [INSPIRE].
N. Sanchis-Gual, J.C. Degollado, P.J. Montero, J.A. Font and C. Herdeiro, Explosion and final state of an unstable Reissner-Nordström black hole, Phys. Rev. Lett. 116 (2016) 141101 [arXiv:1512.05358] [INSPIRE].
N. Sanchis-Gual, J.C. Degollado, C. Herdeiro, J.A. Font and P.J. Montero, Dynamical formation of a Reissner-Nordström black hole with scalar hair in a cavity, Phys. Rev. D 94 (2016) 044061 [arXiv:1607.06304] [INSPIRE].
E.W. Hirschmann, L. Lehner, S.L. Liebling and C. Palenzuela, Black hole dynamics in Einstein-Maxwell-dilaton theory, Phys. Rev. D 97 (2018) 064032 [arXiv:1706.09875] [INSPIRE].
I. Cordero-Carrion and P. Cerda-Duran, Partially implicit Runge-Kutta methods for wave-like equations in spherical-type coordinates, arXiv:1211.5930 [INSPIRE].
I. Cordero-Carrión and P. Cerdá-Durán, Partially implicit Runge-Kutta methods for wave-like equations, in Advances in differential equations and applications, Springer, Cham, Switzerland (2014), pg. 267.
Einstein toolkit: open software for relativistic astrophysics webpage, http://einsteintoolkit.org/.
F. Löffler et al., The Einstein toolkit: a community computational infrastructure for relativistic astrophysics, Class. Quant. Grav. 29 (2012) 115001 [arXiv:1111.3344] [INSPIRE].
G.W. Gibbons, R. Kallosh and B. Kol, Moduli, scalar charges and the first law of black hole thermodynamics, Phys. Rev. Lett. 77 (1996) 4992 [hep-th/9607108] [INSPIRE].
H. Lü, Y. Pang and C.N. Pope, AdS dyonic black hole and its thermodynamics, JHEP 11 (2013) 033 [arXiv:1307.6243] [INSPIRE].
H. Lü, C.N. Pope and Q. Wen, Thermodynamics of AdS black holes in Einstein-scalar gravity, JHEP 03 (2015) 165 [arXiv:1408.1514] [INSPIRE].
A. Anabalon, D. Astefanesei and C. Martinez, Mass of asymptotically anti-de Sitter hairy spacetimes, Phys. Rev. D 91 (2015) 041501 [arXiv:1407.3296] [INSPIRE].
A. Anabalon, D. Astefanesei, D. Choque and C. Martinez, Trace anomaly and counterterms in designer gravity, JHEP 03 (2016) 117 [arXiv:1511.08759] [INSPIRE].
J. Brown and J.W. York, Quasilocal energy and conserved charges derived from the gravitational action, Phys. Rev. D 47 (1993) 1407 [gr-qc/9209012] [INSPIRE].
T. Hertog and G.T. Horowitz, Designer gravity and field theory effective potentials, Phys. Rev. Lett. 94 (2005) 221301 [hep-th/0412169] [INSPIRE].
Open Access
This article is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
ArXiv ePrint: 1912.02192
Rights and permissions
Open Access . This article is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Astefanesei, D., Blázquez-Salcedo, J.L., Herdeiro, C. et al. Dynamically and thermodynamically stable black holes in Einstein-Maxwell-dilaton gravity. J. High Energ. Phys. 2020, 63 (2020). https://doi.org/10.1007/JHEP07(2020)063
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/JHEP07(2020)063