Skip to main content
Download PDF

Holographic duality between local Hamiltonians from random tensor networks

Journal of High Energy Physics volume 2022, Article number: 52 (2022) Cite this article

A preprint version of the article is available at arXiv.

Abstract

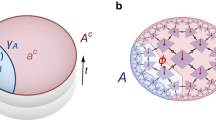
The AdS/CFT correspondence realises the holographic principle where information in the bulk of a space is encoded at its border. We are yet a long way from a full mathematical construction of AdS/CFT, but toy models in the form of holographic quantum error correcting codes (HQECC) have replicated some interesting features of the correspondence. In this work we construct new HQECCs built from random stabilizer tensors that describe a duality between models encompassing local Hamiltonians whilst exactly obeying the Ryu-Takayanagi entropy formula for all boundary regions. We also obtain complementary recovery of local bulk operators for any boundary bipartition. Existing HQECCs have been shown to exhibit these properties individually, whereas our mathematically rigorous toy models capture these features of AdS/CFT simultaneously, advancing further towards a complete construction of holographic duality.

References

  1. G. ’t Hooft, Dimensional reduction in quantum gravity, Conf. Proc. C 930308 (1993) 284 [gr-qc/9310026] [INSPIRE].

  2. L. Susskind, The world as a hologram, J. Math. Phys. 36 (1995) 6377 [hep-th/9409089] [INSPIRE].

    ADS  MathSciNet  Article  Google Scholar 

  3. A. Almheiri, X. Dong and D. Harlow, Bulk locality and quantum error correction in AdS/CFT, JHEP 04 (2015) 163 [arXiv:1411.7041] [INSPIRE].

    ADS  MathSciNet  Article  Google Scholar 

  4. F. Pastawski, B. Yoshida, D. Harlow and J. Preskill, Holographic quantum error-correcting codes: toy models for the bulk/boundary correspondence, JHEP 06 (2015) 149 [arXiv:1503.06237] [INSPIRE].

    ADS  MathSciNet  Article  Google Scholar 

  5. T. Kohler and T. Cubitt, Toy models of holographic duality between local Hamiltonians, JHEP 08 (2019) 017 [arXiv:1810.08992] [INSPIRE].

    ADS  MathSciNet  Article  Google Scholar 

  6. P. Hayden, S. Nezami, X.-L. Qi, N. Thomas, M. Walter and Z. Yang, Holographic duality from random tensor networks, JHEP 11 (2016) 009 [arXiv:1601.01694] [INSPIRE].

    ADS  MathSciNet  Article  Google Scholar 

  7. A. Bhattacharyya, Z.-S. Gao, L.-Y. Hung and S.-N. Liu, Exploring the tensor networks/AdS correspondence, JHEP 08 (2016) 086 [arXiv:1606.00621] [INSPIRE].

    ADS  MathSciNet  Article  Google Scholar 

  8. T.J. Osborne and D.E. Stiegemann, Dynamics for holographic codes, JHEP 04 (2020) 154 [arXiv:1706.08823] [INSPIRE].

    ADS  MathSciNet  Article  Google Scholar 

  9. B. Swingle, Constructing holographic spacetimes using entanglement renormalization, arXiv:1209.3304 [INSPIRE].

  10. Z. Yang, P. Hayden and X.-L. Qi, Bidirectional holographic codes and sub-AdS locality, JHEP 01 (2016) 175 [arXiv:1510.03784] [INSPIRE].

    ADS  MathSciNet  Article  Google Scholar 

  11. B. Swingle, Entanglement renormalization and holography, Phys. Rev. D 86 (2012) 065007 [arXiv:0905.1317] [INSPIRE].

  12. T. Kohler, S. Piddock, J. Bausch and T. Cubitt, Translationally invariant universal quantum hamiltonians in 1D, Annales Henri Poincaré 23 (2022) 223 [arXiv:2003.13753] [INSPIRE].

    MathSciNet  Article  Google Scholar 

  13. T. Faulkner, A. Lewkowycz and J. Maldacena, Quantum corrections to holographic entanglement entropy, JHEP 11 (2013) 074 [arXiv:1307.2892] [INSPIRE].

    ADS  Article  Google Scholar 

  14. A.C. Wall, Maximin surfaces, and the strong subadditivity of the covariant holographic entanglement entropy, Class. Quant. Grav. 31 (2014) 225007 [arXiv:1211.3494] [INSPIRE].

  15. T.S. Cubitt, A. Montanaro and S. Piddock, Universal quantum hamiltonians, Proc. Nat. Acad. Sci. 115 (2018) 9497.

    ADS  MathSciNet  Article  Google Scholar 

  16. R. Oliveira and B. Terhal, The complexity of quantum spin systems on a two-dimensional square lattice, Quant. Informat. Comput. 8 (2008) 900 [quant-ph/0504050].

    MathSciNet  MATH  Google Scholar 

  17. W. Helwig and W. Cui, Absolutely maximally entangled states: existence and applications, arXiv:1306.2536.

  18. S. Rubinstein, On the existence and uniqueness of invariant measures on locally compact groups, (2004).

  19. C. Dankert, R. Cleve, J. Emerson and E. Livine, Exact and approximate unitary 2-designs and their application to fidelity estimation, Phys. Rev. A 80 (2009) 012304.

  20. W. Dür, M. Hein, J.I. Cirac and H.-J. Briegel, Standard forms of noisy quantum operations via depolarization, Phys. Rev. A 72 (2005) 052326.

  21. H. Chau, Unconditionally secure key distribution in higher dimensions by depolarization, IEEE Trans. Inform. Theory 51 (2005) 1451 [quant-ph/0405016].

    MathSciNet  Article  Google Scholar 

  22. J. Tits, Groupes et géométries de Coxeter (in French), unpublished manuscript, (1961).

  23. M.W. Davis, The geometry and topology of Coxeter groups, Princeton University Press, Princeton, NJ, U.S.A. (2012).

  24. E.B. Vinberg, Discrete groups generated by reflections in Lobačevskĭ space, Math. USSR-Sbornik 1 (1967) 429.

    Article  Google Scholar 

  25. P. Hayden, D.W. Leung and A. Winter, Aspects of generic entanglement, Commun. Math. Phys. 265 (2006) 95.

    ADS  MathSciNet  Article  Google Scholar 

  26. M. Ledoux, The concentration of measure phenomenon, volume 89 of Mathematical surveys and monographs, American Mathematical Society, Providence, RI, U.S.A. (2001).

  27. R.A. Low, Large deviation bounds for k-designs, Proc. Roy. Soc. A 465 (2009) 3289.

    ADS  MathSciNet  Article  Google Scholar 

  28. A.W. Harrow, The church of the symmetric subspace, arXiv:1308.6595.

  29. D. Fattal, T. Cubitt, Y. Yamamoto, S. Bravyi and I. Chuang, Entanglement in the stabilizer formalism, quant-ph/0406168.

  30. M. Fréchet, Généralisation du théorème des probabilités totales (in French), Fund. Math. 25 (1935) 379.

  31. M. Fréchet, Sur les tableaux de corrélation dont les marges sont données (in French), Ann. Univ. Lyon A 9 (1951) 53.

  32. S. Nezami and M. Walter, Multipartite entanglement in stabilizer tensor networks, Phys. Rev. Lett. 125 (2020) 241602 [arXiv:1608.02595] [INSPIRE].

  33. S.W. Hawking and D.N. Page, Thermodynamics of black holes in anti-de Sitter space, Commun. Math. Phys. 87 (1983) 577 [INSPIRE].

  34. I. Heemskerk, J. Penedones, J. Polchinski and J. Sully, Holography from conformal field theory, JHEP 10 (2009) 079 [arXiv:0907.0151] [INSPIRE].

    ADS  MathSciNet  Article  Google Scholar 

  35. S. El-Showk and K. Papadodimas, Emergent spacetime and holographic CFTs, JHEP 10 (2012) 106 [arXiv:1101.4163] [INSPIRE].

    ADS  Article  Google Scholar 

  36. S. Piddock and A. Montanaro, Universal qudit Hamiltonians, arXiv:1802.07130.

  37. X. Dong, The gravity dual of Rényi entropy, Nature Commun. 7 (2016) 12472 [arXiv:1601.06788] [INSPIRE].

    ADS  Article  Google Scholar 

  38. X. Dong, D. Harlow and D. Marolf, Flat entanglement spectra in fixed-area states of quantum gravity, JHEP 10 (2019) 240 [arXiv:1811.05382] [INSPIRE].

    ADS  MathSciNet  Article  Google Scholar 

  39. M. Han and S. Huang, Discrete gravity on random tensor network and holographic Rényi entropy, JHEP 11 (2017) 148 [arXiv:1705.01964] [INSPIRE].

    ADS  Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science, University College London, Gower St., London, WC1E 6EA, UK

    Harriet Apel, Tamara Kohler & Toby Cubitt

Authors
  1. Harriet Apel
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tamara Kohler
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Toby Cubitt
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Harriet Apel.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

ArXiv ePrint: 2105.12067

Rights and permissions

Open Access . This article is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Apel, H., Kohler, T. & Cubitt, T. Holographic duality between local Hamiltonians from random tensor networks. J. High Energ. Phys. 2022, 52 (2022). https://doi.org/10.1007/JHEP03(2022)052

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/JHEP03(2022)052

Keywords

  • AdS-CFT Correspondence
  • Gauge-Gravity Correspondence
  • Models of Quantum Gravity
  • Random Systems