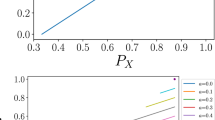Abstract
Purification is a powerful technique in quantum physics whereby a mixed quantum state is extended to a pure state on a larger system. This process is not unique, and in systems composed of many degrees of freedom, one natural purification is the one with minimal entanglement. Here we study the entropy of the minimally entangled purification, called the entanglement of purification, in three model systems: an Ising spin chain, conformal field theories holographically dual to Einstein gravity, and random stabilizer tensor networks. We conjecture values for the entanglement of purification in all these models, and we support our conjectures with a variety of numerical and analytical results. We find that such minimally entangled purifications have a number of applications, from enhancing entanglement-based tensor network methods for describing mixed states to elucidating novel aspects of the emergence of geometry from entanglement in the AdS/CFT correspondence.
Article PDF
Similar content being viewed by others
References
A.E. Feiguin and S.R. White, Finite-temperature density matrix renormalization using an enlarged Hilbert space, Phys. Rev. B 72 (2005) 220401 [cond-mat/0510124].
J.M. Maldacena, The large-N limit of superconformal field theories and supergravity, Int. J. Theor. Phys. 38 (1999) 1113 [hep-th/9711200] [INSPIRE].
E. Witten, Anti-de Sitter space and holography, Adv. Theor. Math. Phys. 2 (1998) 253 [hep-th/9802150] [INSPIRE].
S.S. Gubser, I.R. Klebanov and A.M. Polyakov, Gauge theory correlators from noncritical string theory, Phys. Lett. B 428 (1998) 105 [hep-th/9802109] [INSPIRE].
W. Israel, Thermo field dynamics of black holes, Phys. Lett. A 57 (1976) 107 [INSPIRE].
J.M. Maldacena, Eternal black holes in anti-de Sitter, JHEP 04 (2003) 021 [hep-th/0106112] [INSPIRE].
B. Swingle, Entanglement renormalization and holography, Phys. Rev. D 86 (2012) 065007 [arXiv:0905.1317] [INSPIRE].
B.M. Terhal, M. Horodecki, D.W. Leung and D.P. DiVincenzo, The entanglement of purification, J. Math. Phys. 43 (2002) 4286 [quant-ph/0202044].
P. Hayden, S. Nezami, X.-L. Qi, N. Thomas, M. Walter and Z. Yang, Holographic duality from random tensor networks, JHEP 11 (2016) 009 [arXiv:1601.01694] [INSPIRE].
S. Nezami and M. Walter, Multipartite entanglement in stabilizer tensor networks, arXiv:1608.02595 [INSPIRE].
M. Fannes, B. Nachtergaele and R.F. Werner, Finitely correlated states on quantum spin chains, Commun. Math. Phys. 144 (1992) 443 [INSPIRE].
S. Ryu and T. Takayanagi, Holographic derivation of entanglement entropy from AdS/CFT, Phys. Rev. Lett. 96 (2006) 181602 [hep-th/0603001] [INSPIRE].
S. Bagchi and A.K. Pati, Monogamy, polygamy, and other properties of entanglement of purification, Phys. Rev. A 91 (2015) 042323 [arXiv:1502.01272].
M. Headrick, V.E. Hubeny, A. Lawrence and M. Rangamani, Causality & holographic entanglement entropy, JHEP 12 (2014) 162 [arXiv:1408.6300] [INSPIRE].
B. Czech, J.L. Karczmarek, F. Nogueira and M. Van Raamsdonk, The gravity dual of a density matrix, Class. Quant. Grav. 29 (2012) 155009 [arXiv:1204.1330] [INSPIRE].
D.L. Jafferis, A. Lewkowycz, J. Maldacena and S.J. Suh, Relative entropy equals bulk relative entropy, JHEP 06 (2016) 004 [arXiv:1512.06431] [INSPIRE].
T. Takayanagi and K. Umemoto, Holographic entanglement of purification, arXiv:1708.09393 [INSPIRE].
F. Pastawski, B. Yoshida, D. Harlow and J. Preskill, Holographic quantum error-correcting codes: toy models for the bulk/boundary correspondence, JHEP 06 (2015) 149 [arXiv:1503.06237] [INSPIRE].
P. Calabrese, J. Cardy and E. Tonni, Entanglement negativity in quantum field theory, Phys. Rev. Lett. 109 (2012) 130502 [arXiv:1206.3092] [INSPIRE].
P. Chaturvedi, V. Malvimat and G. Sengupta, Entanglement negativity, holography and black holes, arXiv:1602.01147 [INSPIRE].
M. Bañados, C. Teitelboim and J. Zanelli, The black hole in three-dimensional space-time, Phys. Rev. Lett. 69 (1992) 1849 [hep-th/9204099] [INSPIRE].
V.E. Hubeny, H. Maxfield, M. Rangamani and E. Tonni, Holographic entanglement plateaux, JHEP 08 (2013) 092 [arXiv:1306.4004] [INSPIRE].
J. Hauschild, E. Altman, M. Zaletel and F. Pollmann, Finding purifications with minimal entanglement, under final preparation.
S. Östlund and S. Rommer, Thermodynamic limit of density matrix renormalization for the spin-1 Heisenberg chain, Phys. Rev. Lett. 75 (1995) 3537 [cond-mat/9503107] [INSPIRE].
F. Verstraete, J.J. García-Ripoll and J.I. Cirac, Matrix product density operators: simulation of finite-temperature and dissipative systems, Phys. Rev. Lett. 93 (2004) 207204.
U. Schollwöck, The density-matrix renormalization group in the age of matrix product states, Ann. Phys. 326 (2011) 96 [arXiv:1008.3477].
C. Karrasch, J.H. Bardarson and J.E. Moore, Reducing the numerical effort of finite-temperature density matrix renormalization group calculations, New J. Phys. 15 (2013) 083031.
G. Vidal, Classical simulation of infinite-size quantum lattice systems in one spatial dimension, Phys. Rev. Lett. 98 (2007) 070201 [cond-mat/0605597] [INSPIRE].
G. Evenbly and G. Vidal, Algorithms for entanglement renormalization, Phys. Rev. B 79 (2009) 144108 [arXiv:0707.1454] [INSPIRE].
I. Peschel and V. Eisler, Reduced density matrices and entanglement entropy in free lattice models, J. Phys. A 42 (2009) 504003 [arXiv:0906.1663].
T. Takayanagi, Holographic dual of BCFT, Phys. Rev. Lett. 107 (2011) 101602 [arXiv:1105.5165] [INSPIRE].
S.Y. Looi and R.B. Griffiths, Tripartite entanglement in qudit stabilizer states and application in quantum error correction, Phys. Rev. A 84 (2011) 052306.
S. Bravyi, D. Fattal and D. Gottesman, GHZ extraction yield for multipartite stabilizer states, J. Math. Phys. 47 (2006) 062106.
V.E. Hubeny, M. Rangamani and T. Takayanagi, A covariant holographic entanglement entropy proposal, JHEP 07 (2007) 062 [arXiv:0705.0016] [INSPIRE].
T. Hartman and J. Maldacena, Time evolution of entanglement entropy from black hole interiors, JHEP 05 (2013) 014 [arXiv:1303.1080] [INSPIRE].
I.A. Morrison and M.M. Roberts, Mutual information between thermo-field doubles and disconnected holographic boundaries, JHEP 07 (2013) 081 [arXiv:1211.2887] [INSPIRE].
P. Hayden, M. Headrick and A. Maloney, Holographic mutual information is monogamous, Phys. Rev. D 87 (2013) 046003 [arXiv:1107.2940] [INSPIRE].
A.C. Wall, Maximin surfaces and the strong subadditivity of the covariant holographic entanglement entropy, Class. Quant. Grav. 31 (2014) 225007 [arXiv:1211.3494] [INSPIRE].
B. Czech, P. Hayden, N. Lashkari and B. Swingle, The information theoretic interpretation of the length of a curve, JHEP 06 (2015) 157 [arXiv:1410.1540] [INSPIRE].
M. Freedman and M. Headrick, Bit threads and holographic entanglement, Commun. Math. Phys. 352 (2017) 407 [arXiv:1604.00354] [INSPIRE].
E. Beltrami, Saggio di interpretazione della geometria non-euclidea (in Italian), Giornale di Mathematiche VI (1868) 285.
E. Beltrami, Teoria fondamentale degli spazii di curvatura costante (in Italian), Annali. Mat. Ser. II 2 (1868) 232.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
ArXiv ePrint: 1709.07424
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Nguyen, P., Devakul, T., Halbasch, M.G. et al. Entanglement of purification: from spin chains to holography. J. High Energ. Phys. 2018, 98 (2018). https://doi.org/10.1007/JHEP01(2018)098
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/JHEP01(2018)098