Skip to main content
SpringerLink
Log in

An unstructured-grid based volume-of-fluid method for extreme wave and freely-floating structure interactions

  • Session A7
  • Published:
Journal of Hydrodynamics Aims and scope Submit manuscript

Abstract

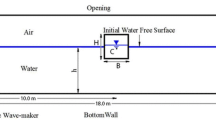
A Volume of Fluid (VOF) technique has been further developed and coupled with an incompressible Euler/Navier Stokes solver operating on adaptive, unstructured grids to simulate the interactions of extreme waves and a LNG carrier with full or partially filled tanks. The present implementation follows the classic VOF implementation for the liquid-gas system, considering only the liquid phase. Extrapolation algorithms are used to obtain velocities and pressures in the gas region near the free surface. An arbitrary Lagrangian-Eulerian (ALE) frame of reference is used. The mesh is moved in such a way as to minimize the distortion of the mesh due to body movement. The incompressible Euler/Navier-Stokes equations are solved using projection schemes and a finite element method on unstructured grids, and the free surface is captured by the VOF method. The computer code developed based on the method described above is used in this study to simulate a numerical seakeeping tank, where the waves are generated by the sinusoidal excitation of a piston paddle, and a freely-floating LNG carrier with full or partially filled tanks moves in response to the waves. Both head sea and oblique sea are considered in the simulation. Highly nonlinear wave-body interactions, such as green water on deck and sloshing, have been modeled successfully.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Nichols, B.D. and Hirt, C.W. Methods for Calculating Multi-Dimensional, Transient Free Surface Flows Past Bodies, Proc. First Intern. Conf. Num. Ship Hydrodynamics, Research Gaithersburg, ML, Oct. 20–23 (1975).

  2. Hirt, C.W. and Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries, Journal of Computational Physics 39, 201 (1981).

    Article  Google Scholar 

  3. Scardovelli, R.; Zaleski, S. Direct numerical simulation of free-surface and interfacial Flow, Annual Review of Fluid Mechanics 31: 567–603 (1999).

    Article  MathSciNet  Google Scholar 

  4. Chen, G., Kharif, C. Two-Dimensional Navier-Stokes Simulation of Breaking Waves, Physics of Fluids, 11(1), 121–133, (1999).

    Article  Google Scholar 

  5. Biausser, B., Fraunie, P., Grilli, S. and Marcer R. Numerical analysis of the internal kinematics and dynamics of three dimensional breaking waves on slopes, International Journal of Offshore and Polar Engineering, Vol. 14, No. 4 (2004).

  6. Fekken, G., Veldman, A.E.P. and Buchner, B. Simulation of Green Water Loading Using the Navier-Stokes Equations, Proc. of the 7th Int. Conf. on Numerical Ship Hydrodynamics, Nantes, France (1999).

    Google Scholar 

  7. Huijsmans, R.H.M. and van Grosen, E. Coupling Freak Wave Effects with Green Water Simulations, Proceeding of the 14th ISOPE, Toulon, France, May 23–28 (2004).

  8. Rhee, S.H. Unstructured Grid Based Reynolds-Averaged Navier-Stokes Method for Liquid Tank Sloshing, Journal of Fluids Engineering, Volume 127, Issue 3, pp. 572–582 (2005).

    Article  Google Scholar 

  9. Yang, C. and Löhner, R. Computation of 3D Flows with Violent Free Surface Motion, Proceeding of the 15th ISOPE, Seoul, Korea, June 19–24 (2005).

  10. Löhner, R. A Fast Finite Element Solver for Incompressible Flows, AIAA-90-0398 (1990).

  11. Löhner, R. A Fast Finite Element Solver for Incompressible Flows, AIAA-90-0398 (1993).

  12. Yang, C. and Löhner, R. Fully Nonlinear Ship Wave Calculation Using Unstructured Grids and Parallel Computing, Proc. 3rd Osaka Col. on Advanced CFD Appl. to Ship Flow and Hull Form Design, Osaka, Japan (1998).

  13. Löhner, R., Yang, C., Onate, E. and Idelssohn, S. An Unstructured Grid-Based, Parallel Free Surface Solver, Appl. Num. Math. 31, 271–293 (1999).

    Article  MathSciNet  Google Scholar 

  14. Löhner, R. Applied CFD Techniques; J. Wiley & Sons (2001).

  15. Löhner, R. Multistage Explicit Advective Prediction for Projection-Type Incompressible Flow Solvers, J. Comp. Phys. 195, 143–152 (2004).

    Article  Google Scholar 

  16. Löhner, R., Yang, C., Cebral, J., Camelli, F., Soto, O. and Waltz, J. Improving the Speed and Accuracy of Projection-Type Incompressible Flow Solvers, Computer Methods in Applied Mechanics and Engineering, Vol. 195, Issues 23–24, April 2006, pp. 3087–3109.

    Article  MathSciNet  Google Scholar 

  17. Martin, J.C. and Moyce, W.J. An Experimental Study of the Collapse of a Liquid Column on a Rigid Horizontal Plane, Phil. Trans. Royal Soc. London A244, 312–324 (1952).

    Article  Google Scholar 

  18. Hansbo, P. The Characteristic Streamline Diffusion Method for the Time-Dependent Incompressible Navier-Stokes Equations, Comp. Meth. Appl. Mech. Eng. 99, 171–186 (1992).

    Article  MathSciNet  Google Scholar 

  19. Köolke, A. Modellierung und Diskretisierung bewegter Diskontinuit’aten in Randgekoppelten Mehrfeldaufgaben, Ph.D. Thesis, TU Braunschweig (2005).

  20. Landrini, M., Colagorossi, A. and Faltisen, O.M. Sloshing in 2-D Flows by the SPH Method, Proc. of the 8th Int. Conf. on Num. Ship Hydro., Busan, Korea (2003).

Download references

Author information

Authors and Affiliations

  1. School of Computational Sciences, George Mason University, Fairfax, Virginia, USA

    Chi Yang, Rainald Löhner & Haidong Lu

  2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai, China

    Chi Yang

Authors
  1. Chi Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rainald Löhner
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Haidong Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chi Yang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yang, C., Löhner, R. & Lu, H. An unstructured-grid based volume-of-fluid method for extreme wave and freely-floating structure interactions. J Hydrodyn 18 (Suppl 1), 405–412 (2006). https://doi.org/10.1007/BF03400480

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03400480

Key words

Search

Navigation