Skip to main content
SpringerLink
Log in

An ordering policy for deteriorating items with two component demand and price breaks allowing shortages

  • Published:
OPSEARCH Aims and scope Submit manuscript

An Erratum to this article was published on 01 September 2007

Abstract

This paper deals with an EOQ model of an inventory problem with a two-component demand rate:

  1. (i)

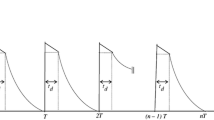
    For a certain period the demand rate is quadratic depending on stock.

  2. (ii)

    For the rest of the cycle the demand rate is constant.

Price breaks are also taken into account. Effects of deterioration are considered.

This paper considers an EOQ model with a two-component demand rate, deterioration of items and price breaks. Shortages are allowed. The effectiveness of this model is illustrated with a numerical example and sensitivity analysis has been performed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Teng, J.T. and Chang, C.T. (2005), “Economic production quantity models for deteriorating items with price and stock dependent demand”, Computers and Operational Research, Vol.32, pp. 297–308.

    Article  Google Scholar 

  2. Rao. K.S. and Sarma. K.V.S. (2004), “An order-level inventory model under L2 system with power pattern demand”. International Journal of Management and Systems, Vol.20, pp. 31–40.

    Google Scholar 

  3. Rau, H; Wu, M.Y. and Wee, H.M. (2004), “Deteriorating item inventory model with shortage due to supplier in an integrated supply chain”, International Journal of System Science, Vol.35(5), pp. 293–303.

    Article  Google Scholar 

  4. Subbaiah, K.V; Rao, K.S and Satyanarayana, B. (2004), “Inventory models for perishable items having demand rate dependent on stock level”, Opsearch, Vol.41(4), pp. 223–236.

    Article  Google Scholar 

  5. Abad, P.I, (2003), “Optimal price and lot size when the supplier offers a temporary price reduction over an interval”, Computers & Operations Research, 30, 63–74.

    Article  Google Scholar 

  6. Arcelus, F.J and Srinivasan, G (2003), “Forward buying policies for deteriorating items under price sensitive demand and temporary price discount”, IJOQM, Vol.9, No.2, 87–101.

    Google Scholar 

  7. Chung, K.J and Hwang, Y.F (2003), “The optimal cycle time for EOQ inventory model under permissible delay in payments”, International journal of Production Economics, 84, 307–318.

    Article  Google Scholar 

  8. Skouri, K, Papachritos, S (2003), “Optimal stoping and restarting production times for an EOQ model with deteriorating items and time-dependent partial backlogging”, International Journal of ProductionEconomics, 81–82, 525–531.

    Article  Google Scholar 

  9. Dye, C.Y (2002), “A deteriorating inventory model with stock dependent demand and partial back-logging under conditions of permissible delay in payments”, Opsearch, Vol.39, No.3 & 4.

  10. Matsuyama, K. (2001), “The EOQ model modified by introducing discount of purchase price or increase of set-up cost”, “International Journal of Production Economics”, 73, 83–99.

    Article  Google Scholar 

  11. Reddy, G.S.N and Sarma, K.V.S (2001), “A periodic review inventory problem with variable stock dependent demand “’Opsearch, Vol.38, No.3, 332–341.

    Article  Google Scholar 

  12. Schniederjans, M.J, Cao, Q, (2000) “A note on JIT purchasing vs. EOQ with a price discount: an expansion of inventory costs”, International Journal of Production Economics, 65, 289–294.

    Article  Google Scholar 

  13. Abad, P.I, (1998), “Determining optimal selling price and lot size when the supplier offers all-unit quantity discounts”, Decisions Sciences, 19, 622–634.

    Article  Google Scholar 

  14. Fazal, F, Fischer, K.P and E.W. Gilbert. (1998) “J.I.T. purchasing vs. EOQ with a price discount. An analytical comparison of inventory costs”, International journal of Production Economics, 54, 101–109.

    Article  Google Scholar 

  15. Jamal, A, Sarkar, B and Wang, S. (l997), “An ordering policy for deteriorating items with allowable shortages and permisiible delay in payments”, Journal of Operational Research Society, 826–833.

  16. Paul, K, Dutta, T.K, Chaudhuri K.S and Pal, A.K, (1996), “An inventory model with two component demand rate and shortages”, Journal of Operational Research Society, 47 1029–1036.

    Article  Google Scholar 

  17. Wee, H (1995), “A deterministic lot size inventory model for deteriorating items with shortage and a declining market” Computers & Operations Research 22, 345–356.

    Article  Google Scholar 

  18. Hwang, H, Moon, D.H and Shinn, S.W. (1990), “An E.O.Q. model with quantity discounts for both purchasing price and freight cost”, Computers & Operations. Research, 17(1), 73–78.

    Article  Google Scholar 

  19. Tersine, R.J and Toelle, R.A, (1985) “Lot size determination with quantity discounts”, Production and Inventory management, 27(3), 1–22.

    Google Scholar 

  20. Rubin, P.A, Dilts, D.M and Barron, B.M,(1983), “Economic order quantities with quantity discounts; Grandma does it best”, Decisions Sciences, 14, 270–281.

    Article  Google Scholar 

  21. Ghare, P.M and Schrader, G.F, (1963) “A model for exponential decaying inventory”, J. Ind. Eng ng, 14, 238–243.

    Google Scholar 

  22. Harris, F.W. (1915) “Operations and cost-factory management series”. A.W. Shaw Chicago. (Ch-4), 48–52.

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Kalyani, Pin- 741235, Kalyani, Nadia, West Bengal, India

    Manjusri Basu & Sudipta Sinha

Authors
  1. Manjusri Basu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sudipta Sinha
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Basu, M., Sinha, S. An ordering policy for deteriorating items with two component demand and price breaks allowing shortages. OPSEARCH 44, 51–72 (2007). https://doi.org/10.1007/BF03398791

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03398791

Keywords

Search

Navigation