Abstract
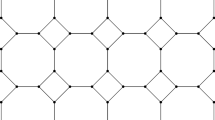
B.Grünbaum and G.C.Shephard could prove analogues of Kotzig’s theorem on minimal weights of edges for normal periodic tilings and mentioned that it is not hard to deduce from this that the graph of a normal periodic tiling cannot admit more than 13 pairwise edge-disjoint maximal matchings. We construct 13 pairwise edge-disjoint maximal matchings on the Laves-tiling [3.122] and prove that it is the only normal periodic tiling (up to combinatorial equivalence) with this property.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Literatur
B. Grünbaum, Convex Polytopes (Interscience, London, 1967).
B. Grünbaum, Matchings in Polytopal Graphs, Networks 4 (1974) 175–190.
B. Grünbaum und G.C. Shephard, Analogues for tilings of Kotzig’s theorem on minimal weights of edges, Ann. of Disc. Mathematics 12 (1982) 129–140.
B. Grünbaum und G.C. Shephard, Tilings and Patterns (Freeman, San Francisco, 1986).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Stehling, T. Paarweise kantendisjunkte maximale matchings in normalen periodischen Pflasterungen. Results. Math. 15, 179–185 (1989). https://doi.org/10.1007/BF03322454
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF03322454