Abstract
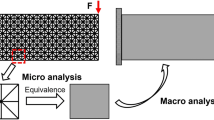
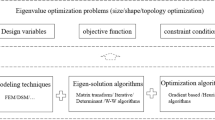
The homogenization method and the density function method are common approaches to evaluate the equivalent material properties for design cells composed of matter and void. In this research, using a new topology optimization method based on the homogenized material with a penalty factor and the chessboard prevention strategy, we obtain the optimal layout of a structure for the natural frequency of a designated mode. The volume fraction of nodes of each finite element is chosen as the design variable and a total material usage constraint is imposed. In this paper, the subspace method is used to evaluate the eigenvalue and its corresponding eigenvector of the structure for the designated mode and the recursive quadratic programming algorithm, PLBA algorithm, is used to solve the topology optimization problem.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bath, K. J., 1996,Finite Element Procedures, Prentice-Hall, New Jersey, pp. 954–978.
Bendsøe, M. P. and Kikuchi, N., 1988, “Generating Optimal Topologies in Structural Design Using A Homogenization Method,”Computer Methods in Applied Mechanics and Engineering, 71, pp. 197–224.
Bendsøe, M. P., Diaz, A. and Kikuchi, N., 1993,Topology Optimization of Structures, Kluwer Academic, Amsterdam, pp. 159–205.
Eshelby, J., 1957, “The Determination of The Elastic Field of An Ellipsoidal Inclusion, and Related Problem,”Processing of Royal Society, London, A241, pp. 379–396.
Gea, H. C., 1994, “Topology Optimization: A New Micro-Structure Based Design Domain Method,”ASME, Vol. 2, pp. 283–290.
Haug, E. J., Choi, K. K. and Komkov, V., 1986,Design Sensitivity Analysis of Structural Systems, Academic Press, London, pp. 49–70.
Jog, C. S., Haber, R. B. and Bendse, M. P., 1993,Topology Design of Structures, Kluwer Academic, Amsterdam, pp. 219–238.
Kawabe, Y. and Yoshida, S., 1994, “An Approach to The Problem of Vibration: Structural Modification by Optimizing Density Distribution,”ASME, Vol. 2, pp. 291–298.
Lim, O. K., 1985,An RQP Algorithm with Active Set Strategy for Optimum Design, Ph. D. Thesis, The University of Iowa, pp. 1–192.
Lim, O. K. and Lee, J. S., 1998, “Topology Optimization Using Equivalent Material Properties Prediction Techniques of Particulate-Reinforced Composites,”J. of The Computational Structural Engineering Institute of Korea, Vol. 42, No. 4, pp. 267–274. (In Korean)
Lim, O. K. and Lee, J. S., 1999, “Topology Optimization Using The Chessboard Prevention Strategy,”J. of The Computational Structural Engineering Institute of Korea., Vol. 12, No. 2, pp. 141–148. (In Korean)
Ma, Z. D., Kikuchi, N. and Hagiwara, I., 1993, “Structural topology and shape optimization for a frequency response problem,”Computational Mechanics, Vol. 13, pp. 157–174.
Mori, T. and Tanaka, K., 1973, “Average Stress in Matrix and Average Elastic Energy of Materials with Misfitting Inclusions,”ACTA Metallurgica, 21, pp. 571–574.
Park, S. H. and Youn, S. K., 1997a, “A Study on The Topology Optimization of Structures,”KSME Journal, Vol. 21, No. 8, pp. 1241–1249. (In Korean)
Sigmund, O., 1994,Design of Material Structures Using Topology Optimization, Ph. D. Thesis, Technical University of Denmark, pp. 70–85.
Yang, R. J. and Chuang, C. H., 1994, “Optimal Topology Design Using Linear Programming,”Computers & Structures, Vol. 52, No. 2, pp. 265–275.
Youn, S. K. and Park, S. H., 1997b, “A Study on The Shape Extraction Process in The Structural Topology Optimization Using Homogenized Material,”Computers & Structures, Vol. 62, No. 3, pp. 527–538.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lim, O.K., Lee, J.S. Structural topology optimization for the natural frequency of a designated mode. KSME International Journal 14, 306–313 (2000). https://doi.org/10.1007/BF03186423
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF03186423