Abstract
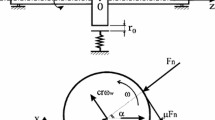
An analytical method is presented for evaluation of the steady state periodic behavior of nonlinear structural systems. This method is based on the substructure synthesis formulation and a harmonic balance procedure, which is applied to the analysis of nonlinear responses. A complex nonlinear system is divided into substructures, of which equations are approximately transformed to modal coordinates including nonlinear term under the reasonable procedure. Then, the equations are synthesized into the overall system and the nonlinear solution for the system is obtained. Based on the harmonic balance method, the proposed procedure reduces the size of large degrees-of-freedom problem in the solving nonlinear equations. Feasibility and advantages of the proposed method are illustrated using the study of the nonlinear rotating machine system as a large mechanical structure system. Results obtained are reported to be an efficient approach with respect to nonlinear response prediction when compared with other conventional methods.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Choi, Y. and Noah, S. T., 1987, “Nonlinear steady state response of a rotor-support system,”Trans. AS ME, Journal of Vibration, A coustics, Stress and Reliability in Design, Vol. 109, pp. 255–261.
Dokainish, M. A. and Subbaraj, K. 1989, “A Survey of Direct Time-Integration Methods in Computational Structural Dynamics,”Computers and Structures, Vol. 32, pp. 1371–1386.
Glisinn, D. E., 1982, “A High Order Generalized Method of Averaging,”SI AM Journal on Applied Mathematics, Vol. 42, No. 1, pp. 113–134.
Haquang, N. and Mook, D. T., 1987, “Non-linear Structural Vibration under Combined Parametric and External Excitation,”Journal of Sound and Vibration, Vol. 118-2, pp. 291–306.
Hassan A., 1994, “Use of Transformations with The Higher Order Method of Multiple Scales to Determine The Steady State Periodic Response of Harmonically Excited Non-linear oscillators, Part I: Transformation of Derivative,”Journal of Sound and Vibration, Vol. 178-1, pp. 1–19.
Iwatsubo Takuzo, Kawamura Shozo and Moon Byungyoung, 1998, “Non-Linear Vibration Analysis of Rotor System using Substructure Synthesis Method (Analysis with consideration of non-linearity of rotor),”JSME International Journal Series C, Vol. 41, No 4, pp 727–733.
Iwatsubo Takuzo, Shimbo Kenichi, Kawamura Shozo and Moon Byungyoung, 1999, “Non-Linear Vibration Analysis of Rotor System using Component Mode Synthesis Method (Proposition of construction method for the nonlinear restoring force term by using modal coordinates),”Trans. Jpn. Soc. Mech. Eng., (in Japanese) Series C, Vol. 65, No. 637, pp 3499–3506.
Moon Byungyoung, Kim Jin-Wook and Yang Bo-suk, 1999, “Non-Linear Vibration Analysis of Mechanical Structure System using Substructure Synthesis Method,”KSME International Journal, Vol. 13, No. 9, pp 620–629.
Moon Byungyoung and Kang Beom-soo, 2001, “Non-Linear Vibration Analysis of Mencnical System (Analysis with consideration of nonlinear sensitivity),”JSME International Journal Series C, Vol. 44, No. 1, pp. 12–20.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Moon, BY., Kang, BS. & Kim, BS. Dynamic analysis of harmonically excited non-linear structure system using harmonic balance method. KSME International Journal 15, 1507–1516 (2001). https://doi.org/10.1007/BF03185740
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF03185740