Abstract
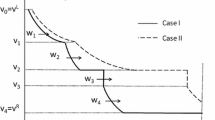
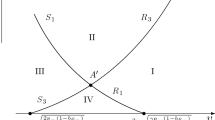
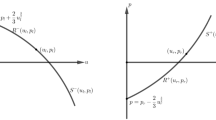
We are concerned with the Riemann problem ofp-system, i.e.,v t −u x =0,u t +p(v) x =0. We know that ifp is a monotone function, the solution can be constructed by shock waves and rarefaction waves. Therefore we consider the functionp which is not monotone. In this case, this system is a mixed type, and very little is known about this type of the system. Furthermore, we know that we can not construct the solution only by the above waves because of the ellipticity of the system. In order to overcome this difficulty, we consider the phase boundary, which is a shock wave with shock speed 0 and changes phases. Using this and the above waves, we describe the solution explicitly, for arbitrary initial step data.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
R. Courant and K.O. Friedrichs, Supersonic Flow and Shock Waves. Applied Mathematical Sciences21, Springer-Verlag, 1948.
H. Hattori, The Riemann Problem for a Van der Waals Fluid with Entropy Rate Admissibility Criterion-Isothermal Case. Arch. Rational Mech. Anal.,92 (1986), 247–263.
L. Leibovich, Solution of the Riemann problem for hyperbolic systems of quasilinear equations without convexity conditions. J. Math. Anal. Appl.,45 (1974), 81–90.
M. Shearer, The Riemann Problem for a Class of Conservation Laws of Mixed Type. J. Differential Equations,46 (1982), 426–443.
J. Smoller, Shock Waves and Reaction-Diffusion Equations. Grundlehren der mathematischen Wissenschaften258, Springer-Verlag, 1983.
B. Wendroff, The Riemann problem for materials with nonconvex equations of state 1: Isentropic flow. J. Math. Anal. Appl.,38 (1972), 81–90.
Author information
Authors and Affiliations
About this article
Cite this article
Yanagi, S. The Riemann problem for a class of conservation laws of van der waals fluid. Japan J. Indust. Appl. Math. 9, 239 (1992). https://doi.org/10.1007/BF03167567
Received:
Revised:
DOI: https://doi.org/10.1007/BF03167567