Skip to main content
SpringerLink
Log in

Numerical simulation of the droplet formation in a cross-junction microchannel using the Lattice Boltzmann Method

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

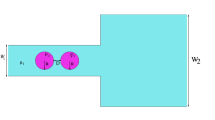
This study describes the numerical simulation of two-dimensional droplet formation and the following motion by using the Lattice Boltzmann Method (LBM) with the phase field equation. The free energy model is used to treat the interfacial force and the deformation of a binary fluid system, drawn into a cross-junction microchannel. While one fluid is introduced through the central inlet channel, the other fluid is drawn into the main channel through the two vertical inlet channels. Due to the effect of surface tension on the interface between the two fluids, the droplets of the first fluid are formed near the cross-junction. The aim in this investigation is to examine the applicability of LBM to the numerical analysis of the droplet formation and its motion in the microchannel. It was found from comparison with the experimentally visualized patterns that LBM with the free energy model can reproduce the droplet formation successfully. However because of the stability problem which is intrinsic for high surface-tension cases, it requires a very long computational time. This issue is to be resolved in the future.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

c :

Reference velocity

E :

Error

e :

Discrete particle velocity

F :

Free-energy function

f i :

Distribution function of the total density

f i :

Distribution function of the total density after the collision process

g i :

Distribution function of the density difference

g i :

Distribution function of the density difference after the collision process

P αβ :

Pressure tensor

Δt :

Time step

u :

Fluid velocity

U in :

Maximum velocity at the horizontal inlet

ũ j :

Normalized velocity

u j :

Normalized exact solution

V in :

Maximum velocity at the vertical inlet

Δx:

Space step

Γ:

Mobility coefficient of the fluids

Δμ:

Chemical potential difference

ξ:

Interfacial width

ρ:

Total density of both fluids

ρ a :

Density of fluid A

ρ b :

Density of fluid B

ρ *0 :

Reference density (dimensional)

σ:

Surface tension at the interface

ν:

Kinematic viscosity of both fluids

φ:

Density difference between fluid A and B

*:

Dimensional variable

eq:

Equilibrium term

a:

Fluid A

b:

Fluid B

i :

Link number

in:

Inlet

References

  • Gunstensen, A. K., Rothman, D. H., Zaleski, A. and Zanetti, G., 1991, “Lattice Boltzmann Model of Immiscible Fluid,”Physical Review A, Vol. 43, pp. 4320–4327.

    Article  Google Scholar 

  • Kim, K. C., Kim, J. M. and Yoon, S. Y., 2004, “Simultaneous Measurement of Internal and External Flow Fields around the Droplet Formation in a Microchannel,”4th KSV Conference, Korea, pp. 80–83.

  • Nourgaliev, R. R., Dinh, T. N., Theofanous, T. G. and Joseph, D., 2003, “The Lattice Boltzmann Equation method: Theoretical Interpretation, Numerics and Implications,”Multiphase Flows, Vol. 29, pp. 117–169.

    Article  Google Scholar 

  • Orlandini, E., Swift, M.R. and Yeomans, J. M., 1995, “A Lattice Boltzmann Model of Binary-Fluid Mixtures,”Europhysics Letters, Vol. 32, No. 6, pp. 463–468.

    Article  Google Scholar 

  • Qian, D. Y., 2003,Bubble Motion, Deformation and Breakup in Stirred Tanks, Ph.D. Dissertation, Clarkson University, USA.

    Google Scholar 

  • Shan, X. and Chen, H., 1993, “Lattice Boltzmann Model for Simulating Flows with Multiple Phases and Components,”Physical Review E, Vol. 47, pp. 1815–1819.

    Article  Google Scholar 

  • Succi, S., 2001,The Lattice Boltzmann Equation for fluid Dynamics and Beyond, Clarendon Press, Oxford

    Google Scholar 

  • Suh, Y. K. and Kang, S. M., 2006, “Assessment of Algorithms for the No-Slip Boundary Condition in the Lattice Boltzmann Method,” (submitted)

  • Sukop, M. C. and Thorne, D. T., 2006,Lattice Boltzmann Modeling, Springer, The Netherlands

    Google Scholar 

  • Swift, M. R., Orlandini, E., Osborn, W. R. and Yeomans, J. M., 1996, “Lattice Boltzmann Simulation of Liquid-Gas and Binary Fluid Systems,”Physical Review E, Vol. 54, No. 5, pp. 5041–5052.

    Article  Google Scholar 

  • Xu, A., Gonnella, G. and Lamura, A., 2003, “Phase-Separating Binary Fluids Under oscillatory Shear,”Physical Review E, Vol. 67, pp. 056105-1–056105-14.

    Google Scholar 

  • Xu, A., Gonnella, G. and Lamura, A., 2004, “Phase Separation of Incompressible Binary Fluids with Lattice Boltzmann Methods,”Physical A, Vol. 331, pp. 10–22.

    Article  Google Scholar 

  • Yu, D. Z., Mei, R. W., Luo, L. S. and Shyy, W., 2003, “Viscous Flow Computations with the Method of Lattice Boltzmann Equation,”Progress in Aerospace Sci., Vol. 39, pp. 329–367.

    Article  Google Scholar 

  • Yuan, P., 2005,Thermal lattice Boltzmann two-phase flow model for fluid dynamics, Ph.D. Dissertation, University of Pittsburgh, USA.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Dong-A University, 840 Hadandong, Sahagu, 604-714, Busan, Korea

    Zilu Li, Jinfen Kang, Jae Hyun Park & Yong Kweon Suh

Authors
  1. Zilu Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jinfen Kang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jae Hyun Park
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yong Kweon Suh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yong Kweon Suh.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, Z., Kang, J., Park, J.H. et al. Numerical simulation of the droplet formation in a cross-junction microchannel using the Lattice Boltzmann Method. J Mech Sci Technol 21, 162–173 (2007). https://doi.org/10.1007/BF03161722

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03161722

Key Words

Search

Navigation