Skip to main content
SpringerLink
Log in

Slow viscous flow past a cavity with infinite depth

  • Published:
Korean journal of computational & applied mathematics Aims and scope Submit manuscript

Abstract

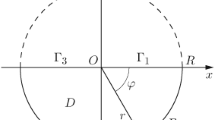
Two-dimensional slow viscous flow on infinite half-plane past a perpendicular infinite cavity is considered on the basis of the Stokes approximation. Using complex representation of the two-dimensional Stokes flow, the problem is reduced to solving a set of Fredholm integral equations of the second kind. The streamlines and the pressure and vorticity distribution on the wall are numerically determined.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. Imai.Ryutai Rikigaku (Fluid Dynamics), volume I. Shokabo, Tokyo, 1973.

    Google Scholar 

  2. J.W. Kim. 2-dimensional slow viscous flow past a cavity of semi-infinite depth. Master’s thesis, Department of Mathematics, KAIST, Korea, 1991.

    Google Scholar 

  3. M.-U. Kim. Slow viscous flow around a vertical fence on a plane.Journal of the Physical Society of Japan, 49(4):2387–2391, 1980.

    Article  MathSciNet  MATH  Google Scholar 

  4. M.-U. Kim, D.H. Choi, and J.T. Jeong. A two-dimensional model of a half-pitot tube.Fluid Dynamics Research, 5:135–145, 1989.

    Article  Google Scholar 

  5. M.-U. Kim and J.T. Jeong. Two-dimensional slow viscous flow due to the rotation of a body with cusped edges.Journal of the Physical Society of Japan, 59(9):3194–3202, 1990.

    Article  MathSciNet  Google Scholar 

  6. M.-U. Kim and C.H. Son. Two-dimensional slow viscous flow due to the motion of flat plate over a plane wall.Journal of the Physical Society of Japan, 50(4): 1392–1397, 1981.

    Article  Google Scholar 

  7. S. Richardson. Two-dimensional bubbles in slow viscous flows.Journal of Fluid Mechanics, 33(3):476–493, 1968.

    Article  MathSciNet  MATH  Google Scholar 

  8. M. Takematsu. Slow viscous flow past a cavity.Journal of the Physical Society of Japan, 21(9):1816–1821, 1966.

    Article  Google Scholar 

  9. R Teman.Navier-Stokes Equation. Amsterdam, 1979.

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Sunmoon University, 336-840, Asan, Chungnam, Korea

    D. W. Kim

  2. Department of Mathematics, Hannam University, 305-791, Taejon, Korea

    S. B. Kim

  3. Department of Mechanical Engineering, Korea Advanced Institute of Science & Technology, 305-701, Taejon, Korea

    J. H. Chu

Authors
  1. D. W. Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. B. Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. H. Chu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. W. Kim.

Additional information

supported by Hannam University Research Fund in 2000.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kim, D.W., Kim, S.B. & Chu, J.H. Slow viscous flow past a cavity with infinite depth. Korean J. Comput. & Appl. Math. 7, 569–580 (2000). https://doi.org/10.1007/BF03012269

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03012269

AMS Mathematics Subject Classification

Key word and phrases

Search

Navigation