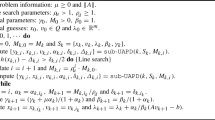Skip to main content
SpringerLink
Log in

The convergence of a dual algorithm for nonlinear programming

  • Published:
Korean journal of computational & applied mathematics Aims and scope Submit manuscript

Abstract

A dual algorithm based on the smooth function proposed by Polyak (1988) is constructed for solving nonlinear programming problems with inequality constraints. It generates a sequence of points converging locally to a Kuhn-Tucker point by solving an unconstrained minimizer of a smooth potential function with a parameter. We study the relationship between eigenvalues of the Hessian of this smooth potential function and the parameter, which is useful for analyzing the effectiveness of the dual algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. K. Arrow, L. Hurwicz and H. Dzava,Studies in Linear and Nonlinear Programming, Stanford University Press, Stanford, CA, 1958.

    Google Scholar 

  2. D. Bertsekas,A convergence analysis of the method of multipliers for nonconvex constrained optimization, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, 1978.

    Google Scholar 

  3. B. P. Bertsekas,Constrained Optimization and Lagrange Multiplier Methods, Academic Press, New York, 1982.

    MATH  Google Scholar 

  4. C. Charalambous,Nonliner least pth optimization and nonlinear programming, Math. Programming,12 (1977), 195–225.

    Article  MathSciNet  MATH  Google Scholar 

  5. A. S. El-Bakry, R. A. Tapia, T. Tsuchiya and Y. Zhang,On the fomulation and theory of the Newton interior-point method for nonlinear programming, Jornal of the Optimization Theory and Applications,89 (1996), 507–541.

    Article  MATH  Google Scholar 

  6. S.-P. Han,Superlinearly convergent variable metric algorithm for general nonlinear programming problems, Math. Programming,11 (1976), 263–282.

    Article  MathSciNet  MATH  Google Scholar 

  7. S.-p. Han,A global convergent method for nonlinear programming, Journal of the Optimization Theory and Applications,22 (1997), 297–309.

    Article  Google Scholar 

  8. Y.-Q. Hu,A Collection of Exercises in Operations Research, 2nd Edition, Tsinghua University Press, 1995.

  9. B. Kort and D. Bertsekas,A new penalty function for constrained minimization, Proc. IEEE Conference on Decision and Control, New Orleans, LA, 1972.

    Book  Google Scholar 

  10. X.-S. Li,An entropy-based aggregate method for minimax optimization, Eng. Optimization,18 (1992), 277–285.

    Article  Google Scholar 

  11. R. A. Polyak,Smooth optimization methods for minimax problems, SIAM J. Control and Optimization,26 (1988), 1274–1286.

    Article  MathSciNet  MATH  Google Scholar 

  12. H.-W. Tang and L.-W. Zhang,A maximum entropy method for linear programming, Chinese J. Num. Math. & Appli.,17:3 (1995), 54–65.

    MathSciNet  Google Scholar 

  13. H.-W. Tang and L.-W. Zhang,A maximum entropy method for convex programming, Chinese Science Bulletin,40:5 (1995), 361–364.

    MathSciNet  MATH  Google Scholar 

  14. A. B. Templeman and X.-S. Li,A maximum entropy approach to constrained nonlinear programming, Eng. Optimization,12 (1987), 191–205.

    Article  Google Scholar 

  15. H. Yamashita,A globally convergent primal-dual interior point method for constrained optimization, Technical Report, Mathmatical Systems Institute, Inc., Tokyo, Japan, 1992.

    Google Scholar 

  16. H. Yamashita and H. Yable,Superlinear and quadratic convergence of some primaldual interior point methods for constrained optimization, Math. Programming,75 (1996), 377–397.

    Article  MathSciNet  Google Scholar 

  17. H. Yable and H. Yamashita,Q-superlinear convergence of primal-dual interior point quasi-Newton methods for constrained optimization, Journal of the Operation Research Society of Japan,40 (1997), 415–436.

    Article  MathSciNet  MATH  Google Scholar 

  18. J. H. Wilkinson,The algebraic eigenvalue problem, Oxford, Clarendon, 1965.

    MATH  Google Scholar 

  19. L.-W. Zhang and H.-W. Tang,A maximum entropy algorithm with parameters for solving minimax problem, Archives of Control Sciences,6 (XIII) (1997), 47–59.

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Computational Mathematics and Scientific, Engineering Computing Chinese Academy of Sciences, P.O.Box 2719, 100080, Beijing, China

    Li-Wei Zhang

  2. Department of Applied Mathematics, Dalian University of Technology, 116024, Dalian, China

    Su-Xiang He

Authors
  1. Li-Wei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Su-Xiang He
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Li-Wei Zhang.

Additional information

Supported by the Science Foundation of DUT.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhang, LW., He, SX. The convergence of a dual algorithm for nonlinear programming. Korean J. Comput. & Appl. Math. 7, 487–506 (2000). https://doi.org/10.1007/BF03012264

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03012264

AMS Mathematics Subject Classification

Key word and phrases

Search

Navigation