Skip to main content
SpringerLink
Log in

Adaptive parallel decomposition for multidisciplinary design

  • Published:
KSME International Journal Aims and scope Submit manuscript

Abstract

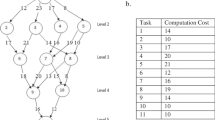
The conceptual design of a rotorcraft system involves many different analysis disciplines. The decomposition of such a system into several subsystems can make analysis and design more efficient in terms of the total computation time. Adaptive parallel decomposition makes the structure of the overall design problem suitable to apply the multidisciplinary design optimization methodologies and it can exploit parallel computing. This study proposes a decomposition method which adaptively determines the number and sequence of analyses in each sub-problem corresponding to the available number of processors in parallel. A rotorcraft design problem is solved and as a result, the adaptive parallel decomposition method shows better performance than other previous methods for the selected design problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

N:

The number of sub-problems

Nt:

The total number of analyses

pi :

Thei-th analysis module

pi k :

The z’-th analysis ink-th sub-problem

nk :

The number of analyses ink-th sub-problem

U, CL :

The amount of information transferred between sub-problems in upper and lower triangular regions

bk :

The sum of feedback couplings of thek-th sub-problem

References

  • Altus, S. S., KrI. M. and Gage, P. J. 1995, “A Genetic Algorithm for Scheduling and Decomposition of Multidisciplinary Design Problems,”Advances in design automation, ASME paper 95–141.

  • Gen, M. and Cheng, R. 1997,Genetic Algorithms and Engineering Design, pp. 234–248.

  • Kusiak. A. and Wang, J. 1993, “Decomposition of the Design Process,”ASME Journal of Mechanical Design, Vol. 115, pp. 687–695.

    Article  Google Scholar 

  • Michelena, N. F. and Papalambros, P. Y. 1994, “A Network Reliability Approach to Optimal Decomposition of Design Problems,”Advances in Design Automation, ASME, New York Vol. 2, pp. 195–204.

    Google Scholar 

  • Park. H. W., Kim, M. S., Choi, D. H. and Mavris, D. N., 2002, “Optimizing the Parallel Process Flow for the Individual Discipline Feasible Method,”9th AIAA/ISSMO Symposium and Exhibit on Multidisciplinary Analysis and Optimization, September 4–6.

  • Park, H. W., Kim, M. S., and Choi, D. H. 2003, “A System Decomposition Technique Using a Multi-Objective Genetic Algorithm.”KSME, Vol. 27. No. 4, pp. 499–506.

    MathSciNet  Google Scholar 

  • Park. H. W. 2003, “A Parallel Decomposition Method for Multidisciplinary Design Optimization Based on a Multiobjective Genetic Algorithm.” Ph. D. Thesis, Hanyang University, School of Mechanical Engineering.

  • Rogers, J. L. and Barthelemy, J. -F. M.. 1992, “Enhancements to the Design Manager's Aid for Intelligent Decomposition (DeMAID),”AIAA paper No. 92–4809.

  • Rogers. J. L.. and Bloebaum, L. 1994, “Ordering Design Tasks Based on Coupling Strength,”AIAA paper No. 94–4362.

  • Rogers, J. L., McCulley, M. and Bloebaum, L. 1999, “Optimizing the Process Flow for Complex Design Projects,”Design Optimkation: International Journal for Product & Process Improvement, Vol. 1, No. 3, pp. 281–292.

    Google Scholar 

  • Vanderplaats, G. N. 1995,DOT Users Manual Version 4.20, Vanderplaats Research & Development, Inc.

Download references

Author information

Authors and Affiliations

  1. R & D Division for Hyundai Motor Company, 772-1 Changduk-Dong, Hwasung-Si, Kynnggi-Do, Korea

    Hyung-Wook Park

  2. Department of Mechanical Engineering, The University of Seoul, 130- 743, Seoul, Korea

    Se J. Lee

  3. Research Assistant, the Center of Innovative Design Optimtation Technology, Hanyang University, 17 Haengdang-Dong, Sungdong-Gu, 133-791, Seoul, Korea

    Hyun-Seop Lee

  4. Center of Innovative Design Optimtation Technology, Hanyang University, 17 Haengdang-Dong, Sungdong-Gu, 133-791, Seoul, Korea

    Dong-Hoon Choi

Authors
  1. Hyung-Wook Park
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Se J. Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hyun-Seop Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Dong-Hoon Choi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dong-Hoon Choi.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Park, HW., Lee, S.J., Lee, HS. et al. Adaptive parallel decomposition for multidisciplinary design. KSME International Journal 18, 814–819 (2004). https://doi.org/10.1007/BF02990300

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02990300

Key Words

Search

Navigation