Skip to main content
SpringerLink
Log in

Vibrational characteristics of annular plates and rings of radially varying thinkness

  • Published:
KSME Journal Aims and scope Submit manuscript

Abstract

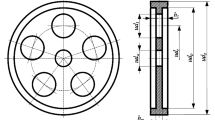
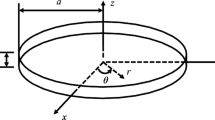
In this paper, annular plates having thickness variation are studied by deriving the equations of motion on the basis of the Mindlin plate theory. The Chebyshev collocation method is employed to solve the differential equation governing the transverse motion of such plates. The dimensionless frequencies are evaluated for different values of taper constant (α), thickness ratio (h u). radii ratio (ε) and power (n). The results of an experimental investigation are also presented, and the agreement between these findings and the predicted values in theory is remarkably good. As a result of this study, it is found that the effects of rotatory inertia and transverse shear deformation reduce the natural frequencies for all boundary conditions and for all values ofn. h o, ∈, a ands (mode number). This study also showed that the natural frequencies of annular plates with thickness expressed by the nth power function are higher than those by the (n−1)th power function for positive values of α, and vice versa for negative values ofe for all three boundary conditions. Moreover, there is a proof that the natural frequencies of annular plates tend to be higher as the taper constant decrease and/or as the radii ratio increase for all three boundary conditions and for all values ofn, s andh o.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

D :

Flexurai rigidity of plate *−Eh 3/12(1ν 2))

E :

Young’s modutus of annular plate

G :

Shear modulus of annular plate

H :

Dimensionless variable (−h/a)

K i :

Unknown constants

M r, Mθ :

Bending moments per unit length

M rθ :

Twisting moment per unit length

Q r, Qθ :

Radial and tangential shearing forces per unit length

T :

Chebyshes polynomials

T o :

Chebyshes polynomials with superseript meaning integration with respecty

a :

Outer radius

b :

Inner radius

h :

Thickness of plate defined by Eq. (5)

h o :

Thickness ratio

m :

Number of Chebyshev collocation point

n :

Power

q :

External force per unit area

s :

Mode number

t :

Time

x :

Dimensionless variable (−r/a)

y :

Chebyshev constant defined by Eq. (7b)

α:

Taper constant

ε:

Ratio of the inner and outer radin (b/a)

k :

Averaging shear coefficient (−π 2/12)

ν:

Poisson’s ratio

ϱ:

Density (mass per unit velume)

ω:

Circular frequency

Ω s :

Dimensionless frequency parameter including the effects of rotatory inertia

References

  • Bathe, K. J., 1982,Finite Element Procedures in Engineering Analysis, Prentice-Hall, Englewood Cliffs, N. J.

    Google Scholar 

  • Bathe, K. J., Brezzi, F. and Cho, S. W., 1989, “The MITC7 and MITC9 Plate Bending Elements.”Comp. Struct., Vol. 32, pp. 797–814.

    Article  MATH  Google Scholar 

  • Conway, H. D., 1958, “Some Special Solution for the Flexural Vibration of Disc of Varying Thickness,”Ingeniuer Archiv. Vol. 26, pp. 408–410.

    Article  MATH  MathSciNet  Google Scholar 

  • Dhatt, G. and Touzot, G., 1984,The Finite Element Method Displayed, John Wiley & Sons, New York.

    MATH  Google Scholar 

  • Gorman, D. G., 1983, “Natural Frequency of Transverse Vibration of Polar Orthotropic Variable Thickness Annular Plates,”J. Sound. Vibration, Vol. 86, pp. 47–60.

    Article  Google Scholar 

  • Harris, G. W., 1968, “The Normal Modes of a Circular Plate of Variable Thickness,”Quarterly Journal of Mechanics and Applied Mathematics, Vol. 21, pp. 322–327.

    Article  Google Scholar 

  • Hinton, E. and Huang, H. C., 1986, “A Family of Quadrilateral Mindlin Plate Elements with Substitute Shear Strain Fields”Comp. Struct., Vol. 23, pp. 409–431.

    Article  Google Scholar 

  • Kang, L. C., 1992, “A Fourier Series Method for Polygonal Domains; Large Element Computation for Plates,” Ph. D. Dissertation, Stanford University.

  • Lenox, T. A. and Conway, H. D., 1980, “An Exact Closed Form Solution for the Flexural Vibration of a Thin Annular Plate Having a Parabolic Thickness Variation,”J. Sound. Vibration., Vol. 68, pp. 231–239.

    Article  MATH  Google Scholar 

  • Leissa, A. W., 1969,Vibration of Plates, NASA, sp-100.

  • Mindlin, R. D., 1951, “Influence of Rotary Inertia on Flexural Motions of Isotropic, Elastic Plates,”J. Appl. Mech., Vol. 18, pp. 31–38.

    MATH  Google Scholar 

  • Prathap, G. and Babu, C. R., 1986, “A Field Consistent Three-noded Quadratic Curved Axisymmetric Shell Element,”Int. J. Numer. Methods Eng., Vol. 23, pp. 711–723.

    Article  MATH  MathSciNet  Google Scholar 

  • Ral, R. and Gupta, U. S., 1982, “Axisymmetric Vibration of Polar Orthotoropic Annular Plate of Variable Thickness,”J. Sound. Vib., Vol. 83, pp. 229–240.

    Article  Google Scholar 

  • Ramaiah, G. K. and Vijayakumar, K., 1985, “Vibration of Annular Plates with Linear Thickness Profiles,”J. Sound. Vib., Vol. 38, pp. 322–327.

    Google Scholar 

  • Soni, S. R. and Rao, L. A., 1975, “Axisymmetric Vibration of Annular Plates of Variable Thickness,”J. Sound. Vib., Vol. 38, pp. 465–473.

    Article  MATH  Google Scholar 

  • Vogel, S. M. and Skinner, D. W., 1965, “Natural Frequency of Transversely Vibrating Uniform Annular Plate,”J. Appl. Mech., Vol. 32 Dec. pp. 926–931.

    Google Scholar 

  • Zienkiewicz, O. C. and Taylor, R. L., 1991,The Finite Element Method, 4th edn, Vol. 2, McGraw-Hill.

Download references

Authors
  1. Seung -Ho Jang
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

College of Engineering Kyung Hee Univ.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jang, S.H. Vibrational characteristics of annular plates and rings of radially varying thinkness. KSME Journal 10, 146–157 (1996). https://doi.org/10.1007/BF02953654

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02953654

Key Words

Search

Navigation