Abstract
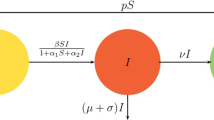
This work concerns the stabilization of uninfected steady state of an ordinary differential equation system modeling the interaction of the HIV virus and the immune system of the human body. The control variable is the drug dose, which, in turn, affects the rate of infection of CD4+ T cells by HIV virus. The feedback controller is constructed by a variant of the receding horizon control (RHC) method. Simulation results are discussed.
Similar content being viewed by others
References
A. Perelson, D. Kirschner and R. D. Boer,Dynamic of HIV infection of CD4 + T cells, Math. Biosc.114 (1993), 81–125.
D. Kirschner, S. Lenhart and S. Serbin,Optimal control of the chemotherapy of HIV, J. Math. Biol.35 (1997), 775–792.
K. R. Fister, S. Lenhart and J. S. McNally,Optimizing chemotherapy in an HIV model, Electronic J. of Diff. Eqs.1998 No 32 (1998), 1–12.
M. A. L. Caetano and T. Yoneyama,A comparative evaluation of open loop and closed loop drug administration strategies in the treatment of AIDS, Anais da Academia Brasileira de ciencias71 (1999), 589–597.
M. A. L. Caetano and T. Yoneyama,Short and long period optimization of drug doses in the treatment of AIDS, Anais da Academia Brasileira de ciencias74 (2002), 589–597.
D. Wodarz and M. A. Nowak,Mathematical models of HIV pathogenesis and treatment, BioEssays24 (2002), 1178–1187.
M. A. L. Caetano, J. A. M. Felippe de Souza and T. Yoneyama,A model based analysis of AIDS treatment, Proceeding of the Western Multiconference on Health Sciences Simulation, Orlando, USA (2003), 56–70.
Y. Huang, S. L. Rosenkranz and H. Wu,Modeling HIV dynamic and antiviral response with consideration of time-varying drug exposures, adherence and phenotypic sensitivity, Math. Biosc.184 (2003), 165–186.
S. Butler, D. Kirschner and S. Lenhart,Optimal control of the chemotherapy affecting the infectivity of HIV, Advances in Mathematical Population Dynamics-Molecules, Cell and Man, Editors: O. Arino, D. Axelrod and M. Kimmel, World Scientific press Singapore (1997), 557–569.
É. Gyurkovics,Receding horizon control via Bolza-type optimization, Syst. Control Lett.35 (1998), 195–200.
D. Q. Mayne, J. B. Rawlings, C. V. Rao and P. O. M. Scokaert,Constrained model predictive control: Stability and optimality, Automatica36 (2000), 789–814.
A. Jadababaie and J. Hauser,Inconstrained receding horizon control of nonlinear systems, IEEE Trans. Autom. Control46 (2001), 776–783.
K. Ito and K. Kunisch,A symptotic properties of receding horizon optimal control problems, SIAM J. of Control optim.40 (2002), 1585–1610.
D. Nešić, A. R. Teel and P. V. Kokotovic,Sufficient conditions for stabilization of sampled-data nonlinear systems via discrete-time approximation, Syst. Control Lett.38 (1999), 259–270.
D. Nešić and A. R. Teel,A framework for stabilization of nonlinear sampled-data systems based on their approximate discrete-time models, IEEE Trans. Autom. Control (2004) (to appear).
L. Grüne and D. Nešić,Optimization based stabilization of sampled-data nonlinear systems via their approximate discrete-time models, SIAM J. of Control Optim.42 (2003), 98–122.
A. M. Elaiw and É. Gyurkovics,Stabilizing receding horizon control of sampled-data nonlinear systems via their approximate discrete-time models. Proceedings of the 12th IFAC Workshop on Control Applications of Optimization, Visegrad, Hungary (2003), 65–61.
É. Gyurkovics and A. M. Elaiw,Stabilization of sampled-data nonlinear systems by receding horizon control via discrete-time approximation, Proceedings of the 2nd IFAC Conference on Control Systems Design, Bratislava Slovac Republic (2003).
M. Farkas,Dynamical models in biology, Academic press, 2001.
C. Jeffries, V. Klee and P. van den Driessche,Qualitative stability of linear systems, Linear Alg. and its Appl. (1987), 1–48.
N. Rouche, P. Habets and M. Laloy,Stability theory by Liapunov's direct method, Springer-Verlag, New York, 1977.
A. N. Michel and K. Wang,Qualitative theory of dynamical systems, Marcel Dekker, New York, 1995.
Author information
Authors and Affiliations
Corresponding author
Additional information
Ahmed Elaiw was born in Sohag, Egypt, in 1970. He received his B. Sc. degree in Mathematics from South Valley University, Sohag, Egypt in 1992, and his M. Sc. from Al-Azhar University, Cairo, Egypt, in 1997. He is currently Ph. D. student at the Budapest University of Technology and Economics, Institute of Mathemetics. His research interests include discrete-time, sampled-data and continuous-time nonlinear control systems, receding horizon control, application to HIV/AIDS models.
Krisztina Kiss received her Ph. D. at the University of Technology and Economics (Hungary) under the direction of Miklós Farkas. Since 1989 she has worked at the same University as an assistant professor. Her research interests focus on the dynamical models in biology.
Prof. Dr. Marco Antonio Leonel Caetano (Ibmec-São Paulo) Professor of Ibmec São Paulo of undergraduate studies and Master Business Administration (MBA). Graduated in Mathematics from Universidade Estadual Paulista (1987). Master in Aeronautics Engineering from Instituto Technologico da Aeronautica (1990), São Jose dos Campos, Brazil. Doctor in Aeronautics Engineering from Instituto Tecnolgico da Aeronautica (1996), São Jose dos Campos, Brazil. Member and Director of the SBA (Brazilian Automatic Society). He wrote around 50 academic papers and short articles on the applied mathematical studies. He also oriented several academic students in master and doctor degree.
Rights and permissions
About this article
Cite this article
Elaiw, A.M., Kiss, K. & Caetano, M.A.L. Stabilization of HIV/AIDS model by receding horizon control. JAMC 18, 95–112 (2005). https://doi.org/10.1007/BF02936558
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02936558