Skip to main content
SpringerLink
Log in

Bifurcations in a human migration model of Scheurle-Seydel type-II: Rotating waves

  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

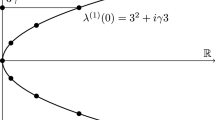
This paper treats the conditions for the existence of rotating wave solutions of a system modelling the behavior of students in graduate programs at neighbouring universities near each other which is a modified form of the model proposed by Scheurle and Seydel. We assume that both types of individuals are continuously distributed throughout a bounded two-dimension spatial domain of two types (circle and annulus), across whose boundaries there is no migration, and which simultaneously undergo simple (Fickian) diffusion. We will show that at a critical value of a system-parameter bifurcation takes place: a rotating wave solution arises.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. C. Alexander and J. F. G. Auchmuty,Global bifurcation of Waves, Manuscripta Mathematica27 (1979), 159–166.

    Article  MATH  MathSciNet  Google Scholar 

  2. J. F. G. Auchmuty,Bifurcating waves, Annals New York Academy of Sciences316 (1979), 263–278.

    Article  MathSciNet  Google Scholar 

  3. J. F. G. Auchmuty,Bifurcation analysis of reaction-diffusion equation v. rotating waves on a disc, in Fitzgibbon (ed), Partial Differential Equations and Dynamical Systems III (W. E. Pitman, Boston), (1984), 36–63.

    Google Scholar 

  4. P. C. Fife,Branching phenomena in fluid dynamics and chemical reaction-diffusion theory, Eigenvalues of non-linear problems (CIME lectures, Cremonese, Rome), (1974), 25–83.

    Google Scholar 

  5. M. Golubitsky, V. G. LeBlanc and I. Melbourne,Hopf Bifurcation from Rotating Waves and Patterns in Physical Space, J Nonlinear Sci.10, (2000) 69–101.

    Article  MATH  MathSciNet  Google Scholar 

  6. S. Kovács,Bifurcations in a human migration model of Scheurle-Seydel type—I: Turing bifurcation, International Journal of Bifurcation and Chaos13 5 (2003), 1303–1308.

    Article  MATH  MathSciNet  Google Scholar 

  7. J. Scheurle and R. Seydel,A model of student migration, International Journal of Bifurcation and Chaos10, 2 (2000) 477–480.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Numerical Analysis, Eötvös L. University, P. O. Box 32, H-1518, Budapest, Hungary

    Sándor Kovács

Authors
  1. Sándor Kovács
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sándor Kovács.

Additional information

Sándor Kovács began his studies at the Loránd Eötvös University (Bundapest) in 1988 and changed this for Ph. D course under the direction of Miklós Farkas in 1996. Since 1999 he theaches at the same university (Department of Numerical Analysis) and is a consultant at the Budapest University of Technology (Department of Differential Equations). His research interests focus on the bifurcation phenomena in biological systems and related topics.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kovács, S. Bifurcations in a human migration model of Scheurle-Seydel type-II: Rotating waves. JAMC 16, 69–78 (2004). https://doi.org/10.1007/BF02936151

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02936151

AMS Mathematics Subject Classification

Key words and phrases

Search

Navigation