Abstract
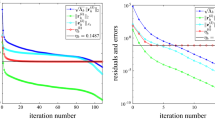
In each step of the quasi-minimal residual (QMR) method which uses a look-ahead variant of the nonsymmetric Lanczos process to generate basis vectors for the Krylov subspaces induced byA, it is necessary to decide whether to construct the Lanczos vectorsv n +1 andw n +1 as regular or inner vectors. For a regular step it is necessary thatD k =W T k V k is nonsingular. Therefore, in the floating-point arithmetic, the smallest singular value of matrix Dk,σ min (D k ), is computed and an inner step is performed ifσ min (D k )<∈, where ∈ is a suitably chosen tolerance. In practice it is absolutely impossible to choose correctly the value of the tolerance ∈. The subject of this paper is to show how discrete stochastic arithmetic remedies the problem of this tolerance, as well as the problem of the other tolerances which are needed in the other checks of the QMR method with the estimation of the accuracy of some intermediate results. Numerical examples are used to show the good numerical properties.
Similar content being viewed by others
References
M. Arioli, I. S. Duff and D. Ruiz,Stopping criteria for iterative solvers, SIAM J. Matrix Anal. Appl.13 (1992), 138–144.
J. M. Chesneaux,Study of the computing accuracy by using probabilistic approach, Contribution to Computer Arithmetic and Self Validating Numerical methods, IMACS, New Brunswick, NJ, (1990), 19–30.
J. M. Chesneaux,CADNA: An ADA tool for round-off errors analysis and for numerical debugging, Congress on ADA in Aerospace, Barcelon, (1990), 390–396
J. M. Chesneaux,Descriptif d'utilisation du logiciel CADNA-F, MASI Report, No. 92–32 (1992), 855–860.
J. M. Chesneaux,Stochastic arithmetic properties, Computational and Applied Mathematics, I-Algorithms and Theory, edited by C. Brezinski (North Holland, Amsterdam, 1992), 81–91.
J. M. Chesneaux and J. Vignes,Sur la robustesse de la méthode CESTAC, C. R. Acad. Sci. Paris, Sér. I, Math.307 (1988), 855–860.
J. M. Chesneaux and J. Vignes,Les fondements de l'arithmétique stochastique, C. R. Acad. Sci. Paris, Sér. I, Math.315 (1992), 1435–1440.
R. W. Freund, M. H. Gutknecht and N. M. Nachtigal,An implementation of the look-ahead Lanczos algorithm for non-Hermitian matrices, SIAM J. Sci. Comput.14 (1993), 137–158.
R. W. Freund and N. M. Nachtigal, QMR:a quasi-minimal residual method for non-Heritian linear systems, Numer. Math.60 (1991), 315–339.
R. W. Freund and T. Szeto,A transpose-free quasi-minimal residual squared algorithm for non-Heritian linear systems. In Advances in Computer Methods for Partial Differential Equations-VII, R. Vichnevetsky, D. Knight, and G. Richter, Eds. IMACS (1992), 258–264.
M. R. Hestenes and E. Stiefel,Methods of conjugate gradients for solving linear systems, J. Res. Natl. Bur. Stand49 (1952), 409–436.
B. N. Parlett,Reduction to tridiagonal form and minimal realizations, Preprint, Berkeley, January (1990), 409–436.
J. Vignes,Error analysis in computing, International Federation for Information Processing congress. Proceedings, Stockholm, (1974), 610–614
J. Vignes,New methods for evaluating the validity of the results of mathematical computations, Math. Comp. Simul, Vol.20 (1978), 227–249.
J. Vignes,Zéro mathématique et zéro informatique, C. R. Acad. Sci., Paris, sér I Math.303 (1986), 997–1000; also La Vie des Sciences4 (1987), 1–13.
J. Vignes,A stochastic arithmetic for reliable scientific computation, Math. Comp. Simul.35 (1993), 233–261.
J. Vignes,A stochastic approach to the analysis of round-off error propagation, A Survey of the CESTAC Method. Proceeding of Real Numbers and Computer Conference. Marseille, (1996), 233–251.
Author information
Authors and Affiliations
Corresponding author
Additional information
Faezeh Toutounian received her B. Sc in Mathematics from Ferdowsi University of Mashhad, Iran, two degree of M. Sc in Mathematical statistics and applied computer and her Ph. D in Mathematics from Paris VI University, France. She spent two sabbatical years in 1985 and 1996 at Paris VI University. She is currently a professor of Mathematics at Ferdowsi University of mashhad. Her research interests are mainly numerical linear algebra, iterative methods and error analysis.
Davod Khojasteh Salkuyeh received his B. Sc from Sharif University of Technology, Tehran, Iran and his M. Sc from Ferdowsi University of Mashhad, Mashhad, Iran. He received his Ph. D degree under supervision of professor Faezeh Toutounian at Ferdowsi University of Mashhad in 2003. He is currently an assistant professor of Mathematics at Mohaghegh Ardabili University of Ardabil, Iran. His research interests are mainly iterative methods for sparse linear systems and finite element method.
Bahram Asadi received his M. Sc degree under supervision of professor Faezeh Toutounian at Ferdowsi University of Mashhad, Iran. He is currently a lecturer in Islamic Azad Univrsity of Hamadan, Iran. His research interest is mainly iterative methods for sparse linear systems.
Rights and permissions
About this article
Cite this article
Toutounian, F., Salkuyeh, D.K. & Asadi, B. Numerical implementation of the QMR algorithm by using discrete stochastic arithmetic. JAMC 17, 457–473 (2005). https://doi.org/10.1007/BF02936068
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02936068