Abstract
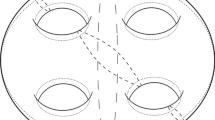
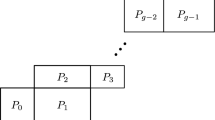
The purpose of this note is to study the π1 andH 1 systoles of two Riemann surfaces, the Klein genus 3 surface, y7 =x 2(1 −x), which we will denoteS K , and Bolza’s surface of genus 2,y 2 =x(1 −x 4), which we will denoteS B . Using period matrices, we identify theH 1 systoles and show for these examples that the π1 andH 1 systoles are in one-to-one correspondence. In their respective Teichmüller spaces,S B is known to be extremal andS K locally extremal for these systoles.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Baker, H. F.An Introduction to the Theory of Multiply Periodic Functions. Cambridge University Press, NY, 1907.
Barnes, E. S. The perfect and extreme senary forms.Canadian Journal of Mathematics,9, 235–242 (1957).
Beardon, A. F.The Geometry of Discrete Groups. Springer-Verlag, New York, 1983.
Bolza, O. On binary sextics with linear transformations into themselves.Amer. J. Math. 10, 47–60 (1888).
Buser, P., and Sarnak, P. On the period matrix of a Riemann surface of large genus (with an appendix by J. H. Conway and N. J. A. Sloane).Invent. Math. 117, 27–56 (1994).
Craig, M. Extreme forms and cyclotomy.Mathematika 25, 44–56 (1978).
Conway, J. H., and Sloane, N. J. A.Sphere Packings, Lattices and Groups. Springer-Verlag, 1988.
Conway, J. H., and Sloane, N. J. A. Low dimensional lattices III, perfect forms.Proc. R. Soc. Lond. A418, 43–80 (1988).
Earle, C. J., “H. E. Rauch, Function Theorist” inDifferential Geometry and Complex Analysis, I, (Chavel and H. M. Farkas eds.). Springer-Verlag, New York, 1985.
Elstrodt, J. Die Selbergsche Spurformel für kompacte Riemannsche Flächen.Jahrsber. Deutch. Math.-Verein 83, 45–77 (1981).
Gromov, M. Systoles and intersystolic inequalities, Actes de la Table Ronde de Géométrie Differentielle (Luming, 1992), 291–362, Semin. Congr., 1, Soc. Math. France, Paris, 1996.
Klein, F. Ueber die transformation siebenter Ordnung der elliptischen Functionen.Math. Ann. 25, 157–196 (1885).
Lang, S.Introduction to Algebraic and Abelian Functions. Springer-Verlag, 1982.
Mazur, B. Arithmetic on curves.Bull. Amer. Math. Soc. 14, 207–259 (1986).
McKean, H. P. Selberg’s trace formula as applied to a compact Riemann surface.Communications on Pure and Applied Mathematics 25, 225–246 (1972).
Rauch, H. E., and Lewittes, J. “The Riemann surface of Klein with 168 automorphisms” inProblems in Analysis, A Symposium in Honor of Solomon Bochner. Princeton University Press, Princeton, NJ, 1970.
Riera, G. Deformations of Klein’s curve and representations of its group of 168 automorphisms.Complex Variables 6, 265–281 (1986).
Riera, G., and Rodrigues, R. The period matrix of Bring’s curve.Pacific Journal of Mathematics 154, 179–200 (1992).
Schiller, J. Moduli for special Riemann surfaces of genus 2.Trans. Math. Math. Soc. 144, 95–113 (Oct. 1969).
Schmutz, P. Riemann surfaces with shortest geodesic of maximal length.Geometric and Functional Analysis 3, 564–631 (1993).
Weil, A. Sur les périodes des integrals abéliennes.Communications on Pure and Applied Mathematics 29, 813–819 (1976).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Quine, J.R. Systoles of two extremal Riemann surfaces. J Geom Anal 6, 461–474 (1996). https://doi.org/10.1007/BF02921661
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02921661