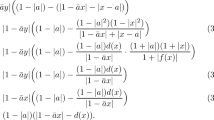Skip to main content
SpringerLink
Log in

Elliptic capacity and its distortion under conformal mapping

  • Published:
Journal d’Analyse Mathématique Aims and scope

Abstract

In 1947, Tsuji defined hyperbolic and elliptic versions of transfinite diameter of a closed set respectively in the unit disk and on the Riemann sphere, and gave least-energy descriptions. Duren and Pfaltzgraff recently found an extremal length description of hyperbolic capacity and used it to develop a hyperbolic version of Robin capacity similar that of Duren and Schiffer for the Euclidean metric. Tsuji used the chordal metric to define elliptic (or spherical) capacity, but this turns out to have been an unfortunate choice. An elliptic version of the theory is now developed with respect to the “pseudoelliptic metric”\([a, b] = \left| {\frac{{a - b}}{{1 + \bar ab}}} \right|\), previously used by Kühnau to define elliptic transfinite diameter of a closed “elliptically schlicht” subset of the sphere. An extremal length description is introduced, and an elliptic version of Robin capacity is developed and characterized by an extremal property of conformal mappings.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. L. V. Ahlfors,Conformal Invariants, McGraw-Hill, New York, 1973.

    MATH  Google Scholar 

  2. B. Dittmar and A. Yu. Solynin,Distortion of the hyperbolic Robin capacity under a conformal mapping, and extremal configurations, Zap. Nauchn. Sem POMI263 (2000), 49–69 (in Russian).

    Google Scholar 

  3. P. L. Duren,Univalent Functions, Springer-Verlag, New York, 1983.

    MATH  Google Scholar 

  4. P. Duren,Robin capacity, inComputational Methods and Function Theory (CMFT '97) (N. Papamichael, St. Ruscheweyh and E. B. Saff, eds.), World Scientific Publishing Co., Singapore, 1999, pp. 177–190.

    Google Scholar 

  5. P. Duren and J. Pfaltzgraff,Robin capacity and extremal length, J. Math. Anal. Appl.179 (1993), 110–119.

    Article  MathSciNet  MATH  Google Scholar 

  6. P. Duren and J. Pfaltzgraff,Hyperbolic capacity and its distortion under conformal mapping, J. Analyse Math.78 (1999), 205–218.

    Article  MathSciNet  MATH  Google Scholar 

  7. P. Duren, J. Pfaltzgraff and R. E. Thurman,Physical interpretation and further properties of Robin capacity, Algebra i Analiz9 (1997), no. 3, 211–219; St. Petersburg Math. J.9 (1998), 607–614.

    MathSciNet  Google Scholar 

  8. P. L. Duren and M. M. Schiffer,A variational method for functions schlicht in an annulus, Arch. Rational Mech. Anal.9 (1962), 260–272.

    Article  MathSciNet  MATH  Google Scholar 

  9. P. Duren and M. M. Schiffer,Robin functions and distortion of capacity under conformal mapping, Complex Variables Theory Appl.21 (1993), 189–196.

    MathSciNet  MATH  Google Scholar 

  10. G. M. Goluzin,Geometric Theory of Functions of a Complex Variable, second edition, Izdat. “Nauka”, Moscow, 1966; English translation: American Mathematical Society, Providence, Rhode Island, 1969.

    Google Scholar 

  11. F. Klein,Vorlesungen über nicht-euklidische Geometrie, Springer-Verlag, Berlin, 1928; reprinted 1968.

    MATH  Google Scholar 

  12. P. Koebe,Abhandlungen zur Theorie der konformen Abbildung, IV. Abbildung mehrfach zusammenhängender schlichter Bereiche auf Schlitzbereiche, Acta Math.41 (1918), 305–344.

    Article  MathSciNet  MATH  Google Scholar 

  13. R. Kühnau,Transfiniter Durchmesser, Kapazität und Tschebyschewsche Konstante in der euklidischen, hyperbolischen und elliptischen Geometrie, J. Reine Angew. Math.234 (1969), 216–220.

    MathSciNet  MATH  Google Scholar 

  14. R. Kühnau,Geometrie der konformen Abbildung auf der hyperbolischen und der elliptischen Ebene, VEB Deutscher Verlag der Wissenschaften, Berlin, 1974.

    MATH  Google Scholar 

  15. R. Kühnau,Variation of diametrically symmetric or elliptically schlicht conformal mappings. J. Analyse Math., this volume, pp. 303–316.

  16. M. Ohtsuka,Dirichlet Problem, Extremal Length and Prime Ends, Van Nostrand Reinhold, New York, 1970.

    MATH  Google Scholar 

  17. M. O'Neill and R. E. Thurman,Extremal domains for Robin capacity, Complex Variables Theory Appl.41 (2000), 91–109.

    MathSciNet  MATH  Google Scholar 

  18. R. E. Thurman,Upper bound for distortion of capacity under conformal mapping, Trans. Amer. Math. Soc.346 (1994), 605–616.

    Article  MathSciNet  MATH  Google Scholar 

  19. R. E. Thurman,Bridged extremal distance and maximal capacity, Pacific J. Math.176 (1996), 507–528.

    MathSciNet  Google Scholar 

  20. M. Tsuji,Some metrical theorems on Fuchsian groups. Japan. J. Math.19 (1947), 483–516.

    MathSciNet  Google Scholar 

  21. M. Tsuji,Potential Theory in Modern Function Theory, Maruzen, Tokyo, 1959.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Michigan, 48109-1109, Ann Arbor, MI, USA

    Peter Duren

  2. Fachbereich Mathematik, Martin-Luther-Universität, D-06099, Halle (Saale), Germany

    Reiner Kühnau

Authors
  1. Peter Duren
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Reiner Kühnau
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Peter Duren.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Duren, P., Kühnau, R. Elliptic capacity and its distortion under conformal mapping. J. Anal. Math. 89, 317–335 (2003). https://doi.org/10.1007/BF02893086

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02893086

Keywords

Search

Navigation