Abstract
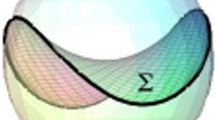
The behavior of wall-bound drops and bubbles is fundamental to many natural and industrial processes. Key characteristics of such capillary systems include interface shape and stability for a variety of gravity levels and orientations. Significant solutions are in hand for axisymmetric pendent drops for a variety of uniform boundary conditions along the contact line with gravity acting normal to a planar wall. The special case of a wall-bound drop or bubble that is also pinned at an edge (i.e. a ‘wall-edge-bound’ drop) is considered here where numerical solutions are obtained for interface shape and stability as functions of drop volume, contact angle, fluid properties, and uniform gravity vector. For a semi-infinite zero-thickness planar wall (plate), a critical contact angle is identified below which wall-edge-bound drops are always stable. The critical contact angle is computed as a function of the gravity vector. The numerical procedure, which makes no account for contact angle hysteresis, predicts that such wall-edge-bound drops are unconditionally unstable for any gravity field with a component that is tangent to the wall while inwardly normal to the edge. Select experiments are conducted that support the conclusions drawn from the numerical results.
Similar content being viewed by others
References
D. C. Dyson. Contact line stability at edges: Comments on Gibbs’s inequalities. Physics of Fluids, 31(2):229–232, February 1988.
J. F. Oliver, C. Huh, andS. G. Mason. Resistance of spreading of liquids by sharp edges. Journal of Colloid and Interface Science, 59(3):568–581, May 1977.
L. R. White. The equilibrium of a liquid drop on a nonhorizontal substrate and the Gibbs’s criteria for advance over a sharp edge. Journal of Colloid and Interface Science, 73(1):256–259, January 1980.
K. A. Brakke. The Surface Evolver. Experimental Mathematics, 1:141–165, 1992. The manual and code are available at http://www.susqu.edu/facstaff/b/brakke/.
S. H. Collicott andM. M. Weislogel. Computing existence and stability of capillary surfaces using surface evolver. AIAA Journal, 42(2):289–295, February 2004.
K. A. Brakke. The Surface Evolver and the stability of liquid surfaces. Phil. trans. R. Soc. Lond, A, 354:2143–2157, 1996.
E. B. Dussan V. Hydrodynamic stability and instability of fluid systems with interfaces. Arch. Rat. Mech. Anal., 57(4):364–379, 1975.
M. M. Weislogel and H. D. Ross. Surface settling in partially filled containers upon step reduction in gravity. Technical Memorandum 103641, NASA, 1990.
D. Langbein. Capillary Surfaces: Shape-Stability-Dynamics, in Particular Under Weightlessness. Number 178 in Springer Tracts in Modern Physics. Springer, 2001. Chapter 4.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Chen, Y., Bacich, M., Nardin, C. et al. The shape and stability of wall-bound and wall-edge-bound drops and bubbles. Microgravity sci. Technol. 17, 14–24 (2005). https://doi.org/10.1007/BF02889516
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF02889516