Skip to main content
SpringerLink
Log in

Chaos behavior in the discrete Fitzhugh nerve system

  • Published:
Science in China Series A: Mathematics Aims and scope Submit manuscript

Abstract

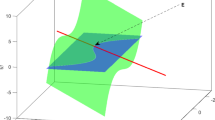
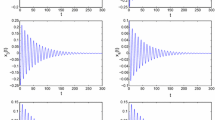
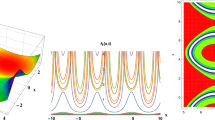
The discrete Fitzhugh nerve systems obtained by the Euler method is investigated and it is proved that there exist chaotic phenomena in the sense of Marotto’s definition of chaos. And numerical simulations not only show the consistence with the theoretical analysis but also exhibit the complex dynarnical behaviors, including the ten-periodic orbit, a cascade of period-doubling bifurcation, quasiperiodic orbits and the chaotic orbits and intermittent chaos. The computations of Lyapunov exponents confirm the chaos behaviors. Moreover we also find a strange attractor having the self-similar ohit structure as that of Henon attractor.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Hodgin, A. L., A. F., Huxley, A quantitative description of membrane current and its application to conduction and excitation on nerve, J. Physiol., 1952, 117:500–544.

    Google Scholar 

  2. Fitzhugh, R., Impulses and physiological states in theoretical models of nerve membrane, Biophysical J., 1961, 1: 445–466.

    Article  Google Scholar 

  3. Kaumann, K., Staude, U., Uniqueness and nonexistence of limit cycles for the FitzHugh equation, Equadiff 82 ( eds. Knobloch, H. W., Schmitt, K.), Lecture Notes in Math., Vol. 1017, New York: Springer-Verlag, 1983, 313–321.

    Google Scholar 

  4. Treskov, S. A., Volokitin, E. P., On existence of periodic orbits for the FitzHugh nerve system, Quart. Appl. Maths., 1996; LIV: 601–607.

    MathSciNet  Google Scholar 

  5. Sugie, J. Nonexistence of periodic solutions for the FitzHugh nerve system, Quart. Appl. Math., 1991,49: 543–554.

    MATH  MathSciNet  Google Scholar 

  6. Braaksma, B., Grasman, J.,Critical dynamics of the Bonhoeffer-van der Pol equation and its chaotic response to periodic stimulation. Physica D, 1993, 68: 265–280.

    Article  MATH  MathSciNet  Google Scholar 

  7. Rajasekar, S., Lakshmanan, M., Algorithms for controlling chaotic motion: application for the BVP oscillator, Physica, 1993,67D: 282–300.

    Google Scholar 

  8. Rajasekar, S., Parthasarathy, S., Lakshmanan, M., Prediction of horseshoe chaos in BVP and DVP oscillators, Chaos, Soliton and Fractals, 1992, 2: 2712gb-280.

    MathSciNet  Google Scholar 

  9. Ott, E., Chaos in Dynamical Systems, Cambridge: Cambridge University Press, 1993.

    MATH  Google Scholar 

  10. Marotto, F. R.,Snapback repellers imply chaos in Rn, J. Mathematical Analysis and Applications, 1978, 63: 199–223.

    Article  MATH  MathSciNet  Google Scholar 

  11. Wiggins, S.,An Introduction to Applied Nonlinear Dynamics and Chaos, New York: Springer-Verlag, 1990.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Hunan Normal University, 410081, Changsha, China

    Zhujun Jing & Yu Chang

  2. Institute of Mathematics, Academy of Mathematics and System Sciences, Chinese Academy of Sciences, 100080, Beijing, China

    Zhujun Jing

  3. lnstitute of Applied Mathematics, Academy of Mathematics and System Sciences, Chinese Academy of Sciences, 100080, Beijing, China

    Zhiyuan Jia

Authors
  1. Zhujun Jing
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhiyuan Jia
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yu Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhujun Jing.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jing, Z., Jia, Z. & Chang, Y. Chaos behavior in the discrete Fitzhugh nerve system. Sci. China Ser. A-Math. 44, 1571–1578 (2001). https://doi.org/10.1007/BF02880796

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02880796

Keywords

Search

Navigation