Abstract
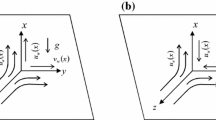
The effect of surface mass transfer velocities having normal, principal and transverse direction components (‘vectored’ suction and injection) on the steady, laminar, compressible boundary layer at a three-dimensional stagnation point has been investigated both for nodal and saddle points of attachment. The similarity solutions of the boundary layer equations were obtained numerically by the method of parametric differentiation. The principal and transverse direction surface mass transfer velocities significantly affect the skin friction (both in the principal and transverse directions) and the heat transfer. Also the inadequacy of assuming a linear viscosity-temperature relation at low-wall temperatures is shown.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Abbreviations
- a, b:
-
velocity gradients inx andy directions, respectively
- c:
-
ratio of velocity gradients,b/a
- Cfx, Cfy :
-
skin-friction coefficients alongx andy directions, respectively
- f, s:
-
dimenionless stream functions such thatf′=u/u e ands′=v/v e
- fw :
-
mass transfer parameter,-(ρw) w/(ρeμea)1/2
- g:
-
dimensionless enthalpy,h/h e
- gw :
-
cooling parameter for the wall,h w/he
- h:
-
enthalpy
- Pr:
-
Prandtl number
- q:
-
heat transfer rate
- Rex :
-
local Reynolds number,u cx/ve
- St:
-
Stanton number
- T:
-
temperature
- u, v, w:
-
velocity components alongx, y, z directions, respectively
- x, y, z:
-
principal, transverse and normal directions, respectively
- η:
-
similarity variable, (ρ e /μ e )1/2 ∫ z0 (ρ/ρ e )dz
- μ:
-
coefficient of viscosity
- ν:
-
kinematic viscosity
- ρ:
-
density
- τx, τy :
-
dimensional shear stress functions
- ω:
-
exponent in the power-law variation of viscosity
- ′ (prime):
-
differentiation with respect toη
- e:
-
condition at the edge of the boundary layer
- w:
-
condition at the surfacez=η=0.
References
Ackroyd J A D 1970Aeronaut. J. 74 155
Bourne D E and Elliston D G 1970Int. J. Heat Mass Transfer 13 583
Gross J F and Dewey C F 1965Fluid Dynamics Trans. ed. W Fiszdon (Pergamon Press) Vol. 2, p. 529
Inger G R and Swean T F 1975AIAA J. 13 616
Libby P A 1967AIAA J. 5 507
Libby PA 1974AIAA J. 12 408
Na T Y and Turski C E 1974Aeronaut. Q. 23 14
Nath G and Muthanna M 1976AIAA J. 14 1777
Rubbert P E 1965 Ph.D. Thesis M.I.T. Cambridge
Rubbert P E and Landahl M T 1967Phys. Fluids 10 831
Sakiadis B C 1961A.I. Ch. E.J. 7 26–28, 221–225, 467–472
Scala S and Sutton G 1957Jet Propulsion 27 895
Tan C W and DiBiano R 1972AIAA J. 10 923
Vimala C S and Nath G 1975AIAA J. 13 711
Williams J C and Johnson W D 1974AIAA J. 12 1427
Wortman A, Zeigler H and Soo-Hoo G 1971Int. J. Heat Mass Transfer 14 149
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Muthanna, M., Nath, G. Laminar compressible boundary layer flow at a three-dimensional stagnation point with vectored mass transfer. Proc. Indian Acad. Sci. (Math. Sci.) 87, 113–123 (1978). https://doi.org/10.1007/BF02837706
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02837706