Skip to main content
SpringerLink
Log in

The equitable total chromatic number of the graphHM(W n )

  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

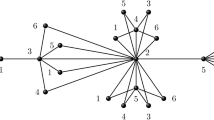
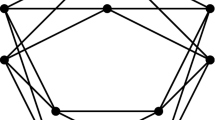
Abstract

The equitable total chromatic number Χet (G) of a graphG is the smallest integerk for whichG has a total k-coloring such that the number of vertices and edges in any two color classes differ by at most one. In this paper, we determine the equitable total chromatic number of one class of the graphs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bor-liang Chen and Ko-wei Lih,Equitable coloring of trees, Journal of Combnatorial Theory, Series B61 (1994), 83–87.

    Article  MATH  MathSciNet  Google Scholar 

  2. Bor-liang Chen, Ko-wei Lih and Pou-lin Wu,Equitable coloring and the maximum degree, European Journal of Combinatorics15 (1994), 443–447.

    Article  MATH  MathSciNet  Google Scholar 

  3. Hung-lin Fu,Some results on equalized total coloring, Congressus Numerantium102 (1994), 111–119.

    MATH  MathSciNet  Google Scholar 

  4. Ko-wei Lih and Pou-lin Wu,On equitable coloring of bipartite graphs, Discrete Mathematics151 (1996), 155–160.

    Article  MATH  MathSciNet  Google Scholar 

  5. Walter Meyer,Equitable coloring, American Mathematical Monthly80 (1973), 920–922.

    Article  MATH  MathSciNet  Google Scholar 

  6. Wei-fan Wang,Equitable Total Coloring of Graphs with Maximum Degree 3, Graphs and Combinatorics18 (2002), 677–685.

    Article  MATH  MathSciNet  Google Scholar 

  7. Hai-ying Wang and Liang Sun,Equitable total chromatic numbers of Mycielski graphs of two classes of graphs, Science & Technology Review206 (2005), 29–30.

    Google Scholar 

  8. Zhong-fu Zhang,On the equitable total chromatic number of Mycielski graphs of Cycles Cn, Journal of LanZhou Railway University22 (2003), 1–3.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Beijing Institute of Technology, 100081, Beijing, P. R. China

    Haiying Wang

  2. School of Mathematics and Information, Yantai Normal University, 264025, Yantai, P. R. China

    Jianxin Wei

Authors
  1. Haiying Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jianxin Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Haiying Wang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, H., Wei, J. The equitable total chromatic number of the graphHM(W n ). J. Appl. Math. Comput. 24, 313–323 (2007). https://doi.org/10.1007/BF02832320

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02832320

AMS Mathematics Subject Classification

Key words and phrases

Search

Navigation