Abstract
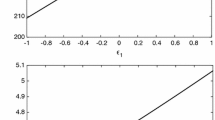
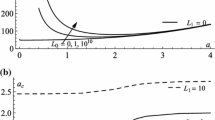
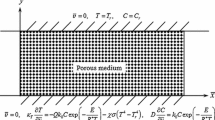
The problem of the convective instability of a plane fluid layer bounded by rigid walls with heating in a narrow layer running parallel to the walls inside the volume in question is solved. Instability criteria depending on the location of the heated layer and the Rayleigh numbers of the upper and lower layers are found. The results are compared with those for a plane layer with uniform energy release inside the volume.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. Chandrasekhar,Hydrodynamic and Hydromagnetic Stability, Clarendon Press, Oxford (1961).
G. Z. Gershuni and E. M. Zhukhovitskii,Convective Stability of an Incompressible Liquid [in Russian], Nauka, Moscow (1972).
E. M. Sparrow, R. J. Goldstein, and V. K. Jonsson, "Thermal instability in a horizontal fluid layer: effect of boundary conditions and non-linear temperature profile,J. Fluid Mech.,18, 513 (1964).
G. Z. Gershuni, E. M. Zhukhovitskii, and A. A. Nepomnyashchii,Stability of Convective Flows [in Russian], Nauka, Moscow (1989).
D. R. Jones, "The dynamic stability of confined, exothermically reacting fluids,"Intern. J. Heat and Mass Transfer,16, 157 (1973).
A. V. Uvarov, A. I. Osipov, S. A. Pilipyuk, and A. I. Sokolov, "Convective instability of a nonequilibrium gas,"Khim. Fiz.,13, No. 8–9, 217 (1994).
J. Ullenbusch, "High-pressure continuous optical discharges," in:Invited Papers 16th Intern. Conf. Phenom. Ionized Gases, Sept. Inst. Theoret. Phys., Dusseldorf (1983), p. 119.
G. Z. Gershuni and E. M. Zhukhovitskii, "Instability of a system of horizontal immiscible liquid layers with heating from above,"Izv. Akad. Nauk USSR, Mekh. Zhidk. Gaza, No. 6, 28 (1980).
G. Z. Gershuni and E. M. Zhukhovitskii, "Monotonic and vibrational instability of a two-layer system of immiscible liquids with heating from below,"Dokl. Akad. Nauk USSR,265, 302 (1982).
A. A. Nepomnyashchii and I. B. Simanovskii, "Onset of convection with heating from above and heat release on an interface,"Izv. Akad. Nauk USSR, Mekh. Zhidk. Gaza, No. 3, 16 (1990).
A. Pellew and R. V. Southwell, "On maintained convective motion in a fluid heated from below,"Proc. Roy. Soc. London, Ser. A.,176, No. 966, 312 (1940).
V. S. Sorokin, "The variational method in the theory of convection,"Prikl. Mat. Mekh.,17, 39 (1953).
Additional information
Moscow. Translated from Izvestiya Rossiiskoi Akademii Nauk, Mekhanika Zhidkosti i Gaza, No. 1, pp. 8–15, January–February, 1997.
The work was carried out with partial support from the Russian Foundation for Fundamental Research (project No. 95-01-00354a).
Rights and permissions
About this article
Cite this article
Vetyukov, A.A., Osipov, A.I. & Uvarov, A.V. Convective instability in the presence of volume energy release. Fluid Dyn 32, 5–10 (1997). https://doi.org/10.1007/BF02697930
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02697930