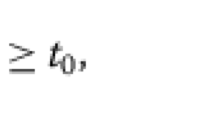Abstract
Oscillation criteria for the first order differential equation with deviating argumentsx′(t)+p(t)x(t−τ(t))==0,t≥t 0 are established in the case where {fx297-1}
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
G. Ladas, V. Lakshmikantham, J.S. Papadakis. Oscillation of Higher-order Retarded Differential Equations Generated by the Retarded Arguments. Delay and Functional Differential Equations and their Applications. Academic Press, New York and London, 1972, 219–231
G. Ladas. Sharp Conditions for Oscillations Caused by Delays.Appl. Anal., 1979, 9: 93–98
R.G. Koplatadze, T.A. Chanturija. On Oscillatory and Monotonic Arguments.Differencial'nye Uravnenija, 1982, 18: 1463–1465 (in Russian)
G.S. Ladde, V. Lakshmikantham, B.G. Zhang. Oscillation Theory of Differential Equations with Deviating Arguments. Marcel Dekker, New York, 1987
L.H. Erbe, B.G. Zhang. Oscillation for First Order Linear Differential Equation with Deviating Arguments.Differential Integral Equations, 1988, 1: 305–314
A. Elbert, I.P. Stavroulakis. Oscillations of First Order Differential Equations with Deviating Arguments. Recent Trends in Differential Equations, 163–178, World Sci. Ser. Appl. Anal., 1, World Sci. Publishing Co., 1992
R. Koplatadze, G. Kvinikadze. On the Oscillation of Solutions of First Order Delay Differential Inequaties and Equations.Georgian Math. J., 1994, 1(6): 675–685
M.K. Kwong. Oscillation of First-order Delay Equations.J. Math. Anal. Appl., 1991, 156: 274–286
J.S. Yu, Z.C. Wang. Some Further Results on Oscillation of Neutral Differential Equations.Bull. Austral. Math. Soc., 1992, 46: 149–157
A. Elbert, I.P. Stavroulakis. Oscillation and Non-oscillation Criteria for Delay Differential Equations.Proc. Amer. Math. Soc., 1995, 123: 1503–1510
Author information
Authors and Affiliations
Additional information
This project is supported by the National Natural Sciences Foundation of China and Natural Sciences Foundation of Human Province.
Rights and permissions
About this article
Cite this article
Yong, Z., Yuanhong, Y. On the oscillation of solutions of first order differential equations with deviating arguments. Acta Mathematicae Applicatae Sinica 15, 297–302 (1999). https://doi.org/10.1007/BF02669834
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02669834