Abstract
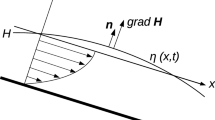
A boundary element method has been developed for analysing heat transport phenomena in solitary wave on falling thin liquid films at high Reynolds numbers. The divergence theorem is applied to the non-linear convective volume integral of the boundary element formulation with the pressure penalty function. Consequently, velocity and temperature gradients are eliminated, and the complete formulation is written in terms of velocity and temperature. This provides considerable reduction in storage and computational requirements while improving accuracy. The non-linear equation systems of boundary element discretization are solved by the quasi-Newton iterative scheme with Broyden’s update. The streamline maps and the temperature distributions in solitary wave and wavy film flow have been obtained, and the variations of Nusselt numbers along the wall-liquid interface are also given. There are large cross-flow velocities and S-shape temperature distributions in the recirculating region of solitary wave. This special flow and thermal process can be a mechanism to enhance heat transport.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Zabaras, G.T., et al., “Vertical Upward Cocurrent Gas-Liquid Annular Flow”AIChE J. 32, No.5, pp.829, (1986).
Cai, X.-S., Xu, A.-Q., Tong, Z.-M., “Experimental Study of Solitary Waves on Falling Film” Proceedings of 2nd International Symposium on Multiphase Flow and Heat Transfer,1, pp.183–188, Hemisphere (1989).
Wasden, F.K., Dukler, A.E., “Insights into the Hydrodynamics of Free Falling Wavy Films,”AIChE J. 35, No.2, pp.187–195, (1989).
Bach, P., Villadsen, J., “Simulation of the Vertical Flow of a Thin Wavy Film Using a Finite Element Method,”Int. J. Heat Mass Transfer,27, pp.815, (1984).
Kheshgi, H.S., Scriven, L.E., “Disturbed Film Flow on a Vertical Plate,”Phy. Fluids,30, pp.990, (1987).
Leonard, B.P., “A Stable and Accurate Convective Modelling Procedure Based on Quadratic Upstream Interpolation,”Comp. Math. Appl. Mech. Eng.,12, p.59, (1979).
Pollard, S.V., Siu, A.L.W., “The Calculation of Some Laminar Flows Using Various Discretization Schemes,”Comp. Math. Appl. Mech. Eng.,35, p.293, (1982).
Kitagawa, K., Brebbia, C.A., Wrobel, L.C., Tanaka, M., “Boundary Element Analysis of Viscous Flow by Penalty Function Formulation,”Engineering analysis,3, No.4, pp.194–200, (1986).
Lu, W.-Q, «Boundary Element Method of Analysing Non-Linear Phenomena on Gas-Liquid Two-Phase Free Surface at Middle and Higher Reynolds Numbers», Computational Modelling of Free Surfac and Moving Boundary Problems II, pp. 167–176, edited by Wrobel, L.C. and Brebbia, C.A., Computational Mechanics Publictions, (1993).
Lu, W.-Q., “Simulation of Thermocapillary Convection in a Two-Layer Immiscible Fluid System Using a Boundary Element Method,”Journal of Thermal Science,1, No.4, pp.259–266, (1992).
Lu, W.-Q., Chang, H.-C., “An Extension of the Biharmonic Boundary Integral Method to Free Surface Flow in Channels,”Journal of Computational Physics,77, No.2, pp.340–360, (1988).
Lu, W.-Q., «Boundary Element Analysis of Free Surface Problems of Axisymmetric Taylor Bubbles», Boundary Elements XII,2, pp.131–143, edited by Brebbia, C.A., Springer-verlag, (1990).
Dennis, J.E., More, J., “Quasi-Newton Methods, Motivation and Theory,”SIAM Rev.,19, pp.46–89, (1977).
Cuvelier, C., Driessen, J.M., “Thermocapillary Free Boundaries in Crystal Growth,”J. Fluid Mech. 169, pp.1–26, (1986).
Author information
Authors and Affiliations
Additional information
This project was financially supported by the National Natural Science Foundation of China
Rights and permissions
About this article
Cite this article
Lu, WQ. Numerical simulation using boundary element method of the mechanism to enhance heat transport by solitary wave on falling thin liquid films. J. of Thermal Science 2, 196–204 (1993). https://doi.org/10.1007/BF02650857
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02650857