Skip to main content
SpringerLink
Log in

Largest digraphs contained in alln-tournaments

  • Published:
Combinatorica Aims and scope Submit manuscript

Abstract

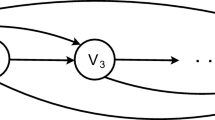
Letf(n) (resp.g(n)) be the largestm such that there is a digraph (resp. a spanning weakly connected digraph) onn-vertices andm edges which is a subgraph of every tournament onn-vertices. We prove that

$$n\log _2 n - c_1 n \geqq f(n) \geqq g(n) \geqq n\log _2 n - c_2 n\log \log n.$$

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. B. Alspach andM. Rosenfeld, Realization of certain generalized paths in tournaments,Discr. Math. 34 199–202.

  2. P. Erdős andL. Moser, On the representation of directed graphs as unions of orderings,Publ. Math. Inst. Hungar. Acad. Sci. 9 (1964), 125–132.

    Google Scholar 

  3. R. Forcade, Parity of paths and circuits in tournaments,Discr. Math. 6 (1973), 115–118.

    Article  MATH  MathSciNet  Google Scholar 

  4. B. Grünbaum, Antidirected Hamiltonian Paths in tournaments,J. Combinatorial Theory (B) 11 (1971), 249–257.

    Article  MATH  Google Scholar 

  5. H. G. Landau, On dominance relations and the structure of animal societies, III; the condition for a score structure,Bull. Math. Biophys. 15 (1955), 143–148.

    Article  Google Scholar 

  6. J. W. Moon,Topics on tournaments, Holt, Rinehart and Winston, New York, 1968.

    MATH  Google Scholar 

  7. L. Rédei, Ein Kombinatorischer Satz,Acta Sci. Math. (Szeged) 7 (1934), 39–43.

    MATH  Google Scholar 

  8. M. Rosenfeld, Antidirected Hamiltonian Circuits in tournaments,J. Combinatorial Theory (B) 16 (1974), 234–242.

    Article  MATH  MathSciNet  Google Scholar 

  9. M. Saks andV. T. Sóss, On unavoidable subgraphs of tournaments, to appear.

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics and Computer Science Hebrew University, 91904, Jerusalem, Israel

    N. Linial

  2. Department of Mathematics, Rutgers University, 08903, New Brunswick, N. J., USA

    M. Saks

  3. Department of Analysis I., Eötvös University, H-1088, Budapest, Hungary

    Vera T. Sós

Authors
  1. N. Linial
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Saks
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Vera T. Sós
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Supported by the Chaim Weizman Postdoctoral Fellowship.

Supported in part by NSF under grant No. MCS-8102448.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Linial, N., Saks, M. & Sós, V.T. Largest digraphs contained in alln-tournaments. Combinatorica 3, 101–104 (1983). https://doi.org/10.1007/BF02579345

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02579345

AMS subject classification (1980)

Search

Navigation