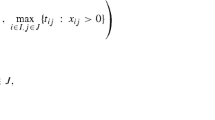Summary
An algorithm for the ranking of the feasible solutions of a bottleneck linear programming problem in ascending order of values of a concave bottleneck objective function is developed in this paper. The “best” feasible solution for a given value of the bottleneck objective is obtained at each stage. It is established that only the extreme points of a convex polytope need to be examined for the proposed ranking. Another algorithm, involving partitioning of the nodes, to rank the feasible solutions of the bottleneck linear programming problem is proposed, and numerical illustrations for both are provided.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bansal, S. and M. C. Puri (1980).A Min Max Problem. ZOR, Series A, vol. 24, Issue5, 191–200.
Bhatia, H. L., Kanti Swarup and M. C. Puri (1976).A Procedure for Time Minimization transportation Problem. Math. Operationsforsch. u. Statist.7, Heft 3, s. 395–403.
Francis, R.L. and J.A. White (1974).Facility layout and location: an analytical approach. Prentice Hall, Englewood Cliffs, N.J.
frieze, A.M. (1975).Bottleneck Linear Programming. Opl. Res. Q. Pergamon Press, vol. 26,4(ii), 871–874.
Garfinkel, R.S. (1970).An improved algorithm for the Bottleneck Assignment Problem. Working Paper Series no. 7003, College of Business Administration, University of Rochester, Rochester, New York.
Garfinkel, R.S. and M.R. Rao (1971).The Bottleneck Transportation Problem. Nav. Res. Log. Quart.18, 465–472.
Gross, O. (1959).The Bottleneck Assignment Problem, The RAND Corporation, P-1630.
Gupta, S.K. and A.K. Mittal (1982).A Min Max Problem as a linear programming problem, Opsearch, vol.19, no. 1, 49–53.
Hadley, G. (1962).Linear Programming, Addison-Wesley.
Hammer, P.L. (1969).Time Minimizing Transportation Problem, Nav Ras. log. Quart,16, 345–357.
Kaplan, S. (1974).Applications of programs with maximum objective functions to problems of optimal resource allocation. Operations Research22(4), 802–807.
Mangasarian, O. (1969). Non-Linear Programming, McGraw Hill.
Minoux, M. (1989).Solving Combinatorial Problems with combined mim-max min-sum objective and applications. Mathematical Programming45, 361–372.
Murty, K.G. (1968):An algorithm for ranking all the assignments in order of increasing cost, Operations Research16, 682–687.
Murty, K.G. (1976). Linear and Combinatorial Programming, Wiley, New York.
Satya Prakash. (1981).A Transportation Problem with objectives to minimize total cost and duration of trasportation, Opsearch, vol.18, no. 4.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Mathur, K., Puri, M.C. & Bansal, S. On ranking of feasible solutions of a bottleneck linear programming problem. Top 3, 265–283 (1995). https://doi.org/10.1007/BF02568589
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02568589