Inertial gravimetry—A comparison of Kalman filtering-smoothing and post-mission adjustment techniques

Abstract

The determination of the anomalous gravity vector by inertial techniques is critically dependent on the ability to separate system errors from gravity field effects. This separation should in principle be based on the characteristic difference of the two effects: system errors are a function of time, while gravity field variations are a function of position only. Factors such as vehicle speed thus have a direct influence on the ability to separate the two effects.

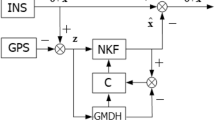
In practice, inertial gravimetry has been mainly based on Kalman filteringoptimal smoothing. In Kalman filtering the error separation is in principle obtained by using different effective correlation lengths for the system errors and the anomalous gravity field variations. The advantage of Kalman filtering is the good physical description of the instrument errors, but a serious drawback is the inability to account for spatial correlations, especially for the “identical” gravity field on forward-backward traverses. Optimal smoothing with gravimetric control at the two endpoints of the traverse will remove systematic biases but will not eliminate the problem mentioned above.

An alternative post-mission adjustment method has been developed with the explicit goal to utilize repeated zero velocity updates on the same points of the traverse. In this method, the major system errors are modelled by a few parameters related to the propagation of the initial state errors, with residual errors modelled by Markov processes. Gravity vectors are solved for simultaneously in a least-squares collocation adjustment, using simplified transition matrix elements to propagate the effects of the unknown gravity field.

Results of the two methods are evaluated and compared, using Ferranti data from a number of truck and helicopter traverses in the Kananaskis area west of Calgary. In this area of extreme gravity field variation, gravity anomalies can in general be determined to an accuracy of a few mgals with theFILS system, while deflections of the vertical are typically determined at the 1 arcsec level.