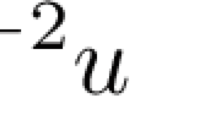Skip to main content
SpringerLink
Log in

K orbits, harmonic analysis, and equations integrable in a four-dimensional lie group

  • Elementary-particle Physics and Field Theory
  • Published:
Russian Physics Journal Aims and scope

Abstract

Harmonic analysis is performed for a resoluble four-dimensional Lie group, which is used to integrate linear differential equations that are not integrable within the theory of variable separation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. A. Kirillov, Representation Theory Elements [in Russian], Nauka, Moscow (1978).

    Google Scholar 

  2. A. A. Kirillov, “Introduction to representation theory and noncommutative harmonic analysis,” in: Surveys of Science and Engineering, Contemporary Fundamental Lines in Mathematics [in Russian], VINITI,22, 5–162 (1988).

  3. D. P. Zhelobenko and A. I. Shtern, Lie-Group Representations [in Russian], Nauka, Moscow (1983).

    Google Scholar 

  4. A. V. Shapovalov and I. V. Shirokov, Teor. Mat. Fiz.,104, No. 2, 195–213 (1995).

    MATH  MathSciNet  Google Scholar 

  5. A. S. Mishchenko and A. T. Fomenko, Proceedings of the Seminar on Vector and Tensor Analysis, Issue 20 [in Russian], Izd. Moscow Univ., Moscow (1981), pp. 5–54.

    Google Scholar 

  6. A. Baruth and R. Ronchka, Group Representation Theory and Its Applications [Russian translation], Mir, Moscow (1980).

    Google Scholar 

  7. V. N. Shapovalov, Diff. Uravneniya,16, No. 10, 1864–1874 (1980).

    MATH  MathSciNet  Google Scholar 

Download references

Authors
  1. S. I. Dianin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. V. Shirokov
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Omsk State University. Translated from Izvestiya Vysshikh Uchebnykh Zavedenii, Fizika, No. 10, pp. 90–96, October, 1998.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dianin, S.I., Shirokov, I.V. K orbits, harmonic analysis, and equations integrable in a four-dimensional lie group. Russ Phys J 41, 1033–1037 (1998). https://doi.org/10.1007/BF02514474

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02514474

Keywords

Search

Navigation