Abstract
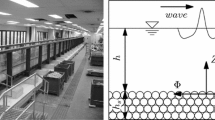
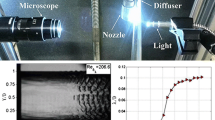
We present a theoretical basis for a direct method of determining buoyancy period (frequency) as a function of depth by registering the displacements and oscillations of the hydrodynamic wake formed in a stationary liquid by freely ascending bubbles (the density marker method). We achieve an error no greater than 5% by comparing theoretical computations of parameters for internal waves generated by a free submerged thin wake having uniform transverse density distribution in an exponentially stratified liquid with measurements of internal waves in the liquid. We find that there is a power law for the decrease in amplitude of internal oscillations with time.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. Krauss, Internal Waves [Russian translation], Gidrometeoizdat, Leningrad (1968).
Yu. S. Il'inykh, et al., Izmer. Tekh., No. 8, 39 (1995).
D. L. Boyer and L. Tao, J. Fluid Mech.,180, 429 (1987).
V. I. Nekrasov and Yu. D. Chashechkin, Metrologiya, No. 11, 36 (1974).
R. A. Hartunian and W. R. Sears, J. Fluid Mech.,3, 27 (1957).
Yu. D. Chashechkin, et al., “Simulation of internal structures and the dynamics of natural systems,” IPM RAN Preprint No. 592 (1997).
Yu. V. Kistovich and Yu. D. Chashechkin, PMM,59, No. 4, 607 (1995).
M. V. Fedoryuk, Asymptotics: Integrals and Series [in Russian], Nauka, Moscow (1987).
D. W. Kaufmann, Reinhold, New York (1960).
A. V. Gvozdev, V. I. Neklyudov, and Yu. D. Chashechkin, Izmer. Tekh., No. 3, 33 (1990).
Additional information
Translated from Imeritel'naya Tekhnika, No. 6, pp. 15–18, June, 1998.
Rights and permissions
About this article
Cite this article
Smirnov, S.A., Chashechkin, Y.D. & Il'inykh, Y.S. High-accuracy method for measuring profiles of buoyancy periods. Meas Tech 41, 514–519 (1998). https://doi.org/10.1007/BF02504319
Issue Date:
DOI: https://doi.org/10.1007/BF02504319