The surface seiches of Lake of Zürich

Abstract

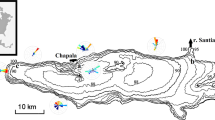
A computational analysis of the periods and structure of surface seiches of Lake of Zürich and its experimental verification from three simultaneous water gauge recordings, mounted along the shores in Zürich. Pfäffikon and Rapperswil is given. After a brief historical account the governing equations and the procedure, how they were discretized by a finite element technique are introduced. Computational results concern seiche periods and seiche structure, in particular co-range and co-tidal lines for the first seven free oscillations which are discussed in detail.

Experimental verification is from recordings taken during January 1982. Inspection by eye allows identification of the three lowest order seiche periods including the phase shift between the recordings of Zürich and Rapperswil. Higher order modes (up to order 19) are also detected by this method. Power spectral analysis including interstation phase shift and coherence allow identification of over fifteen seiche periods. Agreement between the theoretically predicted and experimentally determined periods is excellent for the first, second, third, fair for the fourth, fifth and sixth mode and good for the other higher modes, but statistical reliability is low for these.

Zusammefassung

Die Perioden und die Struktur der Oberflächenseiches des Zürichsees werden rechnerisch ermittelt und mittels dreier simultan arbeitender Pegel, die dem Ufer entlang bei Zürich, Pfäffikon und Rapperswil aufgebaut waren, bestätigt und erweitert. Nach einer kurzen, historischen Übersicht werden die Grundgleichungen und deren Approximation mit einer Finite-Element-Methode diskutiert. Die rechnerischen Resultate betreffen die Seicheperioden und die Seichestruktur, speziell die Linien konstanten Hubes und konstanter Phase für die sieben ersten freien Schwingungen, die im Detail diskutiert werden.

Die experimentelle Überprüfung erfolgt mit Zeitreihen vom Januar 1982. Deren Sichtung erlaubt, die drei Seiches mit den längsten Perioden von Auge zu isolieren samt den Phasendifferenzen zwischen den Messreihen von Zürich und Rapperswil. Eigenschwingungen höherer Ordnung (bis zur Ordnung 19) lassen sich mit dieser Methode ebenfalls angeben. Spektralanalysen, einschliesslich der Phasendifferenz und der Kohärenz aus Messreihenpaaren. erlauben eine Identifikation von mehr als 15 Seicheperioden. Die Übereinstimmung zwischen den rechnerisch vorausgesagten und den experimentell bestimmten Perioden ist für die Schwingungen der ersten, zweiten, dritten und siebten Ordnung ausgezeichnet, für die vierte, fünfte und sechste befriedigend und gut für die anderen höheren Seicheperioden, aber mit wenig statistischer Verlässlichkeit.

Résumé

Les périodes et la structure des seiches de surface du lac de Zurich sont calculées et vérifiées simultanément au moyen de trois jauges installées à Zurich. Pfäffikon et Rapperswil. Use brève introduction historique est suivie de la discussion des équations de base et de leur approximation au moyen d'une méthode à éléments finis. Les résultats des calculs concernent les périodes des seiches et leur structure, en particulier les lignes d'élévation constante et de phase constante pour les sept premières oscillations libres, qui sont discutées en détail.

La vérification expérimentale est effectuée au moyen d'enregistrements de seiches pendant le mois de janvier 1982. L'analyse visuelle permet d'identifier les trois seiches avec les plus longues périodes ainsi que les différences de phases entre les enregistrements de Zurich et de Rapperswil. Les oscillations d'ordre supérieur (jusqu'à 19) sont détectées de la même manière. Les analyses spectrales y compris la différence de phase et la cohérence permettent d'indentifier plus de 15 périodes de seiches. L'accord entre les périodes déterminées théoriquement et par mesure est excellent pour le premier, le deuxième et troisiéme, satisfaisant pour le quatrième, cinquième et sixième ordre et bon pour les ordres supérieurs avec moins de sécurité statistique pour ces derniers.